四川省绵阳市2023年中考二模数学试题

试卷更新日期：2023-05-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数﹣2023的绝对值是（）

A、2023 B、﹣2023 C、 $\frac{1}{2023}$ D、 $- \frac{1}{2023}$

查看试题解析
2. 芝麻被称为“八谷之冠”，是世界上最古老的油料作物之一．它作为食品和药物，得到广泛的使用．经测算，一粒芝麻的质量约为 $0.000 002 01$ kg，将100粒芝麻的质量用科学记数法表示约为（）

A、 $20.1 \times 10^{- 3}$ kg B、 $2.01 \times 10^{- 4}$ kg C、 $0.201 \times 10^{- 5}$ kg D、 $2.01 \times 10^{- 6}$ kg

查看试题解析
3. 下列各运算中，正确的运算是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、（2a）³＝8a³ C、a⁸÷a⁴＝a² D、（a-b）²＝a²-b²

查看试题解析
4. 如图，已知直线 $a ∥ b$ ，直角三角形顶点C在直线b上，且 $∠ A = 55 °$ ，若 $∠ 1 = 58 °$ ，则 $∠ 2$ 的度数是（）

A、 $35 °$ B、 $32 °$ C、 $38 °$ D、 $42 °$

查看试题解析
5. 如图， $D E$ 垂直平分 $A B$ ，交 $A B$ 于点E，交 $B C$ 于点D， $△ A C D$ 的周长是13， $B C = 8$ ，则 $A C$ 的长是（）

A、6 B、5 C、4 D、3

查看试题解析
6. 若关于 $x$ 的方程 $\frac{x}{x - 2} + \frac{a}{2 - x} = a$ 无解，则 $a$ 的值为（）

A、2 B、 $\frac{2}{3}$ C、1或2 D、2或 $\frac{2}{3}$

查看试题解析
7. 下面是某校八年级（2）班两组女生的体重（单位：kg）：
第1组35，36，38，40，42，42，75

第2组35，36，38，40，42，42，45

下面关于对这两组数据分析正确的是：（）

A、平均数、众数、中位数都相同 B、平均数﹑众数、中位数都只与部分数据有关 C、中位数相同，都是39 D、众数、中位数不受极端值影响，平均数受极端值影响

查看试题解析
8. 已知圆锥的三视图如图所示，则这个圆锥的侧面展开图的面积为（）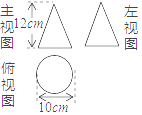

A、60πcm² B、65πcm² C、120πcm² D、130πcm²

查看试题解析
9. 如图，抛物线y=-x²+mx的对称轴为直线x=2，若关于x的一元二次方程-x²+mx-t=0 (t为实数)在l<x<3的范围内有解，则t的取值范围是（）

A、-5<t≤4 B、3<t≤4 C、-5<t<3 D、t>-5

查看试题解析
10. 若A，B，C是⊙O上三点， $∠ A B C = 150 ° ， A C = 6$ ，则⊙O的半径是（）

A、 $2 \sqrt{3}$ B、 $3 \sqrt{2}$ C、6 D、 $6 \sqrt{2}$

查看试题解析
11. 下列四个命题：①一组同旁内角相等的平行四边形是矩形；②对角线互相垂直且相等的四边形是正方形；③顺次连接菱形四边中点得到的四边形是矩形；④等边三角形既是轴对称图形又是中心对称图形．其中真命题共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 在矩形ABCD中，点P为CD边上一点(DP＜CP)，∠APB＝90°．将△ADP沿AP翻折得到△AD′P ， PD′的延长线交边AB于点M ，过点B作BN∥MP交DC于点N ，连接AC ，分别交PM ， PB于点E ， F．现有以下结论：①连接DD′，则AP垂直平分DD′；②四边形PMBN是菱形；③AD²＝DP⋅PC；④若AD＝2DP ，则 $\frac{E F}{A E} = \frac{5}{9}$ ．其中正确的结论的个数是（）

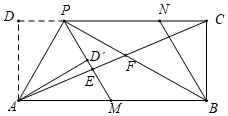A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 在实数范围内分解因式： $6 x^{2} y + 12 x y =$ ．

查看试题解析
14. 已知一元二次方程 $a x^{2} - x + 1 = 0 (a \neq 0)$ 有两个实数根，则a的取值范围是．

查看试题解析
15. 如图，点C为线段AB延长线上一点，正方形AEFG和正方形BCDE的面积分别为8和4，则△EDF的面积为．

查看试题解析
16. 若关于x的不等式组 ${\begin{array}{l} \frac{x - 2}{4} < \frac{x - 1}{3} \\ 2 x - m \leq 2 - x \end{array}$ 有且只有三个整数解，则m的取值范围是．

查看试题解析
17. 如图，菱形 ABCD 中，∠D = 120°，AB = 4，点 E 为 BC 的中点，点 P 为对角线 AC 上的任意一点，连接 PB，PE，则 PB + PE 的最小值为．

查看试题解析
18. 在平面直角坐标系中，直线y＝﹣x与双曲线y＝﹣ $\frac{k^{2} + 1}{x}$ 交于点A（x₁ ， y₁），B（x₂ ， y₂），则x₁﹣y₂的值为.

查看试题解析

三、解答题

19.

(1)、计算： $\sqrt{8} + {(\frac{1}{3})}^{- 2} - | 1 - \sqrt{2} | - 2 c o s 45 °$ ．

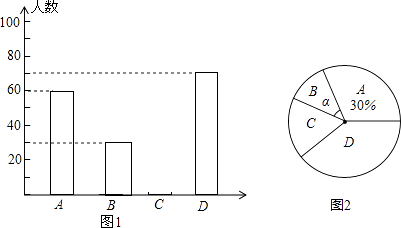
(2)、先化简，再求值： $\frac{x - 2}{x^{2} - 4 x + 4} \div (x + 2 - \frac{x^{2} + x - 4}{x - 2}) + \frac{1}{x + 1}$ ，其中 $x^{2} + x - 5 = 0$ ．

查看试题解析
20. 黔东南州某中学为了解本校学生平均每天的课外学习实践情况，随机抽取部分学生进行问卷调查，并将调查结果分为A，B，C，D四个等级，设学生时间为t（小时），A：t＜1，B：1≤t＜1.5，C：1.5≤t＜2，D：t≥2，根据调查结果绘制了如图所示的两幅不完整的统计图．请你根据图中信息解答下列问题：

(1)、本次抽样调查共抽取了多少名学生？并将条形统计图补充完整；

(2)、本次抽样调查中，学习时间的中位数落在哪个等级内？

(3)、表示B等级的扇形圆心角α的度数是多少？

(4)、在此次问卷调查中，甲班有2人平均每天课外学习时间超过2小时，乙班有3人平均每天课外学习时间超过2小时，若从这5人中任选2人去参加座谈，试用列表或化树状图的方法求选出的2人来自不同班级的概率．

查看试题解析
21. 如图，一座山的一段斜坡BD的长度为600米，且这段斜坡的坡度i=1：3（沿斜坡从B到D时，其升高的高度与水平前进的距离之比）．已知在地面B处测得山顶A的仰角为33°，在斜坡D处测得山顶A的仰角为45°．求山顶A到地面BC的高度AC是多少米？（结果用含非特殊角的三角函数和根式表示即可）

查看试题解析

22. 某家具商场计划购进某种餐桌、餐椅进行销售，有关信息如下表：

	原进价（元/张）	零售价（元/张）	成套售价（元/套）
餐桌	a	380	940
餐椅	$a - 140$	160	940

已知用600元购进的餐椅数量与用1300元购进的餐桌数量相同．

(1)、求表中a的值；

(2)、该商场计划购进餐椅的数量是餐桌数量的5倍还多20张，且餐桌和餐椅的总数量不超过200张．若将一半的餐桌成套（一张餐桌和四张餐椅配成一套）销售，其余餐桌、餐椅以零售方式销售，请问怎样进货，才能获得最大利润？最大利润是多少？

查看试题解析

23. 如图，已知AB是⊙O的直径，D是⊙O上一点，连接OD，BD，C为AB延长线上一点，连接CD，且∠BDC= $\frac{1}{2}$ ∠BOD．

(1)、求证：CD是⊙O的切线；

(2)、若⊙O的半径为2，CD $= \sqrt{5}$ ，求BC和BD的长．

查看试题解析
24. 已知，在Rt△ABC中， $∠ B A C = 90 °$ ， $A H ⊥ B C$ 于点H，P是 $A B$ 上一动点， $A D ⊥ C P$ ， $B E ⊥ C P$ ， $H D$ 与 $B E$ 两延长线交于点F．

(1)、如图①，当 $A B = A C$ 时，求 $∠ B F H$ 的度数．

(2)、如图②，当 $∠ A B C = 30 °$ 时，探求 $B F$ 与 $C D$ 的数量关系，说明理由．

(3)、当 $∠ A B C = α$ 时，直接用 $α$ 的代数式表示 $\frac{C D}{B F}$ 的值．

查看试题解析
25. 如图，在平面直角坐标系中，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图像与x轴相交于A，B两点，与y轴交于点C，已知点 $A (1 ， 0)$ ，点 $C (0 ， 3)$ ，且 $B C = 5$ ．

(1)、求二次函数的解析式；

(2)、若点D的坐标为 $(- \frac{9}{4} ， 0)$ ，试判断 $△ D C B$ 的形状，并说明理由；

(3)、在抛物线的对称轴上是否存在点P，使得以B，C，P为顶点的三角形是直角三角形？若存在，请求出点P的坐标：若不存在，请说明理由

查看试题解析