四川省泸州市江阳区2023年中考一模数学试题
试卷更新日期:2023-05-23 类型:中考模拟
一、单选题
-
1. 3的算术平方根是( )A、 B、 C、 D、92. 2023年3月18日上午,重庆至昆明高速铁路重庆至宜宾段控制性工程——泸州沱江特大桥主跨实现合龙.泸州沱江特大桥全长约2613米,为国内高速铁路首次采用双柱式V型桥塔、空间扇形索面斜拉索的斜拉桥,请将2613用科学记数法表示( )A、 B、 C、 D、3. 下列各式计算正确的是( )A、 B、 C、 D、4. 如图是某几何体的三视图,该几何体是( )
 A、三棱柱 B、长方体 C、圆锥 D、圆柱5. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、6. 如图,已知 , 点E(不与点A,点D重合)在线段上,连接 , 若 , , 则( )
A、三棱柱 B、长方体 C、圆锥 D、圆柱5. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、6. 如图,已知 , 点E(不与点A,点D重合)在线段上,连接 , 若 , , 则( ) A、 B、 C、 D、7. 有五张背面完全相同的卡片,正面分别写有数字1,2,3,4,5,把这些卡片背面朝上洗匀后,从中随机抽取一张,其正面的数字是奇数的概率为( )A、 B、 C、 D、8. 如图,分别以的顶点A和B为圆心,大于长为半径画弧,两弧相交于点M,N.作直线 , 交于点D,交于点E,连接 . 若 , 则的周长为( )
A、 B、 C、 D、7. 有五张背面完全相同的卡片,正面分别写有数字1,2,3,4,5,把这些卡片背面朝上洗匀后,从中随机抽取一张,其正面的数字是奇数的概率为( )A、 B、 C、 D、8. 如图,分别以的顶点A和B为圆心,大于长为半径画弧,两弧相交于点M,N.作直线 , 交于点D,交于点E,连接 . 若 , 则的周长为( ) A、7 B、9 C、 D、9. 如图,菱形的对角线相交于点O,过点D作于点E,连接 , 若菱形的面积为 , , 则的长为( )
A、7 B、9 C、 D、9. 如图,菱形的对角线相交于点O,过点D作于点E,连接 , 若菱形的面积为 , , 则的长为( ) A、3 B、 C、 D、210. 关于x的一元二次方程有实数根,则a的取值范围是( )A、 B、 C、且 D、且11. 如图,矩形的对角线相交于点O, , 分别过点D,点C作的平行线,两线相交于点E,连接交于点F,则的值是( )
A、3 B、 C、 D、210. 关于x的一元二次方程有实数根,则a的取值范围是( )A、 B、 C、且 D、且11. 如图,矩形的对角线相交于点O, , 分别过点D,点C作的平行线,两线相交于点E,连接交于点F,则的值是( )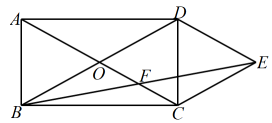 A、7 B、 C、8 D、12. 在平面直角坐标系中,抛物线上的两点 , , 若对于 , 都有 , 则m的取值范围是( )A、或 B、 C、或 D、
A、7 B、 C、8 D、12. 在平面直角坐标系中,抛物线上的两点 , , 若对于 , 都有 , 则m的取值范围是( )A、或 B、 C、或 D、二、填空题
-
13. 若分式 的值为 ,则 的值为.14. 分解因式: =.15. 若一个直角三角形两条直角边的长分别是一元二次方程的两个实数根,则这个直角三角形斜边的长是 .16. 如图,在平面直角坐标系中,已知点 , C为平面内的动点,且满足 , D为直线上的动点,则线段长的最小值为 .

三、解答题
-
17. 计算: .18. 计算: .19. 如图,在中,E,G,H,F分别是上的点,且 . 求证: .
 20. 某校开展“爱读书、读好书、善读书”的阅读活动,随机抽取了m名学生参加“平均每周课外阅读时间”的调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.请根据图表中的信息解答下列问题:
20. 某校开展“爱读书、读好书、善读书”的阅读活动,随机抽取了m名学生参加“平均每周课外阅读时间”的调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.请根据图表中的信息解答下列问题:组别
时间/小时
频数/人数
A组
4
B组
n
C组
10
D组
18
E组
8
F组
4
 (1)、m= , n=;(2)、若该校有400人,试估计全校“平均每周课外阅读时间”在范围的学生人数;(3)、已知F组的学生中,只有1名男生,其余都是女生,用列举法求以下事件的概率:从F组中随机选取2名学生,恰好都是女生.21. 某校将举行跳绳比赛,需要购买A、B两种跳绳.已知每根A种跳绳的单价比B种跳绳的单价少5元,300元购买A种跳绳的数量与450元购买B种跳绳的数量相等.(1)、求购进一根A种跳绳和一根B种跳绳各需多少元?(2)、设购买A种跳绳m根,若学校计划购买A,B两种跳绳共45根,且购买A种跳绳的数量不超过B种跳绳的数量的2倍,请设计出最省钱的购买方案.22. 如图,在平面直角坐标系中,一次函数的图像与反比例函数的图像相交于 , 两点.
(1)、m= , n=;(2)、若该校有400人,试估计全校“平均每周课外阅读时间”在范围的学生人数;(3)、已知F组的学生中,只有1名男生,其余都是女生,用列举法求以下事件的概率:从F组中随机选取2名学生,恰好都是女生.21. 某校将举行跳绳比赛,需要购买A、B两种跳绳.已知每根A种跳绳的单价比B种跳绳的单价少5元,300元购买A种跳绳的数量与450元购买B种跳绳的数量相等.(1)、求购进一根A种跳绳和一根B种跳绳各需多少元?(2)、设购买A种跳绳m根,若学校计划购买A,B两种跳绳共45根,且购买A种跳绳的数量不超过B种跳绳的数量的2倍,请设计出最省钱的购买方案.22. 如图,在平面直角坐标系中,一次函数的图像与反比例函数的图像相交于 , 两点. (1)、求该反比例函数的表达式;(2)、过点A作直线 , 交该反比例函数图象于另一点C,交y轴于点D、连接 , 若 , 求的长.23. 为了计算花园中古树P到公路l的距离,某数学兴趣小组在公路l上的点A处,测得古树P在东北方向;从A处向正东方向行走30米,到达公路l上的点B处,再次测得古树P在北偏东的方向上,求古树P到公路l的距离.(结果保留整数,参考数据:)
(1)、求该反比例函数的表达式;(2)、过点A作直线 , 交该反比例函数图象于另一点C,交y轴于点D、连接 , 若 , 求的长.23. 为了计算花园中古树P到公路l的距离,某数学兴趣小组在公路l上的点A处,测得古树P在东北方向;从A处向正东方向行走30米,到达公路l上的点B处,再次测得古树P在北偏东的方向上,求古树P到公路l的距离.(结果保留整数,参考数据:) 24. 如图,是的直径,点C是外一点,点D在上,且 , 连接交于点E.过点E作于点H,交于点G,交于点F,且 .
24. 如图,是的直径,点C是外一点,点D在上,且 , 连接交于点E.过点E作于点H,交于点G,交于点F,且 . (1)、猜想与的位置关系,并证明;(2)、连接 , 若 , , 求的长和的半径.25. 1.如图,在平面直角坐标系中,抛物线经过点 , 点 . 直线交x轴于点C,点P是直线下方抛物线上的一个动点.
(1)、猜想与的位置关系,并证明;(2)、连接 , 若 , , 求的长和的半径.25. 1.如图,在平面直角坐标系中,抛物线经过点 , 点 . 直线交x轴于点C,点P是直线下方抛物线上的一个动点. (1)、求该抛物线的函数表达式;(2)、过点P作于点D,轴,交于点E.当的周长取得最大值时,求点P的坐标和的周长的最大值;(3)、已知点P为(2)中求得的点P,点M是该抛物线上一点,点N是该抛物线对称轴上一点,直接写出所有使得以点P,B,M,N为顶点的四边形是平行四边形的点M的坐标,并把其中一个求点M的坐标的解答过程写出来.
(1)、求该抛物线的函数表达式;(2)、过点P作于点D,轴,交于点E.当的周长取得最大值时,求点P的坐标和的周长的最大值;(3)、已知点P为(2)中求得的点P,点M是该抛物线上一点,点N是该抛物线对称轴上一点,直接写出所有使得以点P,B,M,N为顶点的四边形是平行四边形的点M的坐标,并把其中一个求点M的坐标的解答过程写出来.