四川省广元市苍溪县2023年中考一模数学试题
试卷更新日期:2023-05-23 类型:中考模拟
一、单选题
-
1. 的绝对值是( )A、 B、5 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图所示的几何体,其左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 某校举行党史知识竞赛,10名参加决赛选手成绩统计如下:
4. 某校举行党史知识竞赛,10名参加决赛选手成绩统计如下:成绩(分)
94
95
97
98
100
选手(个)
1
2
2
4
1
这10名参加决赛选手成绩(分)的中位数和众数分别是( )
A、97,98 B、 , 98 C、98,98 D、98,5. 《九章算术》中有问题:1亩好田是300元,7亩坏田是500元,一人买了好田坏田一共是100亩,花费了10000元,问他买了多少亩好田和坏田?设一亩好田为x元,一亩坏田为y元,根据题意列方程组得( )A、 B、 C、 D、6. 如图,为的直径,是的弦,、的延长线交于点E,已知 , , 则的度数为( ) A、 B、 C、 D、7. 已知关于x的方程的一个解与方程的解相同,则方程的另一个解是( )A、 B、 C、 D、8. 如图,把边长为的正方形绕点A顺时针旋转得到正方形 , 边与交于点O,则四边形 的周长是( )
A、 B、 C、 D、7. 已知关于x的方程的一个解与方程的解相同,则方程的另一个解是( )A、 B、 C、 D、8. 如图,把边长为的正方形绕点A顺时针旋转得到正方形 , 边与交于点O,则四边形 的周长是( ) A、 B、 C、 D、9. 如图,已知正方形边长为3,点E在边上且 , 点P,Q分别是边 , 的动点(均不与顶点重合),当四边形的周长取最小值时,四边形的面积是( )
A、 B、 C、 D、9. 如图,已知正方形边长为3,点E在边上且 , 点P,Q分别是边 , 的动点(均不与顶点重合),当四边形的周长取最小值时,四边形的面积是( )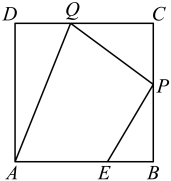 A、 B、 C、 D、10. 如图,抛物线与x轴交于点 , 顶点坐标为 , 与y轴的交点在和两点之间(不包含端点).下列结论中:①;②;③;④一元二次方程的两个根分别为 , . 正确的个数有( )
A、 B、 C、 D、10. 如图,抛物线与x轴交于点 , 顶点坐标为 , 与y轴的交点在和两点之间(不包含端点).下列结论中:①;②;③;④一元二次方程的两个根分别为 , . 正确的个数有( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 据报道,生命科学家开发出一项突破性的技术,只要把所需要的尺寸输入电脑,就能培养出完全符合要求的肌体组织或骨骼,而所使用的材料每层只有0.0012厘米厚,这个数用科学记数法表示应为厘米.12. 分解因式:.13. 如图,在中, , , 以点A为圆心,适当长度为半径画弧分别交、于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结并延长交于点D,则下列说法:①是的平分线;②;③是等腰三角形;④点D到直线的距离等于的长度.其中正确的有 . (填序号)
 14. 已知 , 则的值为 .15. 已知一元二次方程有两个相等的实数根,点、是反比例函数上的两个点,若 , 则(填“”或“”或“”).16. 如图,线段为的直径,点C在的延长线上, , , 点P是上一动点,连接 , 以为斜边在的上方作Rt , 且使 , 连接 , 则长的最大值为 .
14. 已知 , 则的值为 .15. 已知一元二次方程有两个相等的实数根,点、是反比例函数上的两个点,若 , 则(填“”或“”或“”).16. 如图,线段为的直径,点C在的延长线上, , , 点P是上一动点,连接 , 以为斜边在的上方作Rt , 且使 , 连接 , 则长的最大值为 .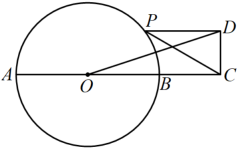
三、解答题
-
17. 计算: .18. 先化简: , 其中x是不等式的整数解,选取你认为合适的x的值代入求值.19. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,过点A作AE⊥BD,垂足为点E,过点C作CF⊥BD,垂足为点F.
 (1)、求证:AE=CF;(2)、若∠AOE=70°,∠EAD=3∠EAO,求∠BCA的度数.20. “校园安全”受到全社会的广泛关注,卧龙中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了两幅尚不完整的统计图,如图所示,请根据统计图中所提供的信息解答下列问题:
(1)、求证:AE=CF;(2)、若∠AOE=70°,∠EAD=3∠EAO,求∠BCA的度数.20. “校园安全”受到全社会的广泛关注,卧龙中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了两幅尚不完整的统计图,如图所示,请根据统计图中所提供的信息解答下列问题: (1)、接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为度;(2)、请补全条形统计图;(3)、若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.21. 如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌 . 小明在山坡的坡脚A处测得宣传牌底部D的仰角为 , 沿山坡向上走到B处测得宣传牌顶部C的仰角为 . 已知山坡的坡度 , 米,米,求这块宣传牌的高度.(测角器的高度忽略不计,结果精确到米.参考数据: , )
(1)、接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为度;(2)、请补全条形统计图;(3)、若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.21. 如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌 . 小明在山坡的坡脚A处测得宣传牌底部D的仰角为 , 沿山坡向上走到B处测得宣传牌顶部C的仰角为 . 已知山坡的坡度 , 米,米,求这块宣传牌的高度.(测角器的高度忽略不计,结果精确到米.参考数据: , ) 22. 如图,一次函数的图象经过、两点,与反比例函数的图象在第一象限内的交于点M,若的面积为 .
22. 如图,一次函数的图象经过、两点,与反比例函数的图象在第一象限内的交于点M,若的面积为 . (1)、求一次函数和反比例函数的表达式;(2)、在x轴上是否存在点P,使?若存在,求出点P的坐标;若不存在,说明理由.23. 某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)、求一次函数和反比例函数的表达式;(2)、在x轴上是否存在点P,使?若存在,求出点P的坐标;若不存在,说明理由.23. 某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)、求A、B型号衣服进价各是多少元?(2)、若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.24. 如图,四边形ABCD中,∠B=∠C=90°,点E为BC中点,AE⊥DE于点E.点O是线段AE上的点,以点O为圆心,OE为半径的⊙O与AB相切于点G,交BC于点F,连接OG.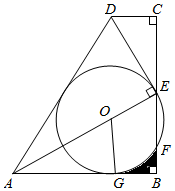 (1)、求证:△ECD∽△ABE;(2)、求证:⊙O与AD相切;(3)、若BC=6,AB=3 ,求⊙O的半径和阴影部分的面积.25. 【问题探究】
(1)、求证:△ECD∽△ABE;(2)、求证:⊙O与AD相切;(3)、若BC=6,AB=3 ,求⊙O的半径和阴影部分的面积.25. 【问题探究】 (1)、如图1,在菱形中, , 于点F, , 与交于点N,则的长为;(2)、如图2,点M是正方形对角线上的动点,连接于点H,连接 . 若 , 在M点从C到A的运动过程中,求的最小值;(3)、【问题解决】
(1)、如图1,在菱形中, , 于点F, , 与交于点N,则的长为;(2)、如图2,点M是正方形对角线上的动点,连接于点H,连接 . 若 , 在M点从C到A的运动过程中,求的最小值;(3)、【问题解决】
如图3,某市欲规划一块形如矩形的休闲旅游观光区,其中米,米,点E、F是观光区的两个入口(点E、F分别为的中点),P,Q分别在线段上,设计者欲从P到Q修建绿化带 , 从B到H修建绿化带 , 绿化带宽度忽略不计,且满足 , 点H在上, . 为了方便市民游览,计划从D到H修建观光通道 , 根据设计要求,请你帮助设计者求出观光通道的最小值.26. 如图,抛物线y=-x2+bx+c与x轴相交于A(-1,0),B(5,0)两点.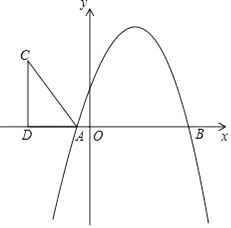 (1)、求抛物线的解析式;(2)、在第二象限内取一点C,作CD垂直x轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(1)、求抛物线的解析式;(2)、在第二象限内取一点C,作CD垂直x轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)、在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.