四川省成都市温江区2023年中考二模数学试题

试卷更新日期：2023-05-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 中国新能源汽车发展迅速，下列各图是国产新能源汽车图标，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 第31届世界大学生夏季运动会（简称大运会）将于2023年7月28日至8月8日在成都举行．成都东安湖体育公园主体育场将承担大运会开幕式，该场馆为建筑面积约320000平方米的大型甲级体育场，将320000用科学记数法表示为（）

A、 $3.2 \times 1 0^{4}$ B、 $3.2 \times 1 0^{6}$ C、 $3.2 \times 1 0^{5}$ D、 $32 \times 1 0^{6}$

查看试题解析
3. 下列计算正确的是（）

A、 $2 m - m = 1$ B、 ${(m^{3})}^{2} = m^{5}$ C、 ${(a + b)}^{2} = a^{2} + b^{2}$ D、 $(a + b) (a - b) = a^{2} - b^{2}$

查看试题解析
4. 如图， $A B ∥ C D$ ， $E F ⊥ A B$ 于点E， $E F$ 交 $C D$ 于点F， $E M$ 交 $C D$ 于点M，已知 $∠ 1 = 57 °$ ， $∠ 2$ 的度数为（）

A、 $43 °$ B、 $57 °$ C、 $33 °$ D、 $123 °$

查看试题解析
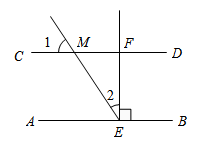5. 若点 $P$ 在第二象限，且到 $x$ 轴的距离是3，到 $y$ 轴的距离是1，则点 $P$ 的坐标是（）

A、 $(3 ， 1)$ B、 $(- 1 ， 3)$ C、 $(- 1 ， - 3)$ D、 $(- 3 ， 1)$

查看试题解析

6. 在学校的体考训练中，王华投掷实心球的7次成绩如下表所示，则这7次成绩的中位数是（）

次数	1	2	3	4	5	6	7
成绩/米	$9.7$	$9.6$	$9.8$	10	$9.8$	$9.9$	$10.1$

A、

9.6

米 B、

9.7

米 C、

9.8

米 D、

9.9

米

查看试题解析

7. 随着退林复耕的全面推进，成都天府绕城生态公园也在向十万亩良田公园变身．其中有两块面积相同的良田公园作为小麦试验田，第一块使用原品种，第二块使用新品种，分别收获小麦12000 $k g$ 和14000 $k g$ ，已知第一块试验田每公顷的产量比第二块少1500 $k g$ ．如果设第一块试验田每公顷的产量为x $k g$ ，请列出关于的x分式方程（）

A、 $\frac{12000}{x} = \frac{14000}{x + 1500}$ B、 $\frac{14000}{x} = \frac{12000}{x + 1500}$ C、 $\frac{x}{12000} = \frac{x + 1500}{14000}$ D、 $\frac{x}{14000} = \frac{x + 1500}{12000}$

查看试题解析
8. 某市新建一座景观桥．如图，桥的拱肋 $A D B$ 可视为抛物线的一部分，桥面 $A B$ 可视为水平线段，桥面与拱肋用垂直于桥面的杆状景观灯连接，拱肋的跨度 $A B$ 为40米，桥拱的最大高度 $C D$ 为16米（不考虑灯杆和拱肋的粗细），则与 $C D$ 的距离为5米的景观灯杆 $M N$ 的高度为（）

A、13米 B、14米 C、15米 D、16米

查看试题解析

二、填空题

9. 若a，b互为相反数，则 ${(a + b)}^{2} =$ ．

查看试题解析
10. 分解因式： $3 x + x^{3} =$ ．

查看试题解析
11. 已知一次函数 $y = k x + 3$ 的图象如图所示，则k= ．

查看试题解析
12. 如图，已知 $A B$ 是 $⊙ O$ 的弦， $∠ A O B = 140 °$ ， $O D ⊥ A B$ ，垂足为C，交 $⊙ O$ 于点D，若P为 $⊙ O$ 上一点，连接 $A P$ 、 $D P$ ，则 $∠ A P D$ 的度数是．

查看试题解析
13. 如图，在 $△ A B C$ 中，通过尺规作图，得到直线 $D E$ 和射线 $A F$ ，仔细观察作图痕迹，若 $∠ B = 43 °$ ， $∠ C = 50 °$ ，则 $∠ E A F =$ $°$ ．

查看试题解析

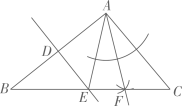
三、解答题

14.

(1)、计算： ${(\frac{1}{3})}^{- 1} + 2 s i n 60 ° - \sqrt{12} + | 1 - \sqrt{3} |$ ．

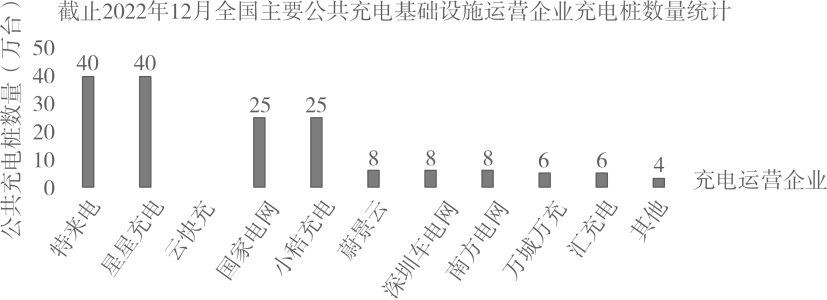
(2)、解不等式组： ${\begin{array}{l} 4 x - 2 \leq 3 (x + 1) \\ 1 - \frac{x - 1}{2} < \frac{x}{2} \end{array}$

查看试题解析
15. 随着人们对新能源汽车的认可，新能源汽车公共充电桩的需求量逐渐增大．根据某情报网信息：截止2022年12月，“特来电”“星星充电”“云快充”国家电网“等企业在全国投放公共充电桩的数量如图所示，其中“星星充电”市场份额为 $20 %$ ．

■公共充电缸数量（万台）

请根据图中信息，解答下列问题：

(1)、截止2022年12月全国主要公共充电基础设施运营商充电桩总数约为万台．

(2)、“云快充”的公共充电桩数量为万台，“云快充”的公共充电桩的市场份额为 %，请将统计图中“云快充”的公共充电桩数量补充完整并在图中标注出该企业充电桩数量.

(3)、王鹏收集到下列四个企业的图标，并将其制成编号分别为A，B，C，D的四张卡片（除编号和内容外，其余部分完全相同），将四张卡片背面朝上洗匀，放在桌面上，从中任意抽取一张，不放回，再抽取一张．请你用列表或画树状图的方法，求抽取到的两张卡片恰好是“A”和“D”的概率．

查看试题解析
16. 如图1是一个新款水杯，水杯不盛水时按如图2所示的位置放置，这样可以快速晾干杯底，干净透气：将图2的主体部分的抽象成图3，此时杯口与水平直线的夹角 $35 °$ ，四边形 $A B C D$ 可以看作矩形，测得 $A B = 10 c m$ ， $B C = 8 c m$ ，过点A作 $A F ⊥ C E$ ，交 $C E$ 于点F．求点A到水平直线 $C E$ 的距离 $A F$ 的长（结果精确到 $1 c m$ ， $s i n 35 ° \approx 0.5736$ ， $c o s 35 ° \approx 0.8192$ ， $t a n 35 ° \approx 0.7002$ ）

查看试题解析
17. 如图， $A B$ 是 $⊙ O$ 的直径，C是 $⊙ O$ 上一点， $∠ A C B$ 的平分线交 $A B$ 于E，交 $⊙ O$ 于 $D$ ，连接 $A D$ ， $B D$ ．

(1)、求证： $A D = B D$ ：

(2)、若 $A B = 4$ ， $A C = 1$ ，求 $\frac{C E}{E D}$ 的值．

查看试题解析
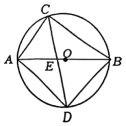18. 如图，在平面直角坐标系中，将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，点C坐标为（-1，0），点A的坐标为（0，2），一次函数 $y = k x + b$ 的图象经过点B，C，反比例函数 $y = \frac{m}{x}$ 图象也经过点B．

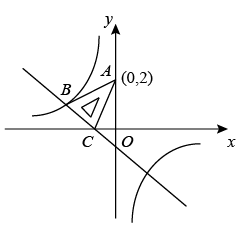(1)、求反比例函数的关系式；

(2)、直接写出当x<0时， $k x + b － \frac{m}{x} < 0$ 的解集．

(3)、若P是y轴正半轴一点，当△ACP是等腰三角形时，求出点P的坐标．

查看试题解析

四、填空题

19. 若 $m + n = 2$ ，那么代数式 $(\frac{2 m + n}{m^{2} - m n} + \frac{1}{m}) \cdot (m^{2} - n^{2})$ 的值为．．

查看试题解析
20. 一个三角形的两边长分别为3和9，第三边的长为一元二次方程 $x^{2} - 14 x + 48 = 0$ 的一个根，则这个三角形的周长为．

查看试题解析
21. 学习电学知识后，小婷同学用四个开关 $A 、 B 、 C 、 D$ ，一个电源和一个灯泡设计了一个电路图，现任意闭合其中两个开关，则小灯泡发光的概率等于．

查看试题解析
22. 如图，在 $△ A B C$ 中，点D、E分别是边AB、AC的中点，DF过EC的中点G并与BC的延长线交于点F，BE与DF交于点O．若 $△ A D E$ 的面积为S，则四边形BOGC的面积=

查看试题解析
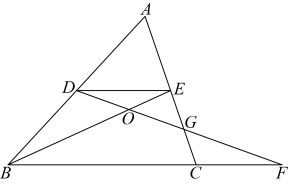23. 二次函数f（x）的图象开口向上，D为顶点，与x轴交于A，B两点，与y轴交于点C，若三角形ABC外接圆与y轴相切，且∠DAC＝150°，则x≠0时， $\frac{f (x)}{| x |}$ 的最小值是．

查看试题解析

五、解答题

24. 经过一年多的精准帮扶，王二家的网络商店（简称网店）将红枣、小米等优质土特产迅速销往全国．王二家网店中红枣和小米这两种商品的相关信息如下表：

商品	红枣	小米
规格	$1 k g /$ 袋	$2 k g /$ 袋
成本（元/袋）	45	44
售价（元/袋）	60	54

根据上表提供的信息，解答下列问题：

(1)、已知今年前五个月，王二家网店销售上表中规格的红枣和小米共4000

k g

，获得利润

4.2

万元，求这前五个月王二家网店销售这种规格的红枣多少袋：

(2)、根据之前的销售情况，估计今年6月到10月这后五个月，王二家网店还能销售上表中规格的红枣和小米共3000kg，其中，这种规格的红枣的销售量不低于600kg．假设这后五个月，销售这种规格的红枣为x（kg），销售这种规格的红枣和小米获得的总利润为y（元），求出y与x之间的函数关系式，并求这后五个月，王二家网店销售这种规格的红枣和小米至少获得总利润多少元．

查看试题解析

25. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + 2 x + c$ 与x轴分别交于点A(1，0)和点B，与y轴交于点C(0，﹣3)，连接BC．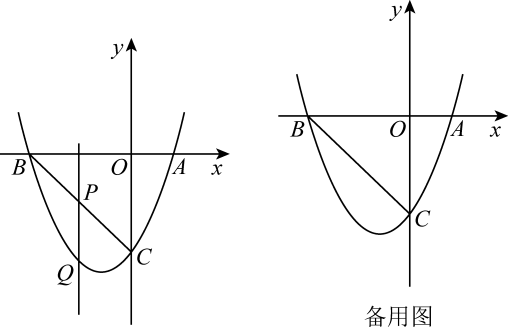

(1)、求抛物线的解析式及点B的坐标．

(2)、如图，点P为线段BC上的一个动点（点P不与点B，C重合），过点P作y轴的平行线交抛物线于点Q，求线段PQ长度的最大值．

(3)、动点P以每秒 $\sqrt{2}$ 个单位长度的速度在线段BC上由点C向点B运动，同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动，在平面内是否存在点N，使得以点P，M，B，N为顶点的四边形是菱形？若存在，请直接写出符合条件的点N的坐标；若不存在，请说明理由．

查看试题解析
26. 已知，矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．

(1)、如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长；

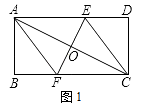(2)、如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，
①已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．
②若点P、Q的运动路程分别为a、b（单位：cm，ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，求a与b满足的数量关系式．

查看试题解析