陕西省西安市经开区2023年九年级中考数学联考模拟卷
试卷更新日期:2023-05-23 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 下列感冒胶囊的标识图中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 在我国《“十四五”就业促进规划》中明确提出,到2025年,城镇新增就业5500万人以上,数据5500万用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,正比例函数与一次函数的图象交于点 , 则关于x的不等式解集为( )
3. 在我国《“十四五”就业促进规划》中明确提出,到2025年,城镇新增就业5500万人以上,数据5500万用科学记数法表示为( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,正比例函数与一次函数的图象交于点 , 则关于x的不等式解集为( ) A、 B、 C、 D、6. 如图,点A,B,C均在上,若 , 则的度数是( )
A、 B、 C、 D、6. 如图,点A,B,C均在上,若 , 则的度数是( )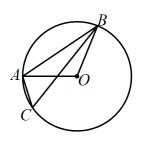 A、 B、 C、 D、7. 如图,在中, , , , D,F分别是 , 边的中点,于点E.连接 , 则的长为( )
A、 B、 C、 D、7. 如图,在中, , , , D,F分别是 , 边的中点,于点E.连接 , 则的长为( ) A、2 B、3 C、 D、8. 在抛物线(m为常数)上有三点 , , , 则 , , 三者之间的大小关系是( )A、 B、 C、 D、
A、2 B、3 C、 D、8. 在抛物线(m为常数)上有三点 , , , 则 , , 三者之间的大小关系是( )A、 B、 C、 D、二、填空题
-
9. 比较大小:3 . (填“>”“ <”或“=”)10. 若n边形的内角和是它的外角和的2倍,则n=.11. 相传大禹时期,洛阳市西洛宁县河中浮出神龟,背驮“洛书”,献给大禹,大禹依此治水成功,遂划天下为九州.图1是我国古代传说中的洛书,图2是洛书的数字表示,洛书是一个三阶幻方,就是将已知的9个数填入的方格中,使每一行、每一竖列以及两条斜对角线上的数字之和都相等.在图3的幻方中也有类似于图1的数字之和的这个规律,则m-n的值为 .
 12. 如图,正方形的边在x轴上,反比例函数的图象经过点A和边上点E,若正方形的边长为6, , 则k的值是 .
12. 如图,正方形的边在x轴上,反比例函数的图象经过点A和边上点E,若正方形的边长为6, , 则k的值是 . 13. 如图,在中, , , 平分 , 则的值是 .
13. 如图,在中, , , 平分 , 则的值是 .
三、解答题
-
14. 计算: .15. 解不等式组: .16. 化简: .17. 如图,在矩形中,请用尺规作一条直线 , 交于点E,交于点F,使得矩形沿直线折叠后,点B与点D重合.(保留作图痕迹,不写作法,标明字母)
 18. 如图,点E,C分别在边 , 上,已知 , . 求证: .
18. 如图,点E,C分别在边 , 上,已知 , . 求证: . 19. 如图,在平面直角坐标系中,的顶点都在格点(网格线的交点)上, .
19. 如图,在平面直角坐标系中,的顶点都在格点(网格线的交点)上, . (1)、将向右平移7个单位长度,再向下平移3个单位长度得到 , 画出平移后的 .(2)、点的坐标为 .20. 西安钟楼位于西安市中心,明城墙内东西南北四条大街的交汇处,为中国现存钟楼中形制最大、保存最完整的一座.如图,小琪想要测出钟楼的高度,于是在地面上的C处放置了一面镜子,当他站在离镜子C处的E处时,恰好从镜子里看到钟楼顶端A在镜子中的像(即).已知B,C,E在同一直线上,小琪的眼睛离地面的高度 , , 求钟楼的高度.
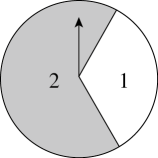
(1)、将向右平移7个单位长度,再向下平移3个单位长度得到 , 画出平移后的 .(2)、点的坐标为 .20. 西安钟楼位于西安市中心,明城墙内东西南北四条大街的交汇处,为中国现存钟楼中形制最大、保存最完整的一座.如图,小琪想要测出钟楼的高度,于是在地面上的C处放置了一面镜子,当他站在离镜子C处的E处时,恰好从镜子里看到钟楼顶端A在镜子中的像(即).已知B,C,E在同一直线上,小琪的眼睛离地面的高度 , , 求钟楼的高度. 21. 如图,在一个游戏活动节目中,需要设计一个可以自由转动的转盘,转盘被分成两个标有数字的扇形区域.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字.(若指针指向两个扇形的交线,则重新转动转盘,直到指针指向一个扇形的内部为止)
21. 如图,在一个游戏活动节目中,需要设计一个可以自由转动的转盘,转盘被分成两个标有数字的扇形区域.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字.(若指针指向两个扇形的交线,则重新转动转盘,直到指针指向一个扇形的内部为止)下表是进行试验时,转动转盘记录的一些数据:
转动转盘的次数(m)
150
200
400
600
落在“1”区域的次数(n)
52
67
133
200
落在“1”区域的频率()
 (1)、根据上表数据,估计标有数字“1”的扇形区域的圆心角度数为 . (该圆心角度数为的倍数)(2)、转动转盘两次,用画树状图或列表法求出这两次转出的数字之和等于3的概率.22. 某鞋店销售A,B两种型号的球鞋,销售一双A型球鞋可获利80元,销售一双B型球鞋可获利元.该鞋店计划一次购进两种型号的球鞋共双,将其销售完可获总利润为y元,设其中A型球鞋x双.(1)、求y与x的函数关系式.(2)、若本次购进B型球鞋的数量不超过A型球鞋的倍,问如何安排购进方案,可获得最大利润.23. 学校体育组老师为了解学生课外体育锻炼运动情况,从全校三年级随机抽取了20名学生,并统计了这20名学生每周课外运动锻炼的时间(单位:min):
(1)、根据上表数据,估计标有数字“1”的扇形区域的圆心角度数为 . (该圆心角度数为的倍数)(2)、转动转盘两次,用画树状图或列表法求出这两次转出的数字之和等于3的概率.22. 某鞋店销售A,B两种型号的球鞋,销售一双A型球鞋可获利80元,销售一双B型球鞋可获利元.该鞋店计划一次购进两种型号的球鞋共双,将其销售完可获总利润为y元,设其中A型球鞋x双.(1)、求y与x的函数关系式.(2)、若本次购进B型球鞋的数量不超过A型球鞋的倍,问如何安排购进方案,可获得最大利润.23. 学校体育组老师为了解学生课外体育锻炼运动情况,从全校三年级随机抽取了20名学生,并统计了这20名学生每周课外运动锻炼的时间(单位:min):60 81 50 44 110 130 146 80 100 30 80 120 140 75 81 10 30 81 92 60
(1)、体育组老师采取的调查方式是 . (填普查或抽样调查)(2)、这20名学生每周课外体育运动锻炼的时间的中位数是 , 众数是 .(3)、如果该校现有学生800人,估计该校学生每周课外体育运动锻炼的时间不少于80分钟的人数.24. 如图,是的直径,C在的延长线上,与相切于点D,过点A作 , 垂足为E.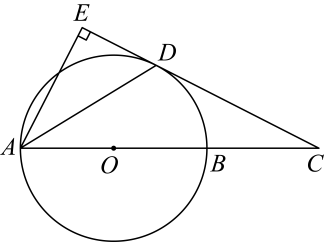 (1)、求证:平分 .(2)、若 , , 求的半径以及线段的长.25. 如图,抛物线L:与x轴交于 , B两点,与y轴交于点 , D为抛物线L的顶点.
(1)、求证:平分 .(2)、若 , , 求的半径以及线段的长.25. 如图,抛物线L:与x轴交于 , B两点,与y轴交于点 , D为抛物线L的顶点. (1)、求抛物线L的表达式.(2)、将抛物线L向右平移,平移后所得的抛物线与x轴交于点 , , 交y轴于点 , 顶点为 . 若 , 求抛物线的表达式.26. 问题研究
(1)、求抛物线L的表达式.(2)、将抛物线L向右平移,平移后所得的抛物线与x轴交于点 , , 交y轴于点 , 顶点为 . 若 , 求抛物线的表达式.26. 问题研究
如图1,是的中线,是边上的高.
(1)、当 , , 时, .(2)、求证: .(3)、某地为打造元宵节灯展景观,需按如下要求设计一批灯展造型.如图2,矩形是造型框架,以顶点A为圆心悬挂圆形灯架(),以B,C为顶点钉两个正方形展板(正方形和正方形),接合点点E恰好在上.若 , , 的半径为 , 求两个正方形展板面积和的最小值.