陕西省渭南市临渭区2023年中考一模数学试卷
试卷更新日期:2023-05-23 类型:中考模拟
一、单选题
-
1. 计算的结果是( )A、 B、 C、3 D、52. 如图, , , 连接 , 若 , 则的度数为 ( )
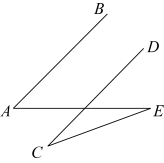 A、 B、 C、 D、3. 计算的结果为( )A、 B、 C、 D、4. 如图,在矩形中,对角线交于点O,下列条件中,能使矩形成为正方形的是( )
A、 B、 C、 D、3. 计算的结果为( )A、 B、 C、 D、4. 如图,在矩形中,对角线交于点O,下列条件中,能使矩形成为正方形的是( )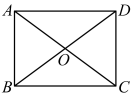 A、 B、 C、 D、5. 已知直线与相交于点则关于x的方程的解是( )A、x=-1 B、x=1 C、x=2 D、x=36. 如图,在中, , D是的中点,过D点作的垂线交于点E, , , 则的长为( )
A、 B、 C、 D、5. 已知直线与相交于点则关于x的方程的解是( )A、x=-1 B、x=1 C、x=2 D、x=36. 如图,在中, , D是的中点,过D点作的垂线交于点E, , , 则的长为( ) A、4 B、 C、 D、7. 如图,已知是的一条弦, , 点M在上,且 , 若 , 则⊙O的半径为( )
A、4 B、 C、 D、7. 如图,已知是的一条弦, , 点M在上,且 , 若 , 则⊙O的半径为( )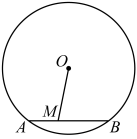 A、4 B、5 C、6 D、8. 已知抛物线(a,h是常数)与y轴的交点为A,点A与点B关于抛物线的对称轴对称,抛物线中的自变量x与函数值y的部分对应值如表:
A、4 B、5 C、6 D、8. 已知抛物线(a,h是常数)与y轴的交点为A,点A与点B关于抛物线的对称轴对称,抛物线中的自变量x与函数值y的部分对应值如表:x
…
0
1
3
4
…
…
6
…
下列结论正确的是( )
A、抛物线的对称轴是直线 B、当时,y随x的增大而增大 C、将抛物线向上平移1个单位后经过原点 D、点A的坐标是 , 点B的坐标是二、填空题
-
9. 因式分解: .10. 如图,数轴上的A、B两点所表示的数分别为a、b,则0.(填“>”“<”或“=”)
 11. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积.如图,若用圆的内接正八边形的面积来近似估计的面积S,设的半径为2,则的值为 . (结果保留和根号)
11. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积.如图,若用圆的内接正八边形的面积来近似估计的面积S,设的半径为2,则的值为 . (结果保留和根号) 12. 如图,点A是反比例函数图象上的一点,连接 , 点B是的中点,过点B作x轴的平行线,分别交y轴和反比例函数的图象于点C、D,连接 , 若的面积为3,则k的值为
12. 如图,点A是反比例函数图象上的一点,连接 , 点B是的中点,过点B作x轴的平行线,分别交y轴和反比例函数的图象于点C、D,连接 , 若的面积为3,则k的值为 13. 如图,在菱形中, , 点E为边的中点,点P在对角线上运动,且 , 则长的最大值为 .
13. 如图,在菱形中, , 点E为边的中点,点P在对角线上运动,且 , 则长的最大值为 .
三、解答题
-
14. 计算:15. 解不等式 >x﹣1,并写出它的所有正整数解.16. 解方程:17. 如图,在中, , , 在上求作一点D,使得 . (要求:尺规作图,不写作法,保留作图痕迹)
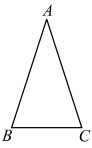 18. 如图,点B、F、C、E在同一条直线上, , , . 求证: .
18. 如图,点B、F、C、E在同一条直线上, , , . 求证: . 19. 如图,在边长为1的正方形网格中,ABC的顶点均在格点上,将ABC绕点A顺时针方向旋转90°后,得到 , 点B、C的对应点分别为 .
19. 如图,在边长为1的正方形网格中,ABC的顶点均在格点上,将ABC绕点A顺时针方向旋转90°后,得到 , 点B、C的对应点分别为 .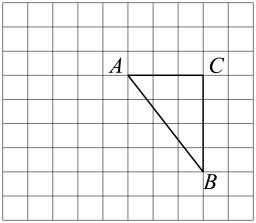 (1)、画出旋转后的;(2)、求点B绕点A旋转到所经过的路径长.(结果保留π)20. “四大发明”是指中国古代对世界具有很大影响的四种发明,它是中国古代劳动人民的重要创造,具体指印刷术、造纸术、火药和指南针四项发明.如图是小沈同学收集到的中国古代四大发明卡片,四张卡片除内容外其余完全相同,将这四张卡片背面朝上,洗匀放好.
(1)、画出旋转后的;(2)、求点B绕点A旋转到所经过的路径长.(结果保留π)20. “四大发明”是指中国古代对世界具有很大影响的四种发明,它是中国古代劳动人民的重要创造,具体指印刷术、造纸术、火药和指南针四项发明.如图是小沈同学收集到的中国古代四大发明卡片,四张卡片除内容外其余完全相同,将这四张卡片背面朝上,洗匀放好. (1)、从这四张卡片中随机抽取一张恰好是“指南针”的概率为;(2)、从这四张卡片中随机抽取一张(不放回),再从中随机抽取一张.请用列表或画树状图的方法,求抽到的两张卡片恰好是“印刷术”和“造纸术”的概率.21. 消防车是救援火灾的主要装备.图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂(20米米)是可伸缩的,且起重臂AC可绕点A在一定范围内上下转动,张角为(),转动点A距离地面的高度米.已知 , , 点B、E、F、D在同一水平线上,当起重臂的长为24米,张角时,求云梯消防车最高点C距离地面的高度 .
(1)、从这四张卡片中随机抽取一张恰好是“指南针”的概率为;(2)、从这四张卡片中随机抽取一张(不放回),再从中随机抽取一张.请用列表或画树状图的方法,求抽到的两张卡片恰好是“印刷术”和“造纸术”的概率.21. 消防车是救援火灾的主要装备.图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂(20米米)是可伸缩的,且起重臂AC可绕点A在一定范围内上下转动,张角为(),转动点A距离地面的高度米.已知 , , 点B、E、F、D在同一水平线上,当起重臂的长为24米,张角时,求云梯消防车最高点C距离地面的高度 .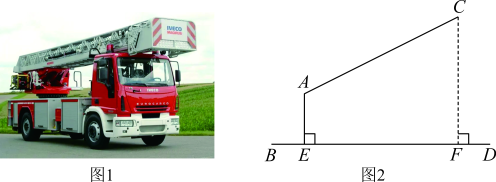 22. 习总书记说过“绿树青山就是金山银山”,为了保护林业资源,美化环境,保持生态平衡,世界上很多国家都根据本国实际情况设立了植树节,每年的3月12日是我国的义务植树节,植树节的意义是“绿化祖国,改善环境”.某校开展了“同享一片蓝天,共建美好家园”义务植树活动,为了解九年级同学义务植树的情况,进行抽样调查,随机抽取了30名九年级同学植树的棵数,收集的数据如下(单位:棵):
22. 习总书记说过“绿树青山就是金山银山”,为了保护林业资源,美化环境,保持生态平衡,世界上很多国家都根据本国实际情况设立了植树节,每年的3月12日是我国的义务植树节,植树节的意义是“绿化祖国,改善环境”.某校开展了“同享一片蓝天,共建美好家园”义务植树活动,为了解九年级同学义务植树的情况,进行抽样调查,随机抽取了30名九年级同学植树的棵数,收集的数据如下(单位:棵):1 1 2 4 2 3 2 3 3 4 3 3 4 3 3
5 3 4 3 4 4 5 4 5 3 4 3 4 5 6
对以上数据进行整理、描述和分析,并绘制出如图所示的条形统计图(不完整)
 (1)、请补全条形统计图;(2)、这30名九年级同学义务植树数量的中位数是棵,众数是棵;(3)、若该校九年级有600名同学参加义务植树活动,请你估计在本次义务植树活动中九年级同学植树的总棵数.23. 华山古称“西岳”,为五岳之一,中华的“华”源于华山,因此华山有了“华夏之根”之称,华山南接秦岭山脉,北瞰黄渭,自古以来就有“奇险天下第一山”的说法.甲、乙两人住同一小区,该小区到华山的距离为300千米,两人先后从家出发沿同一路线驾车驶向华山,如图,线段表示甲离开家的距离y(千米)与时间t(小时)之间的函数关系;线段表示乙离开家的距离y(千米)与时间t(小时)之间的函数关系.点C在线段上,请根据图象解答下列问题:
(1)、请补全条形统计图;(2)、这30名九年级同学义务植树数量的中位数是棵,众数是棵;(3)、若该校九年级有600名同学参加义务植树活动,请你估计在本次义务植树活动中九年级同学植树的总棵数.23. 华山古称“西岳”,为五岳之一,中华的“华”源于华山,因此华山有了“华夏之根”之称,华山南接秦岭山脉,北瞰黄渭,自古以来就有“奇险天下第一山”的说法.甲、乙两人住同一小区,该小区到华山的距离为300千米,两人先后从家出发沿同一路线驾车驶向华山,如图,线段表示甲离开家的距离y(千米)与时间t(小时)之间的函数关系;线段表示乙离开家的距离y(千米)与时间t(小时)之间的函数关系.点C在线段上,请根据图象解答下列问题: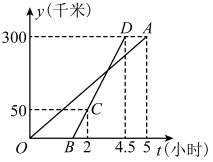 (1)、求点B的坐标;(2)、在整个过程中 , 求t为何值时,甲、乙两人之间的距离恰好为30千米.24. 如图,是的直径,点C、D在上,且点D是劣弧的中点,连接、、BD,与交于点E,过点A作的切线交的延长线于点F.
(1)、求点B的坐标;(2)、在整个过程中 , 求t为何值时,甲、乙两人之间的距离恰好为30千米.24. 如图,是的直径,点C、D在上,且点D是劣弧的中点,连接、、BD,与交于点E,过点A作的切线交的延长线于点F.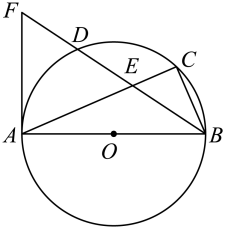 (1)、求证:;(2)、若 , , 求的长.25. 如图,在水平地面点A处有一网球发射器向空中发射网球,网球在地面上的落点为B,网球的飞行路线是一条抛物线,已知米,米.网球飞行的最大高度米.
(1)、求证:;(2)、若 , , 求的长.25. 如图,在水平地面点A处有一网球发射器向空中发射网球,网球在地面上的落点为B,网球的飞行路线是一条抛物线,已知米,米.网球飞行的最大高度米.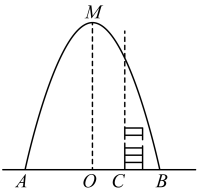 (1)、建立合适的平面直角坐标系,求抛物线的函数表达式.(2)、小明在直线上,点C右侧竖直向上摆放若干个无盖的直径为0.5米,高为0.3米的圆柱形桶(网球的体积和圆柱形桶的厚度忽略不计),若要是网球刚好落入桶内,至少摆放多少个圆柱形桶?26. 【结论理解】“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形的四个顶点共圆.该小组继续利用上述结论进行探究.
(1)、建立合适的平面直角坐标系,求抛物线的函数表达式.(2)、小明在直线上,点C右侧竖直向上摆放若干个无盖的直径为0.5米,高为0.3米的圆柱形桶(网球的体积和圆柱形桶的厚度忽略不计),若要是网球刚好落入桶内,至少摆放多少个圆柱形桶?26. 【结论理解】“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形的四个顶点共圆.该小组继续利用上述结论进行探究. (1)、【问题探究】如图1,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折,点C的对应点F恰好落在边AD上,做经过F、E、C三点的圆,请根据以上结论判断点B点(填“在”或“不在”)该圆上;(2)、如图2,四边形是的内接四边形, , , , 求四边形的面积.(3)、【问题解决】如图3,四边形是某公园的一块空地,现计划在空地中修建与两条小路,(小路宽度不计),将这块空地分成四部分,记两条小路的交点为P,其中与空地中种植草坪,与空地中分别种植郁金香和牡丹花.已知 , 且点C到的距离是 , 求种植牡丹花的地块的面积比种植郁金香的地块的面积多多少?
(1)、【问题探究】如图1,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折,点C的对应点F恰好落在边AD上,做经过F、E、C三点的圆,请根据以上结论判断点B点(填“在”或“不在”)该圆上;(2)、如图2,四边形是的内接四边形, , , , 求四边形的面积.(3)、【问题解决】如图3,四边形是某公园的一块空地,现计划在空地中修建与两条小路,(小路宽度不计),将这块空地分成四部分,记两条小路的交点为P,其中与空地中种植草坪,与空地中分别种植郁金香和牡丹花.已知 , 且点C到的距离是 , 求种植牡丹花的地块的面积比种植郁金香的地块的面积多多少?