鲁教版(五四制)2022-2023学年度第二学期七年级数学 三角形内角和定理 期末复习
试卷更新日期:2023-05-23 类型:复习试卷
一、单选题
-
1. 如图, , 点在 , 之间, , 连接 , 若 , , 下列说法中正确的是( )
 A、当时, B、当时, C、当时, D、不可能为2. 一副直角三角板如图放置,点C在FD的延长线上, , , , , 则为( )
A、当时, B、当时, C、当时, D、不可能为2. 一副直角三角板如图放置,点C在FD的延长线上, , , , , 则为( ) A、10° B、15° C、25° D、30°3. 要得知作业纸上两相交直线 , 所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案如图1和图2):
A、10° B、15° C、25° D、30°3. 要得知作业纸上两相交直线 , 所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案如图1和图2):
图 图
对于方案Ⅰ、Ⅱ,说法正确的是
 ( )A、Ⅰ可行、Ⅱ不可行 B、Ⅰ不可行、Ⅱ可行 C、Ⅰ、Ⅱ都可行 D、Ⅰ、Ⅱ都不可行4. 下列说法中,正确的个数为( )
( )A、Ⅰ可行、Ⅱ不可行 B、Ⅰ不可行、Ⅱ可行 C、Ⅰ、Ⅱ都可行 D、Ⅰ、Ⅱ都不可行4. 下列说法中,正确的个数为( )①三角形的高、中线、角平分线都是线段②三角形的外角大于任意一个内角③△ABC中,∠A=2∠B=3∠C,则△ABC是直角三角形④若a、b、c均大于0,且满足a+b>c,则长为a、b、c的三条线段一定能组成三角形
A、1 B、2 C、3 D、45. 如图,与交于点 , 点在直线上,交于点 , , , .下列说法中:①;②;③;④ , 其中正确的是( )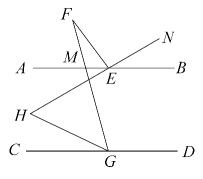 A、①② B、①④ C、①②④ D、②④6. 如图, , 于点C,的延长线与交于点E,若 , 则等于( )
A、①② B、①④ C、①②④ D、②④6. 如图, , 于点C,的延长线与交于点E,若 , 则等于( ) A、 B、 C、 D、7. 如图,已知 , 点E,F分别在直线上,点P在之间且在的左侧.若将射线沿折叠,射线沿折叠,折叠后的两条射线互相垂直,则的度数为( )
A、 B、 C、 D、7. 如图,已知 , 点E,F分别在直线上,点P在之间且在的左侧.若将射线沿折叠,射线沿折叠,折叠后的两条射线互相垂直,则的度数为( ) A、 B、 C、或 D、或或8. 如图,已知,∠BAC=∠ACD=90°,∠ABC=∠ADC,CE⊥AD.有下列结论:①AD∥BC;②∠ECD=∠DAC;③∠CEF=∠CFE;④CACE=∠ABC.其中正确的结论有( )
A、 B、 C、或 D、或或8. 如图,已知,∠BAC=∠ACD=90°,∠ABC=∠ADC,CE⊥AD.有下列结论:①AD∥BC;②∠ECD=∠DAC;③∠CEF=∠CFE;④CACE=∠ABC.其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个9. 如图,AB∥CD,点P在AB,CD之间,∠ACP=2∠PCD=40°,连结AP,若∠BAP=α,∠CAP=α+β.下列说法中正确的是( )
A、1个 B、2个 C、3个 D、4个9. 如图,AB∥CD,点P在AB,CD之间,∠ACP=2∠PCD=40°,连结AP,若∠BAP=α,∠CAP=α+β.下列说法中正确的是( )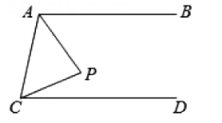 A、当∠P=60°时,α=30° B、当∠P=60°时,β=40° C、当=20°时,∠P=90° D、当β=0°时,∠P=90°10. 利用透镜我们可以聚合或分散光线,它被广泛应用于显微设备、射电天文、汽车雷达等领域,如图经过透镜后的光线互相平行,已知∠A=164°,∠C=171°,则∠AOC=( )
A、当∠P=60°时,α=30° B、当∠P=60°时,β=40° C、当=20°时,∠P=90° D、当β=0°时,∠P=90°10. 利用透镜我们可以聚合或分散光线,它被广泛应用于显微设备、射电天文、汽车雷达等领域,如图经过透镜后的光线互相平行,已知∠A=164°,∠C=171°,则∠AOC=( ) A、20° B、25° C、30° D、35°
A、20° B、25° C、30° D、35°二、填空题
-
11. 一副三角尺的摆放位置如图所示,则的度数是 .
 12. 如图, , , 点、分别是线段和上的动点,在两点运动到某一位置时,恰好使得 , 此时量得 , , , 则.
12. 如图, , , 点、分别是线段和上的动点,在两点运动到某一位置时,恰好使得 , 此时量得 , , , 则. 13. 如图,直线 , , , 则的度数是 度
13. 如图,直线 , , , 则的度数是 度 14. 如图,在四边形纸片中 , 将纸片折叠,点、分别落在、处,折痕为 , 与交于点.若 , 则的度数为.
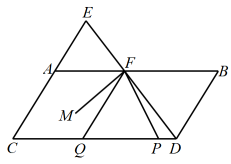
14. 如图,在四边形纸片中 , 将纸片折叠,点、分别落在、处,折痕为 , 与交于点.若 , 则的度数为. 15. 如图,点E在的延长线上,与交于点F,且 , , , P为线段上一动点,Q为上一点,且满足 , 为的平分线.下列结论:
15. 如图,点E在的延长线上,与交于点F,且 , , , P为线段上一动点,Q为上一点,且满足 , 为的平分线.下列结论:①;②平分;③;④.
其中结论正确的有(填写所有正确结论的序号).
三、解答题
-
16. 如图所示,已知直线EF和AB,CD分别相交于K,H,且EG⊥AB,∠CHF=600 , ∠E=30°,试说明AB∥CD.
 17. 如图,直线 , 平分 , , 垂足为点 , = , 求的度数.
17. 如图,直线 , 平分 , , 垂足为点 , = , 求的度数. 18. 如图,在中, , , AD是的角平分线,求的度数.
18. 如图,在中, , , AD是的角平分线,求的度数.
四、综合题
-
19. 如图,在中, , 点是线段上一点.
 (1)、尺规作图:在内作 , 与边交于点(保留作图痕迹,不用写作法);(2)、在(1)的条件下,当时,求的度数.20. 如图,已知AD∥BC,点E在AB的延长线上,连结DE交BC于点F,且∠C=∠A.
(1)、尺规作图:在内作 , 与边交于点(保留作图痕迹,不用写作法);(2)、在(1)的条件下,当时,求的度数.20. 如图,已知AD∥BC,点E在AB的延长线上,连结DE交BC于点F,且∠C=∠A. (1)、请说明∠E=∠CDE的理由;(2)、若∠1=75°,∠E=30°,求∠A的度数.21. 已知:点A在射线上,.
(1)、请说明∠E=∠CDE的理由;(2)、若∠1=75°,∠E=30°,求∠A的度数.21. 已知:点A在射线上,. (1)、如图 , 若 , 说明的理由;(2)、如图2,若 , 与交于点 , 请探究与的数量关系,写出你的探究结论,并说明理由.22. 如图,在△ABC中,∠A=∠ABC,直线EF分别交AB、AC和CB的延长线于点D、E、F,过点B作BP//AC交EF于点P.
(1)、如图 , 若 , 说明的理由;(2)、如图2,若 , 与交于点 , 请探究与的数量关系,写出你的探究结论,并说明理由.22. 如图,在△ABC中,∠A=∠ABC,直线EF分别交AB、AC和CB的延长线于点D、E、F,过点B作BP//AC交EF于点P. (1)、若∠A=70°,∠F=25°,求∠BPD的度数.(2)、求证:∠F+∠FEC=2∠ABP.23. 如图1,将一只含角的直角三角板按如图摆放,其中 , 顶点A,C分别在直线上(),此时恰好平分 , 交直线于D点,过D点作交于E点,连接 , 在上取一点F,使 , 的角平分线交于G点.
(1)、若∠A=70°,∠F=25°,求∠BPD的度数.(2)、求证:∠F+∠FEC=2∠ABP.23. 如图1,将一只含角的直角三角板按如图摆放,其中 , 顶点A,C分别在直线上(),此时恰好平分 , 交直线于D点,过D点作交于E点,连接 , 在上取一点F,使 , 的角平分线交于G点.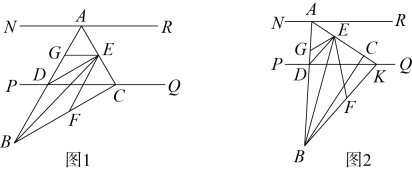 (1)、°;(2)、求证:平分;(3)、现将三角板绕顶点A逆时针旋转一定的度数(如图2),的延长线交于点K,连接 , 过D点作交于E点,在上取一点F,使得相等,的角平分线交于G点,若 , 求此时的度数.
(1)、°;(2)、求证:平分;(3)、现将三角板绕顶点A逆时针旋转一定的度数(如图2),的延长线交于点K,连接 , 过D点作交于E点,在上取一点F,使得相等,的角平分线交于G点,若 , 求此时的度数.