鲁教版(五四制)2022-2023学年度第二学期七年级数学 平行线的性质定理 期末复习
试卷更新日期:2023-05-23 类型:复习试卷
一、单选题
-
1. 如图, , 交于点 , 平分 , , 则的度数为( )
 A、 B、 C、 D、2. 如图, , 点在 , 之间, , 连接 , 若 , , 下列说法中正确的是( )
A、 B、 C、 D、2. 如图, , 点在 , 之间, , 连接 , 若 , , 下列说法中正确的是( ) A、当时, B、当时, C、当时, D、不可能为3. 一副直角三角板如图放置,点C在FD的延长线上, , , , , 则为( )
A、当时, B、当时, C、当时, D、不可能为3. 一副直角三角板如图放置,点C在FD的延长线上, , , , , 则为( ) A、10° B、15° C、25° D、30°4. 如图,直线a∥b,∠1=80°,那么∠2的度数是( )
A、10° B、15° C、25° D、30°4. 如图,直线a∥b,∠1=80°,那么∠2的度数是( ) A、120° B、100° C、80° D、70°5. 如图, , , , , 给出以下结论: ; ; ; . 其中正确的结论有( )
A、120° B、100° C、80° D、70°5. 如图, , , , , 给出以下结论: ; ; ; . 其中正确的结论有( )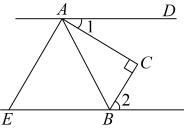 A、1个 B、2个 C、3个 D、4个6. 如图,若 , 那么( ).
A、1个 B、2个 C、3个 D、4个6. 如图,若 , 那么( ). A、 B、 C、 D、7. 如图, , , 则α、β、γ的关系是( )
A、 B、 C、 D、7. 如图, , , 则α、β、γ的关系是( )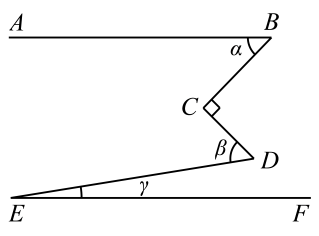 A、 B、 C、 D、8. 如图所示,AB∥CD∥EF,则下列等式中正确的是( ).
A、 B、 C、 D、8. 如图所示,AB∥CD∥EF,则下列等式中正确的是( ). A、∠1=180°-∠3 B、∠1=∠3-∠2. C、∠2+∠3=180°-∠1 D、∠2+∠3=180°+∠19. 如图, , 点P在射线上.分别平分 , , 若 , 且 , 则的度数为( )
A、∠1=180°-∠3 B、∠1=∠3-∠2. C、∠2+∠3=180°-∠1 D、∠2+∠3=180°+∠19. 如图, , 点P在射线上.分别平分 , , 若 , 且 , 则的度数为( ) A、 B、 C、 D、10. 如图,生活中,将一个宽度相等的纸条按右图所示折叠一下,如果∠1=140°,那么∠2的度数为( )
A、 B、 C、 D、10. 如图,生活中,将一个宽度相等的纸条按右图所示折叠一下,如果∠1=140°,那么∠2的度数为( ) A、140° B、120° C、110° D、100°
A、140° B、120° C、110° D、100°二、填空题
-
11. 有一条直的宽纸带,按如图所示的方式折叠,的度数为 .
 12. 如图,已知AB∥CD,∠B=110°,EF平分∠BEC,EG⊥EF,则∠DEG= .
12. 如图,已知AB∥CD,∠B=110°,EF平分∠BEC,EG⊥EF,则∠DEG= .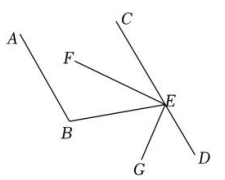 13. 如图是某灯具的镜面反射示意图,从光源点处发出的光线 , 经弯曲的镜面反射后射出,且满足反射光线 , 若 , 于点 , 则的度数为 .
13. 如图是某灯具的镜面反射示意图,从光源点处发出的光线 , 经弯曲的镜面反射后射出,且满足反射光线 , 若 , 于点 , 则的度数为 .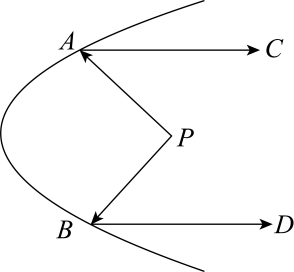 14. 如图,已知 , 、分别在、上,点在、之间,连接、 , , 平分 , 平分 , 在的下方有一点 , 平分 , 平分 , 求的度数为 .
14. 如图,已知 , 、分别在、上,点在、之间,连接、 , , 平分 , 平分 , 在的下方有一点 , 平分 , 平分 , 求的度数为 .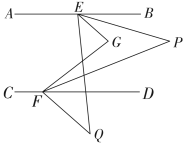 15. 如图,已知长方形纸片 , 点和点分别在边和上,且 , 点和点分别是边和上的动点,现将点 , , , 分别沿 , 折叠至点 , , , , 若 , 则的度数为 .
15. 如图,已知长方形纸片 , 点和点分别在边和上,且 , 点和点分别是边和上的动点,现将点 , , , 分别沿 , 折叠至点 , , , , 若 , 则的度数为 .
三、解答题
-
16. 如图:已知 , 若 , 求的度数.
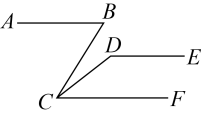 17. 如图, , 直线分别交、于点E,F,平分 , . 求和的度数.
17. 如图, , 直线分别交、于点E,F,平分 , . 求和的度数.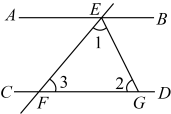 18. 如图,已知 , , 求 .
18. 如图,已知 , , 求 .
四、综合题
-
19. 如图,已知∠BGE=∠CHF,射线HM平分∠EHC交AB于点N
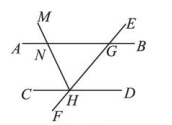 (1)、证明:AB//CD;(2)、若∠BGE=40°,求∠BNM的度数.20. 已知 , 分别与交于 , 点是上的定点,点是直线上一动点(点不与点重合),
(1)、证明:AB//CD;(2)、若∠BGE=40°,求∠BNM的度数.20. 已知 , 分别与交于 , 点是上的定点,点是直线上一动点(点不与点重合),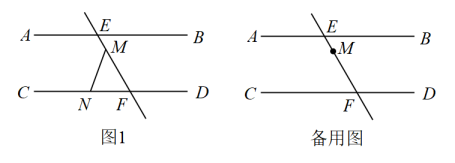 (1)、如图1,若 , , 求的度数.(2)、点在运动的过程中,探究 , 和的数量关系,并说明理由.21. 如图,在中, , 点是线段上一点.
(1)、如图1,若 , , 求的度数.(2)、点在运动的过程中,探究 , 和的数量关系,并说明理由.21. 如图,在中, , 点是线段上一点. (1)、尺规作图:在内作 , 与边交于点(保留作图痕迹,不用写作法);(2)、在(1)的条件下,当时,求的度数.22. 如图,将一个长方形纸片沿所在直线折叠,使得点C,D的对应点分别为点N,M,NF交于点G,过点G作 , 交于点H.
(1)、尺规作图:在内作 , 与边交于点(保留作图痕迹,不用写作法);(2)、在(1)的条件下,当时,求的度数.22. 如图,将一个长方形纸片沿所在直线折叠,使得点C,D的对应点分别为点N,M,NF交于点G,过点G作 , 交于点H. (1)、若 , 求的度数;(2)、求证:平分.23. [阅读探究]如图(a)所示,已知AB∥CD,点E,F分别是AB,CD上的点,点M在AB,CD两平行线之间,∠AEM=45°,∠CFM=25°,求∠EMF的度数.
(1)、若 , 求的度数;(2)、求证:平分.23. [阅读探究]如图(a)所示,已知AB∥CD,点E,F分别是AB,CD上的点,点M在AB,CD两平行线之间,∠AEM=45°,∠CFM=25°,求∠EMF的度数.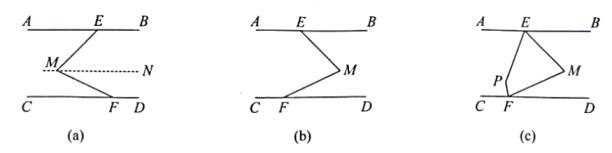
解:如图(a)所示,过点M作MN∥AB.
∵AB∥CD,
∴MN∥CD.
∴∠EMN= CAEM=45°,∠FMN=∠CFM= 25°.
∴∠EMF=∠EMN+∠FMN=45°+25°=70°.
(1)、从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠AEM和∠CFM“凑”在一起,得出角之间的关系,使问题得以解决.通过进一步研究,我们可以发现图(a)中∠AEM,∠EMF和∠CFM之间存在一定的数量关系,请直接写出它们之间的数量关系:(2)、[方法运用]如图(b)所示,已知AB∥CD,点E,F分别在直线AB,CD上,点M在AB,CD之间,求∠AEM,∠EMF和∠CFM之间的数量关系.(3)、[应用拓展]如图(C)所示,在图(b)的条件下,分别作LAEM和∠CFM的角平分线EP,FP,交于点P (交点P在AB,CD之间).若∠EMF=60°,求∠EPF的度数. .