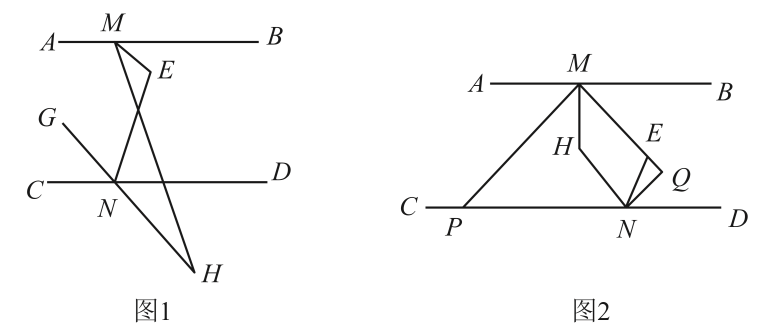鲁教版(五四制)2022-2023学年度第二学期七年级数学 平行线的判定定理 期末复习
试卷更新日期:2023-05-23 类型:复习试卷
一、单选题
-
1. 如图,下列条件中不能判定的是( )
 A、 B、 C、 D、2. 如图,在下列给出的条件中,不能判定的是( )
A、 B、 C、 D、2. 如图,在下列给出的条件中,不能判定的是( ) A、 B、 C、 D、3. 如图,下列条件中,不能判定AB∥CD的是( )
A、 B、 C、 D、3. 如图,下列条件中,不能判定AB∥CD的是( ) A、∠D+∠BAD=180° B、∠1=∠2 C、∠B=∠DCE D、∠3=∠44. 在数学课上,老师画一条直线a,按如图所示的方法,画一条直线b与直线a平行,再向上推三角尺,画一条直线c也与直线a平行,此时,发现直线b与直线c也平行,这就说明了( )
A、∠D+∠BAD=180° B、∠1=∠2 C、∠B=∠DCE D、∠3=∠44. 在数学课上,老师画一条直线a,按如图所示的方法,画一条直线b与直线a平行,再向上推三角尺,画一条直线c也与直线a平行,此时,发现直线b与直线c也平行,这就说明了( ) A、如果两条直线都和第三条直线平行,那么这两条直线也互相平行 B、两直线平行,同位角相等 C、同旁内角相等,两直线平行 D、过直线外一点,有且只有一条直线与已知直线5. 如图,下列说法错误的是( )
A、如果两条直线都和第三条直线平行,那么这两条直线也互相平行 B、两直线平行,同位角相等 C、同旁内角相等,两直线平行 D、过直线外一点,有且只有一条直线与已知直线5. 如图,下列说法错误的是( ) A、因为 , 所以 B、因为 , 所以 C、因为 , 所以 D、因为 , 所以6. 如图,与交于点 , 点在直线上,交于点 , , , .下列说法中:①;②;③;④ , 其中正确的是( )
A、因为 , 所以 B、因为 , 所以 C、因为 , 所以 D、因为 , 所以6. 如图,与交于点 , 点在直线上,交于点 , , , .下列说法中:①;②;③;④ , 其中正确的是( )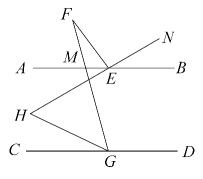 A、①② B、①④ C、①②④ D、②④7. 如图,由下列条件能判定的是( )
A、①② B、①④ C、①②④ D、②④7. 如图,由下列条件能判定的是( ) A、 B、 C、 D、8. 如图下列不能判定的条件是( )
A、 B、 C、 D、8. 如图下列不能判定的条件是( ) A、 B、 C、 D、9. 如图,已知∥ , , 分别平分和 , 且交于点 , 则( )
A、 B、 C、 D、9. 如图,已知∥ , , 分别平分和 , 且交于点 , 则( ) A、 B、 C、 D、10. 如图,下面推理过程正确的是( )
A、 B、 C、 D、10. 如图,下面推理过程正确的是( ) A、因为∠B=∠BCD,所以AB∥CD B、因为∠1=∠2.所以AB∥CD C、因为∠BAD+∠B=180°,所以AD∥BC D、因为∠1=∠B,所以AD∥BC
A、因为∠B=∠BCD,所以AB∥CD B、因为∠1=∠2.所以AB∥CD C、因为∠BAD+∠B=180°,所以AD∥BC D、因为∠1=∠B,所以AD∥BC二、填空题
-
11. 如图,已知长方形纸片 , 点和点分别在边和上,且 , 点和点分别是边和上的动点,现将点 , , , 分别沿 , 折叠至点 , , , , 若 , 则的度数为 .
 12. 如图,直线、被直线所截,若要使则需满足的一个条件是 .
12. 如图,直线、被直线所截,若要使则需满足的一个条件是 . 13. 如图所示绑在一起的木条.若测得 , , 要使木条 , 木条至少要旋转.
13. 如图所示绑在一起的木条.若测得 , , 要使木条 , 木条至少要旋转. 14. 如图,已知AB//CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°,∠BCD=40°,则∠BED的度数为.
14. 如图,已知AB//CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°,∠BCD=40°,则∠BED的度数为. 15. 如图,直线l1l2 , 若∠1=35°,则∠2+∠3=.
15. 如图,直线l1l2 , 若∠1=35°,则∠2+∠3=.
三、解答题
-
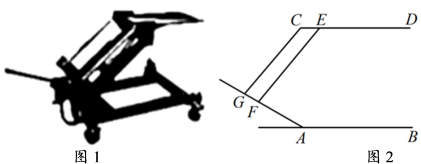
16. 如图1是一个由齿轮、轴承、托架等元件构成的手动变速箱托架,其主要作用是动力传输.如图2是手动变速箱托架工作时某一时刻的示意图,已知AB∥CD,CG∥EF,∠BAG=150°,∠AGC=80°,求∠DEF的度数.
 17. 如图, , , 求的度数.
17. 如图, , , 求的度数. 18. 如图所示,已知直线EF和AB,CD分别相交于K,H,且EG⊥AB,∠CHF=600 , ∠E=30°,试说明AB∥CD.
18. 如图所示,已知直线EF和AB,CD分别相交于K,H,且EG⊥AB,∠CHF=600 , ∠E=30°,试说明AB∥CD.
四、综合题
-
19. 在中, , 点D是BC上一点,将沿AD翻折后得到 , 边AE交射线BC于点F.
 (1)、如(图1),当时,求证:(2)、若 ,
(1)、如(图1),当时,求证:(2)、若 ,①如(图2),当时,求x的值.
②是否存在这样的x的值,使得中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
20. 一个长方形台球桌面如图1所示,已知台球在与台球桌边缘碰撞的过程中,撞击线路与桌边的夹角等于反弹线路与桌边的夹角,即图1中的. (1)、台球经过如图2所示的两次碰撞后,第二次的反弹线路为.若开始时的撞击线路为 , 求证:;(2)、台球桌因为长期使用,导致桌角松动变形如图3,在台球经过两次撞击之后,开始时的撞击线路EF所在直线与第二次的反弹线路所在直线相交于点M,若 , 求的度数.21. 如图,已知直线.
(1)、台球经过如图2所示的两次碰撞后,第二次的反弹线路为.若开始时的撞击线路为 , 求证:;(2)、台球桌因为长期使用,导致桌角松动变形如图3,在台球经过两次撞击之后,开始时的撞击线路EF所在直线与第二次的反弹线路所在直线相交于点M,若 , 求的度数.21. 如图,已知直线. (1)、在图1中,点E在直线上,点F在直线上,点G在之间,若 , , 则;(2)、如图2,若平分 , 延长交于点M,且 , 当时,求的度数;(3)、在(2)的条件下,若绕E点以每秒转动4°的速度逆时针旋转一周,同时绕F点以每秒转动1°的速度逆时针旋转,当转动结束时也随即停止转动,在整个转动过程中,当秒时,.
(1)、在图1中,点E在直线上,点F在直线上,点G在之间,若 , , 则;(2)、如图2,若平分 , 延长交于点M,且 , 当时,求的度数;(3)、在(2)的条件下,若绕E点以每秒转动4°的速度逆时针旋转一周,同时绕F点以每秒转动1°的速度逆时针旋转,当转动结束时也随即停止转动,在整个转动过程中,当秒时,.