鲁教版（五四制）2022-2023学年度第二学期七年级数学证明的必要性期末复习

试卷更新日期：2023-05-23 类型：复习试卷

进入出卷网下载

一、单选题

1. 试说明“若 $∠ A + ∠ B = 180 °$ ， $∠ C + ∠ D = 180 °$ ， $∠ A = ∠ C$ ，则 $∠ B = ∠ D$ ”是真命题．以下是排乱的推理过程：
①因为 $∠ A = ∠ C$ （已知）；
②因为 $∠ A + ∠ B = 180 °$ ， $∠ C + ∠ D = 180 °$ （已知）；
③所以 $∠ B = 180 ° - ∠ A$ ， $∠ D = 180 ° - ∠ C$ （等式的性质）；
④所以 $∠ B = ∠ D$ （等量代换）；
⑤所以 $∠ B = 180 ° - ∠ C$ （等量代换）．
正确的顺序是（）

A、①→③→②→⑤→④ B、②→③→⑤→①→④ C、②→③→①→⑤→④ D、②→⑤→①→③→④

查看试题解析
2. 网课期间，琪琪同学花整数元购买了一个手机支架，让同学们猜价格．甲说：“至少20元”，乙说“至多18元”，丙说：“至多15元”．琪琪说：“你们都猜错了．”则这个支架的价格为（）

A、15元 B、18元 C、19元 D、20元

查看试题解析
3. 将一副直角三角尺如图放置，已知∠EAD=∠E=45°，∠C=30°，AE∥BC，求∠AFD的度数，以下是打乱的推理过程：①∵∠E=45°，②∴∠AFD=∠E＋∠EAC=45°＋30°=75°；③∵∠C=30°，AE∥BC，④∴∠EAC=∠C=30°．推理步骤正确的是（）

A、①②③④ B、①④③② C、③④①② D、③②①④

查看试题解析
4. 甲、乙、丙3人从图书馆各借了一本书（如下表所示），他们相约在每个星期天相互交换读完的书，经过数次交换后，他们都读完了这3本书．已知甲读的第三本书是乙读的第二本书，则丙读的第二本书是（）
甲
乙
丙
书A
书B
书C

A、书A B、书B C、书C D、无法确定

查看试题解析
5. 在一次数学活动课上，王老师将1～8共八个整数依次写在八张不透明的卡片上（每张卡片上只写一个数字，每一个数字只写在一张卡片上，而且把写有数字的那一面朝下）．他先像洗扑克牌一样打乱这些卡片的顺序，然后把甲、乙、丙、丁四位同学叫到讲台上，随机地发给每位同学两张卡片，并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上，写出的结果依次是：甲：12；乙：11；丙：9；丁：4，则拿到数字5的同学是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 李明、王华、周亮和张红四名同学参加了“华罗庚杯”竞赛选拔赛，王华和张红两个同学的得分和等于周亮和李明的得分和；李明与王华的得分和大于周亮和张红的得分和，张红的得分超过周亮与王华的得分和，则这四位同学的得分由大到小的顺序是（）

A、李明，张红，周亮，王华 B、李明，张红，王华，周亮 C、张红，李明，周亮，王华 D、张红，李明，王华，周亮

查看试题解析
7. 嘉淇在证明“平行于同一条直线的两条直线平行”时，给出了如下推理过程：
已知：如图，b∥a，c∥a，求证：b∥c；
证明：作直线DF交直线a、b、c分
别于点D、E、F，
∵a∥b，∴∠1＝∠4，又∵a∥c，
∴∠1＝∠5，
∴b∥c．
小明为保证嘉淇的推理更严谨，想在方框中“∴∠1＝∠5”和“∴b∥c”之间作补充，下列说法正确的是（）

A、嘉淇的推理严谨，不需要补充 B、应补充∠2＝∠5 C、应补充∠3+∠5＝180° D、应补充∠4＝∠5

查看试题解析
8. 小英､小亮､小明和小华四名同学参加了“大梦杯”竞赛选拔赛，小亮和小华两个同学的得分和等于小明和小英的得分和；小英与小亮的得分和大于小明和小华的得分和；小华的得分超过小明与小亮的得分和.则这四位同学的得分由小到大的顺序是（）

A、小明、小亮、小华、小英 B、小明、小亮、小英、小华 C、小英、小华、小亮、小明 D、小亮、小英、小华、小明

查看试题解析
9. 有四位同学一起研究一道数学题．如图，已知EF⊥AB ， CD⊥AB ．则下列说法正确的是（）
甲说：“如果还知道∠CDG＝∠BFE ，则能得到∠AGD＝∠ACB ． ”

乙说：“把甲的已知和结论倒过来，即由∠AGD＝∠ACB ，可得到∠CDG＝∠BFE ． ”

丙说：“∠AGD一定大于∠BFE ． ”

丁说：“如果连接GF ，则GF一定平行于AB ． ”

A、甲对乙错 B、乙错丁对 C、甲、乙对 D、乙、丙对

查看试题解析
10. 已知四个实数a，b，c，d，若a>b，c>d，则（）

A、a+c>b+d B、a-c>b-d C、ac>bd D、 $\frac{a}{c} > \frac{b}{d}$

查看试题解析

二、填空题

11. 金乡县某中学七年级共有四个班，每班各选5名同学组成一个代表队，这四支代表队（分别用A，B，C，D表示）进行数学知识应用竞赛，前三名将参加金乡县数学知识竞赛，甲，乙，丙三位同学预测的结果分别为：甲：C得亚军；D得季军；乙：D得冠军；A得亚军；丙：C得冠军；B得亚军．已知每人的预测都是半句正确，半句错误，则冠，亚，季，殿军分别为．

查看试题解析
12. 为鼓励学生居家锻炼，李老师组织线上仰卧起坐接力活动.4人为一组，每人自主设定个人目标（单位：次），组内任意2人之间均需接力一场，且每场接力2人都达到个人目标即停止，记录每场接力成绩（2人所做仰卧起坐次数之和）．小贾、小易、小冰、小丁为一组，他们六场接力成绩由小到大依次为86，92，94，98，100，106．若他们设定的个人目标分别记为a，b，c，d，其中 $b < a < c < d$ ，且 $b + d < a + c$ ．根据以上信息，得到三个结论：① $a + b = 86$ ， $c + d = 100$ ；②六场接力成绩由小到大可以依次表示为： $a + b$ ， $b + c$ ， $b + d$ ， $a + c$ ， $a + d$ ， $c + d$ ；③a，b，c，d的值分别为46，40，52，54．其中正确结论的序号是．

查看试题解析
13. 小丽在4张同样的纸片上各写了一个正整数，从中随机抽取2张，并将它们上面的数相加．重复这样做，每次所得的和都是5，6，7，8中的一个数，并且这4个数都能取到．猜猜看，小丽在4张纸片上各写下的数是．

查看试题解析
14. 如图，长方形是由若干个小长方形和小正方形组成，从面积的角度研究这个图形，可以得到一个数学等式，这个数学等式是．（用图中的字母表示出来）

查看试题解析
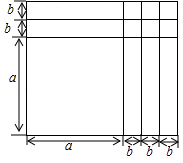15. 新定义：对非负数x“四舍五入”到个位的值记为（x）．即当n为非负整数时，若n﹣ $\frac{1}{2}$ ≤ x< n+ $\frac{1}{2}$ 则（x）＝n．如（0.46）＝0，（3.67）＝4．给出下列关于（x）的结论：
①（1.493）＝1；

②（2x）＝2（x）；

③若（ $\frac{1}{2}$ x-1）= 4，则x的取值范围是9≤x＜11；

④当x≥0，m为非负整数时，有（m+2020x）＝m+（2020x）；

其中正确的结论有（填写所有正确的序号）．

查看试题解析

三、解答题

16. 把下面的说理过程补充完整：
已知：如图，在四边形 $A B C D$ 中， $A B ∥ C D$ ，直线 $E F$ 与 $A D$ 和 $C B$ 的延长线分别交于点 $E$ ， $F$ ，若 $∠ D E F + ∠ E F C = 180 °$ ，那么 $∠ A$ 与 $∠ C$ 相等吗？请说明理由．
解： $∠ A = ∠ C$ ．理由如下：
因为 $∠ D E F + ∠ E F C = 180 °$ （已知），
所以  ▲   $∥$   ▲  （   ），
所以 $∠ A =$   ▲  （   ），
因为 $A B ∥$   ▲  （已知），
所以  ▲   $= ∠ C$ （  ），
所以 $∠ A = ∠ C$ （等量代换）．

查看试题解析
17. 补全解题过程．
已知：如图， $B D ⊥ A C$ 于点 $D$ ， $E F ⊥ A C$ 于点 $F$ ， $∠ 1 = ∠ 2$ ．
求证： $G D ∥ B C$ ．
证明：∵ $B D ⊥ A C$ ， $E F ⊥ A C$ ，
∴ $∠ B D C = ∠ E F C =$   ▲   $°$ ．
∴ $B D ∥ E F$ （   ）（填推理依据）．
∴ $∠ 2 = ∠$   ▲  （   ）（填推理依据）．
又∵ $∠ 1 = ∠ 2$ ，
∴ $∠ 1 = ∠$   ▲   ．
∴ $G D ∥ B C$ （   ）（填推理依据）．

查看试题解析
18. 如图，已知 $E F ∥ A D$ ， $∠ 1 = ∠ 2$ ， $∠ B A C = 70 °$ ，求 $∠ A G D$ （请填空）
解：∵ $E F ∥ A D$ （已知）
∴ $∠ 2 =$                   ▲                  （     ）
又∵ $∠ 1 = ∠ 2$ （已知）
∴ $∠ 1 =$                   ▲                  （    ）
∴                  ▲                   $∥$                   ▲                  （     ）
∴ $∠ B A C +$ $= 180 °$ （     ）
∵ $∠ B A C = 70 °$ （已知）
∴ $∠ A G D =$                   ▲

查看试题解析

四、综合题

19. 如图，已知 $A B = C D$ ， AB $∥$ CD， $E$ 、 $F$ 是 $A C$ 上两点，且 $A F = C E$ ．

(1)、证明： $A B E$ ≌ $△ C D F$ ．
证明： $∵ A F = C E$ （已知），
$∴ A F - E F = C E - E F$ （      ）
即 $A E = C F$ ．
∵ $A B ∥ C D$ ，
$∴ ∠ B A C = ∠ D C A$ （      ）
在 $△ A B E$ 和 $△ C D F$ 中，
$A B = C D$ ，
（      ），
$A E = C F$ ，
$∴ A B E$ ≌ $△ C D F$ （      ）

(2)、已知 $∠ A E B = 120 °$ ，求 $∠ D F E$ 的度数．

查看试题解析
20. 如图， $A B / / C D$ ， $A B = C D$ ，点 $E$ 、 $F$ 在 $B C$ 上，且 $B F = C E$ ．

(1)、填空：把下面的推理过程补充完整，并在括号内注明理由．
试说明： $Δ A B E ≌ Δ D C F$ ．

解： $∵ A B / / C D$ ，

$∴ ∠$      ▲    $= ∠$   ▲   （       ）．

$∵ B F = C E$ ，

即 $B E + E F = C F + E F$ ．

$∴$     ▲    $=$     ▲   （         ）．

又 $∵ A B = C D$ ，

$∴ Δ A B E ≅ Δ D C F$ （        ）．

(2)、由（1）可得， $A E$ 与 $D F$ 平行吗？请说明理由，

查看试题解析
21. 补全下面的证明过程和理由：
如图， $A B$ 和 $C D$ 相交于点O， $E F // A B$ ， $∠ C = ∠ C O A$ ， $∠ D = ∠ B O D$ ．

求证： $∠ A = ∠ F$

证明： $∵ ∠ C = ∠ C O A$ ， $∠ D = ∠ B O D$ ，

又 $∵ ∠ C O A = ∠ B O D$ （），

$∴ ∠ C =$ （）．

$∴ A C // D F$ （）．

$∴ ∠ A =$ （）．

$∵ E F // A B$ ，

$∴ ∠ F =$ （）．

$∴ ∠ A = ∠ F$ ．

查看试题解析
22. 完成以下推理过程：
如图，已知 $∠ A = ∠ 1$ ， $∠ C = ∠ F$ ，求证： $∠ C B A = ∠ E$ ．

证明： $∵ ∠ A = ∠ 1$ （已知）

$∴ A C / /$ ()

$∴ ∠ C =$ ()

又 $∵ ∠ C = ∠ F$ （已知）

$∴ ∠ F = ∠$ （等量代换）

$∴ B C / /$ ()

$∴ ∠ C B A = ∠ E ($ )

查看试题解析
23.
如图，已知AD∥CB，∠1＝∠2，∠BAE＝∠DCF。试说明：

(1)、AE∥CF；

(2)、AB∥CD。

查看试题解析

甲	乙	丙
书A	书B	书C

鲁教版（五四制）2022-2023学年度第二学期七年级数学 证明的必要性 期末复习

一、单选题

二、填空题

三、解答题

四、综合题

鲁教版（五四制）2022-2023学年度第二学期七年级数学证明的必要性期末复习