初中数学同步训练必刷题(人教版八年级下册 第十九章 一次函数)全章测试卷
试卷更新日期:2023-05-22 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 函数的自变量x的取值范围是( )A、x≠0 B、x≥且x≠0 C、x> D、x≥2. 直线是由( )单位长度得到的.A、向右平移8个 B、向左平移8个 C、向下平移8个 D、向上平移8个3. 根据图象,可得关于x的不等式k1x<k2x+b的解集是( )
 A、x<2 B、x>2 C、x<3 D、x>34. 设b>a,将一次函数y1=ax+b与y2=bx+a的图象画在同一平面直角坐标系中,则有组a,b的取值,使得下列四个备选答案中有一个是正确的,则这个正确的答案是( )A、
A、x<2 B、x>2 C、x<3 D、x>34. 设b>a,将一次函数y1=ax+b与y2=bx+a的图象画在同一平面直角坐标系中,则有组a,b的取值,使得下列四个备选答案中有一个是正确的,则这个正确的答案是( )A、 B、
B、 C、
C、 D、
D、 5. 一次函数y=5x-10的图象与正比例函数y=x的图象的交点是( )A、 B、 C、 D、(1,1)6. 在如图所示的计算程序中,y与x之间的函数关系式所对应的图象是( )
5. 一次函数y=5x-10的图象与正比例函数y=x的图象的交点是( )A、 B、 C、 D、(1,1)6. 在如图所示的计算程序中,y与x之间的函数关系式所对应的图象是( ) A、
A、 B、
B、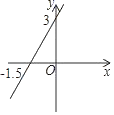 C、
C、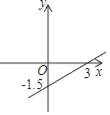 D、
D、 7. 关于一次函数的表述正确的是( )A、若函数图象经过第一、二、四象限,的值可能是3 B、无论为何值,图像一定经过 C、图象与轴的交点坐标 D、若两点 , 在该函数图象上,且 , 则8. 已知直线与交点的坐标为 , 则方程组的解是( )A、 B、 C、 D、9. 设 , 关于x的一次函数 , 当时,y的最小值是( )A、 B、 C、k D、10. “漏壶”是一种古代计时器,如图所示,在壶内盛一定量的水,水从壶底的小孔漏出,壶内壁画有刻度,人们根据壶中水面的位置计算时间.用x表示漏水时间,y表示壶底到水面的高度,不考虑水量变化对压力的影响,下列图象能表示y与x对应关系的是( )
7. 关于一次函数的表述正确的是( )A、若函数图象经过第一、二、四象限,的值可能是3 B、无论为何值,图像一定经过 C、图象与轴的交点坐标 D、若两点 , 在该函数图象上,且 , 则8. 已知直线与交点的坐标为 , 则方程组的解是( )A、 B、 C、 D、9. 设 , 关于x的一次函数 , 当时,y的最小值是( )A、 B、 C、k D、10. “漏壶”是一种古代计时器,如图所示,在壶内盛一定量的水,水从壶底的小孔漏出,壶内壁画有刻度,人们根据壶中水面的位置计算时间.用x表示漏水时间,y表示壶底到水面的高度,不考虑水量变化对压力的影响,下列图象能表示y与x对应关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(每空3分, 懂30分)
-
11. 函数的自变量的取值范围是 .12. 已知一次函数 , 当m时,y随x的增大而增大.13. 正比例函数y=kx的图象经过点(﹣2,6),则k= .14. 一次函数y=﹣2x+6的图象与x轴的交点坐标是 .15. 如图,已知直线和直线的交点坐标是(m,n),则关于x的不等式的解集是 .
 16. 若一次函数( , 是常数)和( , 是常数)图象相交于点 , 则式子的值是 .17. 关于函数的图象,有如下说法:①图象过点;②图象与x轴的交点的坐标为;③y随x的增大而增大;④图象不经过第一象限;⑤图象是与直线平行的直线.其中正确的是(填序号)18. 在平面直角坐标中,点、 , 直线与线段AB有交点,则k的取值范围为 .19. 如图,直线与x轴、y轴分别交于点B与点A, , 点C是直线AB上的一点,且位于第二象限,当△OBC的面积为3时,点C的坐标为 .
16. 若一次函数( , 是常数)和( , 是常数)图象相交于点 , 则式子的值是 .17. 关于函数的图象,有如下说法:①图象过点;②图象与x轴的交点的坐标为;③y随x的增大而增大;④图象不经过第一象限;⑤图象是与直线平行的直线.其中正确的是(填序号)18. 在平面直角坐标中,点、 , 直线与线段AB有交点,则k的取值范围为 .19. 如图,直线与x轴、y轴分别交于点B与点A, , 点C是直线AB上的一点,且位于第二象限,当△OBC的面积为3时,点C的坐标为 . 20. 把8个边长为1的正方形按如图所示摆放在直角坐标系中,经过原点O的直线l将这8个正方形分成面积相等的两部分,则该直线的函数表达式是 .
20. 把8个边长为1的正方形按如图所示摆放在直角坐标系中,经过原点O的直线l将这8个正方形分成面积相等的两部分,则该直线的函数表达式是 .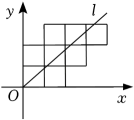
三、解答题(共6题,共60分)
-
21. 将正比例函数的图象平移后经过点.(1)、求平移后的函数表达式;(2)、求平移后函数的图象与坐标轴围成的三角形的面积.22. 我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨4元,超过6吨时,超过的部分按每吨5元收费.该市某户居民5月份用水吨,应交水费元.(1)、请写出与的函数关系式.(2)、如果该户居民这个月交水费34元,那么这个月该户用了多少吨水?23. 如图,已知一次函数y=kx+k+1的图象与一次函数y=-x+4的图象交于点A(1,a).
 (1)、求a、k的值;(2)、根据图象,写出不等式-x+4>kx+k+1的解;(3)、结合图形,当x>2时,求一次函数y=-x+4函数值y的取值范围;24. 如图,直线的函数关系式为 , 且与x轴交于点D,直线经过点 , , 直线与交于点C.
(1)、求a、k的值;(2)、根据图象,写出不等式-x+4>kx+k+1的解;(3)、结合图形,当x>2时,求一次函数y=-x+4函数值y的取值范围;24. 如图,直线的函数关系式为 , 且与x轴交于点D,直线经过点 , , 直线与交于点C. (1)、求直线的函数关系式;(2)、求点C的坐标;(3)、设点P在y轴上,若 , 求点P的坐标.25. 某工厂开发生产一种新产品,设生产的产品数量为(件),总销售额为(元),且与之间满足正比例函数关系,当时,;总成本为(元),与之间关系满足表格:
(1)、求直线的函数关系式;(2)、求点C的坐标;(3)、设点P在y轴上,若 , 求点P的坐标.25. 某工厂开发生产一种新产品,设生产的产品数量为(件),总销售额为(元),且与之间满足正比例函数关系,当时,;总成本为(元),与之间关系满足表格:产品数量(件)
1
2
3
4
总成本(元)
15025
15050
15075
15100
(1)、分别求出、与之间的函数关系式;(2)、设工厂的总利润为(元),求与的函数关系式;(3)、至少生产并销售多少件产品后,工厂才不会亏损.26. 如图,在平面直角坐标系中,一次函数的图象与x轴交于点A,与一次函数的图象交于点B. (1)、求点B的坐标;(2)、结合图象,当时,请直接写出x的取值范围;(3)、C为x轴上点A右侧一个动点,过点C作y轴的平行线,与一次函数的图象交于点D,与一次函数的图象交于点E.当时,求的长.
(1)、求点B的坐标;(2)、结合图象,当时,请直接写出x的取值范围;(3)、C为x轴上点A右侧一个动点,过点C作y轴的平行线,与一次函数的图象交于点D,与一次函数的图象交于点E.当时,求的长.