初中数学同步训练必刷题（人教版八年级下册 19.3 课题学习 选择方案）
试卷更新日期：2023-05-22 类型：同步测试
一、单选题（每题3分，共30分）
-
1. “漏壶”是古代一种计时器，在它内部盛一定量的水，不考虑水量变化对压力的影响，水从壶底小孔均匀漏出，壶内壁有刻度.人们根据壶中水面的位置计算时间.在漏壶漏完水之前，漏壶内水的深度与对应的漏水时间满足的函数关系式（ ）
A、正比例函数关系 B、一次函数关系 C、反比例函数关系 D、二次函数关系2. 弹簧的长度与所挂物体的质量的关系为一次函数，如图所示，由此图可知不挂物体时弹簧的长度为（ ）
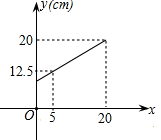A、7cm B、8cm C、9cm D、10cm3. 漏刻是我国古代的一种计时工具，它是中国古代人民对函数思想的创造性应用小明依据漏刻的原理制作了一个简单的漏刻模型研究中发现水位是时间的一次函数，如表是小明记录的部分数据，当时间为时，对应的高度为（ ）1
2
3
2.4
2.8
3.2
A、6.0 B、5.2 C、4.4 D、3.64. 新能源汽车多数采用电能作为动力来源，不需要燃烧汽油，这样就减少了二氧化碳等气体的排放，从而达到保护环境的目的．一辆以电能作为动力来源的新能源汽车剩余的电量百分比y（）与已行驶的路程x（千米）的对应关系如图所示，如果这辆汽车每千米的耗电量相同，当所剩电量百分比为时，该车已行驶的路程为（ ）
A、24千米 B、36千米 C、48千米 D、60千米5. 某市出租车计费办法如图所示．根据图象信息，下列说法错误的是（ ）
A、出租车起步价是10元 B、在3千米内只收起步价 C、超过3千米部分（x＞3）每千米收3元 D、超过3千米时（x＞3）所需费用y与x之间的函数关系式是y=2x+46. 小明同学在一次学科综合实践活动中发现，某品牌鞋子的长度y cm与鞋子的码数x之间满足一次函数关系，下表给出y与x的一些对应值：码数x
26
30
34
42
长度y cm
18
20
22
26
根据小明的数据，可以得出该品牌38码鞋子的长度为（ ）
A、24cm B、25cm C、26cm D、38cm7. 在物理实验课上，小鹏利用滑轮组及相关器材进行实验，他把得到的拉力和所悬挂物体的重力的几组数据用电脑绘制成如下图象（不计绳重和摩擦），请你根据图象判断以下结论正确的序号有（ ）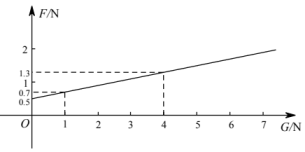
①物体的拉力随着重力的增加而增大；②当物体的重力N时，拉力N；③拉力F与重力G成正比例函数关系；④当滑轮组不悬挂物体时，所用拉力为0.5N．
A、①② B、②④ C、①④ D、③④8. 如图，欣欣妈妈在超市购买某种水果所付金额y（元）与购买x（千克）之间的关系如图所示，则“一次性购买6千克这种水果”比“分2次每次购买3千克这种水果”可节省（ ）元．
A、4 B、3 C、2 D、19. 甲、乙是由两组一模一样的三个圆柱组合而成的容器，现匀速地向两容器注水至满，在注水过程中，甲、乙两容器水面高度h随时间t的变化规律如图所示，则实线对应的容器的形状和A点的坐标分别是（ ）
A、甲，（ ， 3） B、甲，（ ， ） C、乙，（ ， 3） D、乙，（ ， ）10. 武鸣今年沃柑大丰收，希望育才中学初三年级开展了“双减”下劳动实践活动.同学们先从教室出发到果园摘果，再按原路返回教室，同学们离教室的距离y（单位：m）与所用时间t（单位：min）之间的函数关系如图所示，下列说法错误的是（ ）
A、教室距离果园 B、从教室去果园的平均速度是 C、在果园摘果耗时 D、从果园返回教室的平均速度是二、填空题（每空3分，共27分）
-
11. 某文具店购进一批纪念册，每本进价为20元，在销售过程中发现，该纪念册每周的销量y（本）与每本的售价x（元）之间满足一次函数关系： ． 已知某一周该纪念册的售价为每本30元，那么这一周的盈利是元．12. 某种气体的体积y (L)与气体的温度x (C)对应值如下表．若要使气体的体积至少为106升，则气体的温度不低于℃．
x(℃)
……
0
1
2
3
……
10
……
y(L)
……
100
100.3
100.6
100.9
……
103
……
13. 某人购进一批苹果到集贸市场零售，已知卖出的苹果数量y（千克）与售价x（元/千克）之间的关系如图所示，成本为5元/千克，现以8元/千克的价格卖出，挣得元.（用含k的式子表示）
14. 如图，折线表示从甲地向乙地打电话所需的电话费（元）关于通话时间（分钟）的函数图象，则通话7分钟需要支付电话费元．
15. 如图是某旅行车旅客携带行李收费示意图，小李所携带的行李重20千克，那么小李应该交费（元）．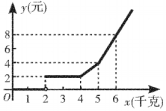
16. 已知A，B两地相距120km，甲、乙两人沿同一条公路从A地出发到B地，甲骑摩托车，乙骑自行车．图中 ， 分别表示甲，乙离开A地的路程s（km）与时间t（h）的函数关系，则乙出发小时被甲追上．
17. 声音在空气中的传播速度v（m／s）与温度t（℃）的关系如下表：温度t（℃）
0
5
10
15
20
速度v（m／s）
331
336
341
346
351
当t＝30 ℃时，声音的传播速度为m/s．
18. 某手工作坊生产并销售某种食品，假设销售量与产量相等，如图中的线段AB、OC分别表示每天生产成本（单位：元）、收入（单位：元）与产量x（单位：千克）之间的函数关系.若该手工作坊某一天既不盈利也不亏损，则这天的产量是千克.
19. 一食堂需要购买盒子存放食物，盒子有A，B两种型号，单个盒子的容量和价格如表，现有15升食物需要存放且要求每个盒子要装满.由于A型号盒子正在做促销活动：购买三个及三个以上可一次性返现金4元，则购买盒子所需要最少费用为元.型号
A
B
单个盒子容量（升)
2
3
单价（元)
5
6
三、解答题（共6题，共63分）
-
20. 为了落实劳动教育，某学校邀请农科院专家指导学生进行小番茄的种植，经过试验，其平均单株产量千克与每平方米种植的株数构成一种函数关系每平方米种植2株时，平均单株产量为4千克；以同样的栽培条件，每平方米种植的株数每增加1株，单株产量减少0.5千克.(1)、求关于的函数表达式；(2)、每平方米种植多少株时，能获得的产量？21. 为了学生的身体健康，学校新进了一批课桌椅，可以根据人的身高调节高度，配套课桌椅的高度都是按一定的关系科学设计的.桌椅的高度配套时，以每档的椅高的值为横坐标，桌高的值为纵坐标，在平面直角坐标系中描点如图：
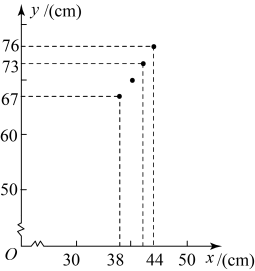(1)、你认为桌高y与椅高x满足什么函数关系？请你求出这个函数的关系式（不要求写出x的取值范围）.(2)、小明测量了自己新更换的课桌椅，桌子的高度为 ， 椅子的高度为 ， 请你判断它们是否配套？如果配套，说明理由；如果不配套，请说明可以如何调整桌子或椅子的高度使得它们配套.22. 小米手机越来越受到大众的喜爱，各种款式相继投放市场，某店经营的A款手机去年销售总额为50000元，今年每部销售价比去年降低400元，若卖出的数量相同，销售总额将比去年减少 ．A，B两款手机的进货和销售价格如下表：
A款手机
B款手机
进货价格元
1100
1400
销售价格元
今年的销售价格
2000
(1)、今年A款手机每部售价多少元？(2)、该店计划新进一批A款手机和B款手机共60部，且B款手机的进货数量不超过A款手机数量的两倍，应如何进货才能使这批手机获利最多？23. 学校计划组织初二年级200名师生到红军烈士陵园举行清明扫墓纪念活动.现需租用A，B两种型号的客车共10辆，两种型号客车的载客量（不包括司机）和租金信息如下表：型号
载客量（人/辆）
租金单价（元/辆）
A
16
900
B
22
1200
若设租用A型客车x辆，租车总费用为y元.
(1)、请写出y与x的函数关系式（不要求写自变量取值范围）：(2)、据资金预算，本次租车总费用不超过11800元，则A型客车至少需租几辆？(3)、在（2）的条件下，要保证全体师生都有座位，问有哪几种租车方案？请选出最省钱的租车方案.24. 在中小学生科技节中，某校展示了学生自主研制的甲、乙两种电动车搬运货物的能力．这两种电动车充满电后都可以连续搬运货物30分钟．甲种电动车先开始搬运，6分钟后，乙种电动车开始搬运．线段、分别表示两种电动车的搬运货物量（千克）与时间（分）（从甲种电动车开始搬运时计时）的函数图象，根据图象提供的信息，解答下列问题：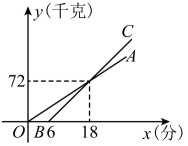
(1)、甲种电动车每分钟搬运货物量为千克，乙种电动车每分钟笒运货物量为千克．(2)、当时，求乙种电动车的搬运货物量（千克）与时间（分）之间的函数关系式．(3)、在甲、乙两车同时搬运货物的过程中，直接写出二者搬运量相差8千克时的值．25. “地摊经济”成为社会关注的热门话题，小明从市场得知如下信息：甲商品
乙商品
进价（元/件）
65
5
售价（元/件）
90
10
小明计划购进甲、乙商品共100件进行销售，设小明购进甲商品件，甲、乙商品全部销售完后获得利润为元．
(1)、求出与之间的函数关系式，并写出的取值范围．(2)、小明用不超过3500元资金一次性购进甲、乙两种商品，求的取值范围．(3)、在（2）的条件下，若要求甲，乙商品全部销售完后获得的利润不少于1450元，请说明小明有哪些可行的进货方案，并计算哪种进货方案的利润最大，最大利润是多少？