鲁教版(五四制)2022-2023学年度第二学期七年级数学 二元一次方程与一次函数 期末复习
试卷更新日期:2023-05-22 类型:复习试卷
一、单选题
-
1. 如图,在平面直角坐标系xOy中,若直线与直线相交于点P,则下列结论中:
①;
②当时,;
③关于x,y的方程组的解是;
所有正确结论的序号是( )
 A、①② B、②③ C、①③ D、①②③2. 如图,经过点和经过原点和点 , 以两条直线的交点坐标为解的方程组是( )
A、①② B、②③ C、①③ D、①②③2. 如图,经过点和经过原点和点 , 以两条直线的交点坐标为解的方程组是( ) A、 B、 C、 D、3. 如图,已知一次函数的图象与轴,轴分别交于点 , , 与正比例函数交于点 , 已知点的横坐标为2,以下结论:①关于的方程的解为:②对于直线 , 当时,:③对于直线 , 当时,:④方程组的解为 , 其中正确的有( )个
A、 B、 C、 D、3. 如图,已知一次函数的图象与轴,轴分别交于点 , , 与正比例函数交于点 , 已知点的横坐标为2,以下结论:①关于的方程的解为:②对于直线 , 当时,:③对于直线 , 当时,:④方程组的解为 , 其中正确的有( )个 A、1 B、2 C、3 D、44. 用图象法解二元一次方程组时,小英所画图象如图所示,则方程组的解为( )
A、1 B、2 C、3 D、44. 用图象法解二元一次方程组时,小英所画图象如图所示,则方程组的解为( ) A、 B、 C、 D、5. 在同一平面直角坐标系中,函数与的图象的交点坐标为( )A、 B、 C、 D、6. 如图,直线与直线相交于点 , 则关于 , 的方程组( )
A、 B、 C、 D、5. 在同一平面直角坐标系中,函数与的图象的交点坐标为( )A、 B、 C、 D、6. 如图,直线与直线相交于点 , 则关于 , 的方程组( ) A、 B、 C、 D、7. 如图,过点A的一次函数的图象与正比例函数y=2x的图象相交于点B , 则这个一次函数的解析式是( )
A、 B、 C、 D、7. 如图,过点A的一次函数的图象与正比例函数y=2x的图象相交于点B , 则这个一次函数的解析式是( )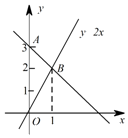 A、y=2x+3 B、y=x﹣3 C、y=2x﹣3 D、y=﹣x+38. 如图,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x , x的二元一次方程组 的解,那么这个点是( )
A、y=2x+3 B、y=x﹣3 C、y=2x﹣3 D、y=﹣x+38. 如图,在平面直角坐标系xOy中,如果一个点的坐标可以用来表示关于x , x的二元一次方程组 的解,那么这个点是( )
 A、M B、N C、E D、F9. 一次函数y=kx+b与y=x+2的图象相交于如图点P(m , 4),则关于x , y的二元一次方程组 的解是( )
A、M B、N C、E D、F9. 一次函数y=kx+b与y=x+2的图象相交于如图点P(m , 4),则关于x , y的二元一次方程组 的解是( ) A、 B、 C、 D、10. 一般地,在平面直角坐标系中,任何一个二元一次方程的解可以看成是一个点的坐标,那么,以二元一次方程的解为坐标的点的全体叫做这个二元一次方程的图象.根据作图我们发现:任何一个二元一次方程的图象都是一条直线.根据这个结论,如图,如果一个点的坐标可以用来表示关于x、y的二元一次方程组 的解,那么这个点是( )
A、 B、 C、 D、10. 一般地,在平面直角坐标系中,任何一个二元一次方程的解可以看成是一个点的坐标,那么,以二元一次方程的解为坐标的点的全体叫做这个二元一次方程的图象.根据作图我们发现:任何一个二元一次方程的图象都是一条直线.根据这个结论,如图,如果一个点的坐标可以用来表示关于x、y的二元一次方程组 的解,那么这个点是( ) A、M B、N C、E D、F
A、M B、N C、E D、F二、填空题
-
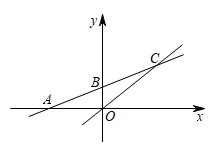
11. 如图,在同一直角坐标系中作出一次函数y=k1x与y=k2x+b的图象,则二元一次方程组的解是
 12. 如图,直线与直线相交于点 , 则方程组的解为 .
12. 如图,直线与直线相交于点 , 则方程组的解为 .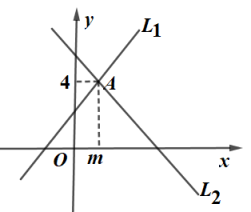 13. 已知直线y=2x﹣3向上平移3个单位后,得到的直线的解析式为 .14. 如图,函数y=ax+b和y=kx的图象交于一点,则二元一次方程组 的解是 .
13. 已知直线y=2x﹣3向上平移3个单位后,得到的直线的解析式为 .14. 如图,函数y=ax+b和y=kx的图象交于一点,则二元一次方程组 的解是 .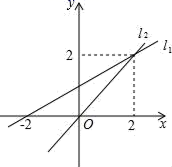 15. 直线 与 的图象如图所示,则方程组 的解是 .
15. 直线 与 的图象如图所示,则方程组 的解是 .
三、解答题
-
16. 如图,直线与x轴交于点 , 与y轴交于点B,与直线交于点 . 若要在y轴找到一个点P使得的面积为15,求这个点P的坐标.
 17. 已知直线与直线交于点A,点A的横坐标为4,且直线经过点 , 求k,b的值.18. 如图所示,直线 , 相交于A点,请根据图象求出直线 , 的解析式,并直接写出以交点A的坐标为解的二元一次方程组的解.
17. 已知直线与直线交于点A,点A的横坐标为4,且直线经过点 , 求k,b的值.18. 如图所示,直线 , 相交于A点,请根据图象求出直线 , 的解析式,并直接写出以交点A的坐标为解的二元一次方程组的解.
四、综合题
-
19. 阅读材料,回答以下问题:
我们知道,二元一次方程有无数个解,在平面直角坐标系中,我们标出以这个方程的解为坐标的点,就会发现这些点在同一条直线上.例如是方程的一个解,对应点 , 如图所示,我们在平面直角坐标系中将其标出,另外方程的解还有对应点 , , , , 将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程的解.所以,我们就把这条直线就叫做方程的图象.一般的,以任意二元一次方程解为坐标的对应点连成的直线就叫这个方程的图象.请问:
 (1)、已知、、 , 则点(填“或或”)在方程的图象上.(2)、求方程和方程图象的交点坐标.(3)、已知以关于、的方程组的解为坐标的点在方程的图象上,求的值.20. 在平面直角坐标系中,直线y=-x+与y=x+3交于点A,
(1)、已知、、 , 则点(填“或或”)在方程的图象上.(2)、求方程和方程图象的交点坐标.(3)、已知以关于、的方程组的解为坐标的点在方程的图象上,求的值.20. 在平面直角坐标系中,直线y=-x+与y=x+3交于点A, (1)、求点A的坐标;(2)、根据图象直接写出不等式-x+>x+3的解集21. 如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=x﹣4交于D,C为直线CD与y轴的交点,求:
(1)、求点A的坐标;(2)、根据图象直接写出不等式-x+>x+3的解集21. 如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=x﹣4交于D,C为直线CD与y轴的交点,求: (1)、直线AB对应的函数表达式;(2)、求S△ADC.22. 如图,一次函数 经过点 ,与一次函数 交于点 .
(1)、直线AB对应的函数表达式;(2)、求S△ADC.22. 如图,一次函数 经过点 ,与一次函数 交于点 . (1)、求函数 的表达式;(2)、利用函数图象写出方程组 的解 .23. 阅读材料,回答以下问题:
(1)、求函数 的表达式;(2)、利用函数图象写出方程组 的解 .23. 阅读材料,回答以下问题:一般地,一个二元一次方程的解有无数个,且每个解都指满足方程的一对数值,而不是指单独的一个未知数的值.例如:二元一次方程的解有 , , ……
在平面直角坐标系中(如图),我们标出以这个方程的解为坐标的一些点(其中的值为横坐标,的值为纵坐标),如 , , ……就会发现如果将这些点连起来正好是一条直线,也就是说这些点都在同一条直线上;反过来,在这条直线上任意选取一点,比如 , 将这个点的坐标作为一对未知数的值即代入方程中,发现它即为该方程的一个解.这样,二元一次方程的所有解与这条直线上的所有点就建立了一一对应关系,我们把这条直线就叫做方程的图象.一般地,任意二元一次方程解的对应点连成的直线就叫这个方程的图象.请问:
 (1)、已知 , , , 其中点(填“或或”)在方程的图象上.(2)、由上述阅读材料可知,一个二元一次方程的图象是一条直线,画它的图象至少需要描出 ▲ 个点.请在如图所示的平面直角坐标系中画出方程和的图象;
(1)、已知 , , , 其中点(填“或或”)在方程的图象上.(2)、由上述阅读材料可知,一个二元一次方程的图象是一条直线,画它的图象至少需要描出 ▲ 个点.请在如图所示的平面直角坐标系中画出方程和的图象; (3)、通过观察可知这两条直线的位置关系是 , 由此猜想:两条直线位置关系和方程组的解之间一定存在某种联系,有可能是 .
(3)、通过观察可知这两条直线的位置关系是 , 由此猜想:两条直线位置关系和方程组的解之间一定存在某种联系,有可能是 .