初中数学同步训练必刷题（人教版八年级下册 19.2 一次函数）

试卷更新日期：2023-05-22 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列函数① $y = - 5 x$ ；② $y = - 2 x + 1$ ；③ $y = \frac{3}{x}$ ；④ $y = \frac{1}{2} x - 1$ ；⑤ $y = x^{2} - 1$ 中，是一次函数的有（）．

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 直线 $y = 3 x - 6$ 与x轴的交点坐标是（）．

A、 $(2 ， 0)$ B、 $(0 ， 2)$ C、 $(0 ， - 6)$ D、 $(- 6 ， 0)$

查看试题解析
3. 若一次函数的 $y = - 3 x + b$ 图象上有两点 $A (- 2 ， y_{1})$ ， $B (6 ， y_{2})$ ，则下列 $y_{1}$ ， $y_{2}$ 大小关系正确的是（）．

A、 $y_{1} > y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} \geq y_{2}$ D、 $y_{1} \leq y_{2}$

查看试题解析
4. 将一次函数y＝-2x的图象沿y轴向下平移4个单位长度后，所得图象的函数表达式为（）

A、y＝-2（x-4） B、y＝-2x+4 C、y＝-2（x+4） D、y＝-2x-4

查看试题解析
5. 已知 $P (- 2 ， 4)$ ， $Q (3 ， - 6)$ ， $R$ $(1 ， - 2)$ ， $S (- 2 ， 6)$ 中有三个点在同一直线 $y = k x$ 上，不在此直线上的点是（）

A、点 $P$ B、点 $Q$ C、点 $R$ D、点 $S$

查看试题解析
6. 在平面直角坐标系中，函数 $y = k x + b$ 的图象如图所示，则下列判断正确的是（　　）

A、 $k > 0$ B、 $b < 0$ C、 $k \cdot b > 0$ D、 $k \cdot b < 0$

查看试题解析
7. 在同一平面直角坐标系中，函数y＝kx与 $y = \frac{1}{2} x - k$ 的图像大致是（）

A、 B、 C、 D、

查看试题解析
8. 已知一次函数 $y = k x + b$ 与 $y = m x + n$ 的图象如图所示，若 $k x + b > m x + n$ ，则x的取值范围为（）

A、 $x > 2$ B、 $x < 2$ C、 $x > - 2$ D、 $x < - 2$

查看试题解析
9. 同一平面直角坐标系中，一次函数 $y = k_{1} x + b$ 的图象与 $y = k_{2} x$ 的图象如图所示，则关于x的方程 $k_{1} x + b = k_{2} x$ 的解为（）

A、 $x = 0$ B、 $x = - 1$ C、 $x = - 2$ D、以上都不对

查看试题解析
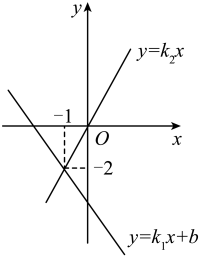10. 如图，是某工程队修路的长度y（单位：m）与修路时间t（单位：天）之间的函数关系．该工程队承担了一项修路任务，任务进行一段时间后，工程队提高了工作效率，则该工程队提高效率前每天修路的长度是（）米．

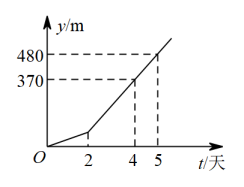A、150 B、110 C、75 D、70

查看试题解析

二、填空题（每空3分，共30分）

11. 请写出一个图象经过第一、二、四象限且与y轴交于点（0，1）的一次函数的解析式 .

查看试题解析
12. 函数 $y = (m - 2) x ＋ 2$ 是关于 $x$ 的一次函数，则 $m$ 满足的条件是.

查看试题解析
13. 将直线 $y = 4 x + 3$ 向下平移2个单位长度，平移后直线的解析式为．

查看试题解析
14. 已知正比例函数 $y = k x$ 的图象经过第二、四象限，若点 $A (1 ， a) ， B (- 1 ， b)$ 在该函数的图象上，则ab.（填“>”“<”或“=”）

查看试题解析

15. 在画一次函数

y = kx + b

的图象时，小雯同学列表如下，其中“

▲

”表示的数为

$x$	$\dots$	-2	-1	0	1	2	$\dots$
$y$	$\dots$	5	3	1	$▲$	-3	$\dots$

查看试题解析

16. 已知点 $A (a ， b)$ 在一次函数 $y = 2 x - 1$ 图象上，则 $a^{2} + b + 3$ 的最小值为．

查看试题解析
17. 已知一次函数 $y = x - 3$ 与 $y = k x$ （k是常数， $k \neq 0$ ）的图像的交点坐标是 $(2 ， - 1)$ ，则方程组 ${\begin{array}{l} x - y = 3 \\ k x - y = 0 \end{array}$ 的解是.

查看试题解析
18. 如图，一次函数 $y = k x + b$ 的图象经过点 $(4 ， - 3)$ ，则关于x的不等式 $k x + b \geq - 3$ 的解集为 .

查看试题解析
19. 为了加强公民的节水意识，我市制定了如下用水收费标准：每户每月的用水不超过 $10$ 吨时，水价为每吨 $1.5$ 元；超过 $10$ 吨时，超过的部分按每吨 $2$ 元收费．现有某户居民 $5$ 月份用水 $x (x > 10)$ 吨，应交水费 $y$ 元，则 $y$ 关于 $x$ 的函数关系式是．

查看试题解析
20. 小泽和小帅两同学分别从甲地出发，骑自行车沿同一条路到乙地参加社会实践活动．如图折线 $O A B$ 和线段 $C D$ 分别表示小泽和小帅离甲地的距离y（单位：千米）与时间x（单位：小时）之间函数关系的图象，则当小帅到达乙地时，小泽距乙地的距离为千米．

查看试题解析

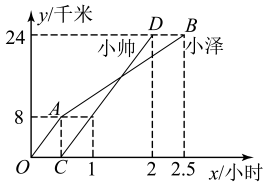
三、解答题（共6题，共60分）

21. 如图所示，表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程y(千米)随时间t（时）变化的图象，根据图象回答下列问题

(1)、轮船的行驶速度是km/h；

(2)、当2≤t≤6时，求快艇行驶过程y与t的函数关系式；

(3)、当快艇与乙港相距40 km时，快艇和轮船相距km

查看试题解析
22. 如图，在平面直角坐标系 $x O y$ 中，正比例函数 $y = x$ 的图象与一次函数 $y = k x - k$ 的图象的交点坐标为 $A (m ， 2)$ .

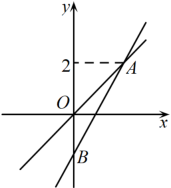(1)、求m的值和一次函数的解析式；

(2)、直接写出使函数 $y = k x - k$ 的值大于函数 $y = x$ 的值的自变量x的取值范围.

查看试题解析
23. 如图，一次函数 $y = k_{2} x + b$ 的图象与y轴交于点B，与正比例函数 $y = k_{1} x$ 的图象相交于点 $A (3 ， 4)$ ，且 $O A = O B$ .

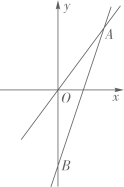(1)、分别求出这两个函数的解析式；

(2)、求 $Δ A O B$ 的面积；

(3)、点P在x轴上，且 $Δ P O A$ 是等腰三角形，请直接写出点P的坐标.

查看试题解析
24. 甲、乙两家旅行社推出家庭旅游优惠活动，两家旅行社的票价均为每人90元，但优惠的办法不同．甲旅行社的优惠是：全家有一人购全票，其余人半价优惠；乙旅行社的优惠是：全家按六折优惠．设某一家庭共有x人，甲、乙两家旅行社的收费分别是 $y_{1}$ 、 $y_{2}$ 元．

(1)、求 $y_{1}$ 、 $y_{2}$ 与x之间的函数关系式；

(2)、请根据不同家庭的人数情况，说明选择哪家旅行社的费用较低？

查看试题解析
25. 如图，直线y＝- $\frac{1}{2}$ x+b与x轴，y轴分别交于A，B两点，点A的坐标为（6，0）.在x轴的负半轴上有一点C（-4，0），直线AB上有一点D，且CD＝OD.

(1)、求b的值及点D的坐标；

(2)、在线段AB上有一个动点P，点P的横坐标为a，作点P关于y轴的对称点Q，当点Q落在△CDO内（不包括边界）时，求a的取值范围.

查看试题解析
26. 如图，直线 $l_{1} ： y = - 2 x + 4$ 分别与x轴、y轴交于A，B两点，直线 $l_{2}$ 与 $l_{1}$ 交于点 $P (a ， 2)$ ，与x轴交于点 $C (- 3 ， 0)$ ，点M在线段 $A B$ 上，直线 $M E ⊥ x$ 轴于点E，与 $l_{2}$ 交于点N．

(1)、求直线 $l_{2}$ 的表达式；

(2)、设点M的横坐标为m．
①当 $m = \frac{3}{2}$ 时，求线段 $M N$ 的长；
②若点M，N，E三点中，其中两点恰好关于第三点对称，直接写出此时m的值．

查看试题解析