人教版七年级下数学期末复习知识点扫盲满分计划——9.2一元一次不等式
试卷更新日期:2023-05-22 类型:复习试卷
一、一元一次不等式的定义:含有1个未知数,其次数是1的不等式
-
1. 若是关于的一元一次不等式,则的值为 .2. 若是关于的一元一次不等式.则的值为( )A、2 B、-1 C、0 D、0或23. 若是关于x的一元一次不等式,则该不等式的解集是 .4. 已知是关于x的一元一次不等式,则m的值为 .5. 下列不等式中,一元一次不等式有 ( )
① ② ③
④ ⑤
A、 个 B、 个 C、 个 D、 个二、求一元一次不等式的解集:大右小左,有等实心无等空
-
6. 不等式的解集在数轴上表示正确的是( )A、
 B、
B、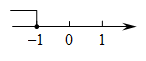 C、
C、 D、
D、 7. 不等式的解集为 .8. 不等式的解集在数轴上表示正确的是( )A、
7. 不等式的解集为 .8. 不等式的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、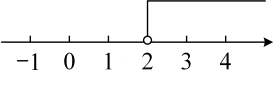 D、
D、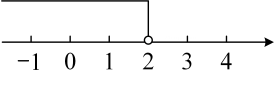 9. 在-2,-1,0,1,2这五个数中,是不等式解的共有( )A、1个 B、2个 C、3个 D、4个10. 解下列不等式:(1)、;(2)、.
9. 在-2,-1,0,1,2这五个数中,是不等式解的共有( )A、1个 B、2个 C、3个 D、4个10. 解下列不等式:(1)、;(2)、.三、一元一次整数解:整数包括负整数、0、正整数
-
11. 已知方程 , 且关于x的不等式只有2个整数解,那么b的取值范围是( )A、 B、 C、 D、12. 关于x的不等式:有3个负整数解,则a的取值范围是( )A、 B、 C、 D、13. 不等式的非负整数解为.14. 当 x取何正整数值时, 代数式 与 的值的差大于1.15. 满足不等式2(2x-4)>-3x+6的最小整数是.
四、求一元一次不等式的最值
-
16. 已知关于的方程 ,(1)、若该方程的解满足 , 求的取值范围;(2)、若该方程的解是不等式的最小整数解,求的值.17. 已知关于x的不等式只有两个负整数解,则a的取值范围是( )A、 B、 C、 D、18. 不等式的最大整数解是 .19. 满足不等式的最小整数是 .20. 关于 x 的不等式 x﹣k ≤ 0 的正整数解是1、2,那么k的最小值是.
五、列一元一次不等式
-
21. 若代数式的值不大于6,则可列不等式为: .22. “的3倍与2的差不小于9”列出的不等式是 .23. a与b的差是非负数,列出不等式为 .24. “a的3倍与5的差不小于8”用不等式表示为 .25. 下列语句中,正确的是( )A、小朋还不到十五岁,设小明岁,则有 B、甲数的三倍比乙数大4个单位,则有 C、某数是非负数,则有 D、卡车载重限重5吨,设卡车载重y吨,则有
六、含绝对值的不等式
-
26. 阅读下面材料:
小明在数学课外小组活动时遇到这样一个问题:
如果一个不等式中含有绝对值,并且绝对值符号中含有未知数,我们把这个不等式叫做绝对值不等式,求绝对值不等式 的解集.
小明同学的思路如下:
先根据绝对值的定义,求出 恰好是 时 的值,并在数轴上表示为点 ,如图所示.观察数轴发现,以点 为分界点把数轴分为三部分:
点 左边的点表示的数的绝对值大于 ;
点 之间的点表示的数的绝对值小于 ;
点 右边的点表示的数的绝对值大于 .
因此,小明得出结论绝对值不等式 的解集为: 或 .
参照小明的思路,解决下列问题:
(1)、请你直接写出下列绝对值不等式的解集.① 的解集是 .
② 的解集是 .
(2)、求绝对值不等式 的解集.(3)、如果(2)中的绝对值不等式的整数解,都是关于 的不等式组 的解,求 的取值范围.(4)、直接写出不等式 的解集是 .27. 在数学课外小组活动中,老师提出了如下问题:如果一个不等式中含有绝对值,并且绝对值符号中含有未知数,我们把这个不等式叫做绝对值不等式,求绝对值不等式|x|>a(a>0)和|x|<a(a>0)的解集.
小明同学的探究过程如下:
先从特殊情况入手,求|x|>2和|x|<2的解集.确定|x|>2的解集过程如下:
先根据绝对值的几何定义,在数轴上找到到原点的距离大于2的所有点所表示的数,在数轴上确定范围如下:
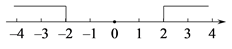 (1)、请将小明的探究过程补充完整;
(1)、请将小明的探究过程补充完整;所以,|x|>2的解集是x>2或 .
再来确定|x|<2的解集:同样根据绝对值的几何定义,在数轴上找到到原点的距离小于2的所有点所表示的数,在数轴上确定范围如下:
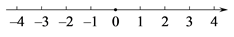
所以,|x|<2的解集为: .
经过大量特殊实例的实验,小明得到绝对值不等式|x|>a(a>0)的解集为 , |x|<a(a>0)的解集为 .
请你根据小明的探究过程及得出的结论,解决下列问题:
(2)、求绝对值不等式2|x+1|-3<5的解集.28. 阅读下列材料:小明在一本数学杂志上看到一道有意思的数学题:解不等式 , 根据绝对值的几何意义,到原点距离小于1的点在数轴上集中在-1和+1之间,如图:

所以,该不等式的解集为 .
因此,不等式的解集为或 .
根据以上方法小明继续探究了不等式的解集,即到原点的距离大于2小于5的点的集合就集中在这样的区域内,如图:

所以,不等式的解集为-5<x<-2或2<x<5.
仿照小明的做法解决下面问题:
(1)、不等式的解集为;(2)、不等式的解集是;(3)、不等式的解集是 .29. 阅读下列材料并解答问题:我们知道 的几何意义是在数轴上数 对应的点与原点的距离: ,也就是说, 表示在数轴上数 与数0对应点之间的距离;
这个结论可以推广为 表示在数轴上数 和数 对应的点之间的距离;
例1解方程 ,容易看出,在数轴上与原点距离为2的点对应的数为 ,即该方程的解为 .
例2解不等式 ,如图,在数轴上找出 的解,即到1的距离为2的点对应的数为 ,3,则 的解集为 或 .

例3解方程 由绝对值的几何意义知,该方程表示求在数轴上与1和 的距离之和为5的对应的 的值.在数轴上,1和 的距离为3,满足方程的 对应的点在1的右边或 的左边,若 对应的点在1的右边,由下图可以看出 ;同理,若 对应的点在 的左边,可得 ,故原方程的解是 或 .

回答问题:(只需直接写出答案)
①解方程
②解不等式
③解方程
30. 用不等式表示:的绝对值与1的和大于1.七、一元一次不等式的应用
-
31. 春运期间,某客运站旅客流量不断增大,旅客往往需要很长时间排队等候购票.经调查发现,每天开始售票时,约有400人排队购票.同时又有新的旅客不断进入售票厅排队等候购票,购票时售票厅每分钟新增4人,每分钟每个窗口出售票数张.(规定每人只限购一张)(1)、若开放两个售票窗口,问开始售票后多少分钟售票厅内有320人?(2)、若在开始售票20分钟后,来购票的旅客不用排队等待,至少需要开放几个窗口?32. 某学校社会实践小组组织去湿地保护区参加青少年社会实践项目,该保护区的票价为:20人以下每人10元,20人及以上按八折优惠.(1)、如果预计15~18人去保护区,那么请通过计算说明怎样购票更省钱.(2)、该小组现有500元的活动经费,且每人往返车费3元,则至多可以去多少人?33. 小颖准备用元钱买笔和笔记本.已知每支笔元,每个笔记本元,她买了个笔记本,则她最多还可以买多少支笔?34. 小西在准备爱心易物活动时发现班级同学捐赠的一个布偶的成本为60元,定价为90元,为使得利润率不低于5%,在实际售卖时,该布偶最多可以打( )折.A、八 B、七 C、七五 D、八五35. 某农户为即将丰收的普罗旺斯水果西红柿出售做计划.经调研用下列两种方式同时销售:
①运往市区蔬菜市场销售:已知运往市区蔬菜市场销售每千克售价为10元,平均每天需支付运费及其它各项税费200元(运往蔬菜市场的西红柿都能销售完);
②顾客亲自去采摘购买;顾客亲自去采摘购买每千克售价为8元,不再产生其它费用.在高产的15天,平均每天成熟的西红柿达到300千克.
在这期间该农户计划同时采用以上两种销售方式,若该农户要使这15天销售的西红柿总收入不少于39000元,平均每天应至少运往市区蔬菜市场多少千克西红柿?
八、综合训练
-
36. 若关于x的方程x-m=4的解满足不等式2x+1 >3,则可取的负整数为= .37. 已知关于的不等式x-a≤0的正整数解恰好为1,2,3,则的取值范围是( )A、a≥3 B、3≤a<4 C、3<a≤4 D、3≤a≤438. 若关于x的不等式2﹣m﹣x>0的正整数解共有3个,则m的取值范围是( )A、﹣1≤m<0 B、﹣1<m≤0 C、﹣2≤m<﹣1 D、﹣2<m≤﹣139. 关于x的不等式(其中a为正整数)正整数解为1,2,3,则a的值是 .40. 关于x的不等式x﹣1<a有3个非负整数解,则a的取值范围是( )A、1<a<2 B、1<a≤2 C、1≤a≤2 D、2<a≤341. 已知关于x的一元一次不等式 ,有且只有两个不相等的正整数解,则实数a的取值范围为 .