人教版七年级下数学期末复习知识点扫盲满分计划——8.4三元一次方程组及应用

试卷更新日期：2023-05-21 类型：复习试卷

进入出卷网下载

一、两个方程相关的三元一次方程问题

1. 有甲、乙、丙三种货物，若购甲3件、乙7件、丙1件，共需64元；若购甲4件、乙10件、丙1件，共需79元；现购甲、乙、丙各一件，共需（）元

A、33 B、34 C、35 D、36

查看试题解析
2. 已知x，y，z为实数，满足 ${\begin{array}{l} x + 2 y - z = 6 \\ x - y + 2 z = 3 \end{array}$ ，那么x²+y²+z²的最小值是

查看试题解析
3. 已知实数x，y，z满足 ${\begin{array}{l} x + y + z = 7 \\ 4 x + y - 2 z = 2 \end{array}$ ，则代数式3(x﹣z)+1的值是（）

A、﹣2 B、﹣4 C、﹣5 D、﹣6

查看试题解析
4. 6月18日，最开始是京东的周年庆，2013年后，618就成了各大电商平台的网购节了．在618当日，小梦在某电商平台上选择了甲乙丙三种商品，当购物车内选3件甲，2件乙，1件丙时显示价格为420元；当选2件甲，3件乙，4件丙时显示价格为580元，那么购买甲、乙、丙各两件时应该付款（）

A、200元 B、400元 C、500元 D、600元

查看试题解析
5. 小华和小盘到校门外文具店买文件，小华购铅笔2支，练习本2本，圆珠笔1支，共付9元钱；小慧购同样铅笔1支，练习本4本，圆珠笔2支，共付12元钱，若小明去买与她们一样的购铅笔1支、练习本2本、圆珠笔1支，他需付元钱.

查看试题解析

二、含有比值的三元一次方程的解法

6. 已知方程组 ${\begin{matrix} \frac{x}{2} = \frac{y}{3} = \frac{z}{4} \\ 5 x - 2 y + z = 16 \end{matrix}$ 若设 $\frac{x}{2} = \frac{y}{3} = \frac{z}{4} =k$ ，则k= ．

查看试题解析
7. 若x＋y＋z≠0且 $\frac{2 y + z}{x} = \frac{2 x + y}{z} = \frac{2 z + x}{y} = k$ ，则k＝．

查看试题解析
8. ${\begin{matrix} x ： y ： z = 1 ： 3 ： 5 \\ x + y + z = 18 \end{matrix}$

查看试题解析
9. ${\begin{matrix} \frac{x}{3} = \frac{y}{2} = \frac{z}{5} \\ 2 x + 3 y - 4 z = 8 \end{matrix}$

查看试题解析
10. 解方程组
${\begin{matrix} \frac{x}{2} = \frac{y}{3} = \frac{z}{4} \\ 5 x + 2 y - 3 z = 8 \end{matrix}$

查看试题解析

三、三个二元一次方程组成的三元一次方程组

11. 若 ${\begin{cases} x + y = 27 \\ y + z = 33 \\ z + x = 30 \end{cases}$ ，则代数式x+y+z的值为．

查看试题解析
12. 三元一次方程组 ${\begin{array}{l} x + y = 7 \\ x - z = 15 \\ 2 x + z = 6 \end{array}$ 的解是.

查看试题解析
13. 方程组 ${\begin{array}{l} x + y = - 1 \\ x + z = 0 \\ y + z = 1 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = - 1 \\ y = 1 \\ z = 0 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 0 \\ z = - 1 \end{array}$ C、 ${\begin{array}{l} x = 0 \\ y = 1 \\ z = 1 \end{array}$ D、 ${\begin{array}{l} x = - 1 \\ y = 0 \\ z = 1 \end{array}$

查看试题解析
14. 已知方程组 ${\begin{array}{l} x + y = 3 \\ y + z = - 2 \\ z + x = 9 \end{array}$ ，则x＋y＋z的值为（）

A、6 B、－6 C、5 D、－5

查看试题解析
15. 三元一次方程组 ${\begin{array}{l} x + y = 10 \\ y + z = 20 \\ z + x = 40 \end{array}$ 的解是．

查看试题解析

四、坡路问题

16. 小明从家到学校的路程为3.3千米，其中有一段上坡路，平路，和下坡路．如果保持上坡路每小时行3千米．平路每小时行4千米，下坡路每小时行5千米．那么小明从家到学校用一个小时，从学校到家要44分钟，求小明家到学校上坡路、平路、下坡路各是多少千米？

查看试题解析
17. 汽车在平路上每小时行30千米，上坡时每小时行28千米，下坡时每小时行35千米，现在行驶142千米的路程用去4小时30分钟，回来使用4小时42分钟，问这段路中平路有多少千米？去时上、下坡各有多少千米？

查看试题解析
18. 汽车在平路、上坡路、下坡路的速度分别为30km/h，28km/h，35km/h，甲、乙两地两距142km，汽车从甲地去乙地需4.5h，从乙地回甲地需4.7h．从甲地去乙地，平路、上坡路、下坡路各有多少千米？

查看试题解析

五、三元一次方程的应用

19. 某超市销售糖果，将 $A$ 、 $B$ 、 $C$ 三种糖果搭配成甲、乙、丙三种礼盒方式销售，每个礼盒的成本分别为礼盒中 $A$ 、 $B$ 、 $C$ 糖果的成本之和，礼盒成本忽略不计.甲种礼盒每盒分别装有 $A$ 、 $B$ 、 $C$ 三种糖果 $7 k g$ 、 $2 k g$ 、 $1 k g$ ，乙种礼盒每盒分别装有 $A$ 、 $B$ 、 $C$ 三种糖果 $1 k g$ 、 $6 k g$ 、 $3 k g$ ，每盒甲的成本是每千克 $A$ 成本的12倍，每盒甲的销售利润率为25%，每盒甲的售价比每盒乙的售价低 $\frac{1}{6}$ ，丙每盒在成本上提高30%标价后打九折销售获利为每千克 $A$ 成本的1.7倍，当销售甲、乙、丙三种礼盒的数量之比为 $2 ： 1 ： 4$ 时，销售的总利润率为.（用百分数表示）

查看试题解析
20. 一个三位数，百位上的数与十位上的数之差是2，如果交换十位数字与个位数字的位置，那么所得的数就比原来小36，则百位上的数与个位上的数之差为（）

A、5 B、6 C、7 D、8

查看试题解析
21. 《孙子算经》中有一个问题：今有甲、乙、丙三人持钱 .甲语乙、丙：“各将公等所持钱半以益我，钱成九十 .”乙复语甲、丙：“各将公等所持钱半以益我，钱成七十 .”丙复语甲、乙：“各将公等所持钱半以益我，钱成五十六 .”若设甲、乙各持钱数为x、y，则丙持钱数不可以表示为（）

A、 $56 - \frac{x}{2} - \frac{y}{2}$ B、 $180 - 2 x - y$ C、 $140 - 2 x - y$ D、 $140 - x - 2 y$

查看试题解析
22. 重庆一中趣味数学社团在社团活动日举办了知识竞答挑战赛.比赛共设置有A、B、C三关，每关设有若干问题，且每关的每个问题分值相同.参赛选手需回答完所有试题，答对得分，答错不扣分.甲、乙、丙三人作答完毕后，结果如下：甲在A、B、C三个关中回答正确的问题数目之比为 $2 ： 1 ： 1$ ，在A关的得分占甲总得分的75%；乙在A、B、C三个关中回答正确的问题数目之比为 $2 ： 5 ： 2$ ，在B关的得分占乙总得分的 $\frac{1}{3}$ ；丙在A关回答正确的问题数目是甲、乙在A关回答正确的问题数目之和的一半，丙在B关回答正确的问题数目比乙在B关回答正确的问题数目少 $\frac{2}{5}$ ，丙与甲在C关回答正确的数目相同，若甲、乙两人的总得分之比为 $48 ： 25$ ，则乙、丙两人的总得分之比为.

查看试题解析
23. “洞庭碧螺春，品香醉天下.”洞庭碧螺春产于苏州市太湖洞庭山，以形美、色艳、香浓、味醇“四绝”驰名中外.如图，若将一壶碧螺春茶倒满2个小杯，则还剩 $\frac{1}{4}$ 壶；若倒满1个小杯后再全部倒入1个大杯中，则只能倒满这个大杯的 $\frac{1}{2}$ .1个小杯与1个大杯的容积之比为.

查看试题解析
24. 利用两块完全相同的长方形木块测量一张桌子的高度，首先将木块按图一方式放置，再交换两木块的位置，按图二方式放置，测量数据如图，求桌子的高度.

查看试题解析

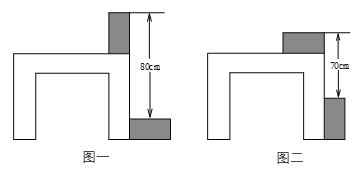
六、综合训练

25. 【方法体验】已知方程组 ${\begin{matrix} 2018 x - 2017 y = 20 ， ① \\ 2019 x + 2018 y = 500. ② \end{matrix}$ 求4037x＋y的值．小明同学发现解此方程组代入求值很麻烦!后来他将两个方程直接相加便迅速解决了问题．请你体验一下这种快捷思路，写出具体解题过程：
【方法迁移】根据上面的体验，填空：

已知方程组 ${\begin{array}{l} x + 2 y + 3 z = 10 \\ 4 x + 3 y + 2 z = 15 \end{array}$ 则3x＋y－z＝．

【探究升级】已知方程组 ${\begin{array}{l} x + 2 y + 3 z = 10 \\ 4 x + 3 y + 2 z = 15 \end{array}$ 求－2x＋y＋4z的值．小明凑出

“－2x＋y＋4z＝2•（x＋2y＋3z）＋（－1）•（4x＋3y＋2z）＝20－15＝5”，虽然问题获得解决，但他觉得凑数字很辛苦!他问数学老师丁老师有没有不用凑数字的方法，丁老师提示道：假设－2x＋y＋4z＝m•（x＋2y＋3z）＋n•（4x＋3y＋2z），对照方程两边各项的系数可列出方程组 ${\begin{matrix} m + 4 n = - 2 \\ 2 m + 3 n = 1 \\ 3 m + 2 n = 4 \end{matrix}$ ，它的解就是你凑的数!

根据丁老师的提示，填空：

2x＋5y＋8z＝（x＋2y＋3z）＋（4x＋3y＋2z）

【巩固运用】已知2a－b＋kc＝4，且a＋3b＋2c＝－2，当k为时，8a＋3b－2c为定值，此定值是．（直接写出结果）

查看试题解析
26. 若a、b、c、d为整数，且b是正整数，满足b+c＝d，c+d＝a，a+b=c，那么a+2b+3c+4d的最大值是．

查看试题解析
27. 明明和丽丽去书店买书，若已知明明买了A、B两本书共花费100.5元，丽丽买了A、C两本书共花费88.5元，则B书比C书贵元；若又知B、C两本书的总价钱恰好等于A书的价钱，则A、B、C三本书的总价钱为．

查看试题解析
28. 若实数 $x ， y ， z$ 满足 ${\begin{array}{l} x - y + 4 z = 1 \\ x - 2 y + 3 z = 3 \end{array}$ ，则 $x + y + 6 z =$ （）

A、 $- 3$ B、 $0$ C、 $3$ D、不能确定值

查看试题解析
29. 已知2x+y﹣z＝0，x+3y﹣2z＝0（xyz≠0），则x：y：z＝.

查看试题解析
30. 设 ${\begin{array}{l} 2 x + y + 3 z = 23 \\ x + 4 y + 5 z = 36 \end{array}$ ，则3x-2y+z= ．

查看试题解析
31. 若 $4 x - 3 y - 6 z = 0$ ， $x + 2 y - 7 z = 0 (x y z \neq 0)$ ，则代数式 $\frac{5 x^{2} + 2 y^{2} - z^{2}}{2 x^{2} - 3 y^{2} - 10 z^{2}}$ 的值是.

查看试题解析
32. 已知3x﹣y﹣2z＝0，2x+y﹣8z＝0，则 $\frac{x^{2} + y^{2} - z^{2}}{x y + y z}$ ＝.

查看试题解析
33. 已知 ${\begin{matrix} 4 x -3 y -6 z = 0, \\ 2 x + 4 y -14 z = 0 \end{matrix}$ (x,y,z≠0),则 $\frac{2 x^{2} + 3 y^{2} + 6 z^{2}}{x^{2} + 5 y^{2} + 7 z^{2}}$ 的值为.

查看试题解析
34. 一个三位数的各位数字的和等于18，百位数字与个位数字,的和比十位数字大14，如果把百位数字与个位数字对调，所得新数比原数大198，求原数!

查看试题解析
35. 一个三位数，个位，百位上的数字的和等于十位上的数字，百位上的数字的7倍比个位，十位上的数字的和大2，个位，十位，百位上的数字的和是14，求这个三位数.

查看试题解析
36. 甲、乙、丙三人共解100道数学题，每人都只会做其中的60道题，且三人合在一起，这100道都能解答出来，将其中只有一人会做的题目叫做难题，三人都会做的题叫容易题，则难题比容易题多（）

A、30道 B、25道 C、20道 D、15道

查看试题解析
37. 若购买甲商品3件，乙商品2件，丙商品1件，共需140元；购买甲商品1件，乙商品2件，丙商品3件，共需100元；那么购买甲商品1件，乙商品1件，丙商品1件，共需（）元．

A、50 B、60 C、70 D、80

查看试题解析
38. 已知三元一次方程组 ${\begin{array}{l} x + y = 3 \\ y + z = 4 \\ x + z = 5 \end{array}$ ，则 $x + y + z =$ .

查看试题解析