浙教版数学九年级知识点复习——二次函数、圆(含九下圆知识点)
试卷更新日期:2023-05-20 类型:期末考试
一、单选题
-
1. 二次函数的部分图象如图所示,图象过点 , 对称轴为直线 , 下列结论:
();();();()若点 , 点 , 点在该函数图象上,则;()若方程的两根为和 , 且 , 则 .
其中正确的结论有( )
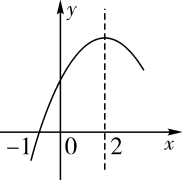 A、2个 B、3个 C、4个 D、5个2. 已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=-1,与x轴的一个交点B的坐标为(1,0)其图象如图所示,下列结论:①abc<0; ②2a-b=0; ③一元二次方程ax2+bx+c=0的两个根是-3和1;④当y>0时,-3<x<1;⑤当x>0时,y随x的增大而增大;⑥若点E(-4,y1),F(-2,y2),M(3,y3)是函数图象上的三点,则y1>y2>y3 , 其中正确的有( )个
A、2个 B、3个 C、4个 D、5个2. 已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=-1,与x轴的一个交点B的坐标为(1,0)其图象如图所示,下列结论:①abc<0; ②2a-b=0; ③一元二次方程ax2+bx+c=0的两个根是-3和1;④当y>0时,-3<x<1;⑤当x>0时,y随x的增大而增大;⑥若点E(-4,y1),F(-2,y2),M(3,y3)是函数图象上的三点,则y1>y2>y3 , 其中正确的有( )个 A、5 B、4 C、3 D、23. 二次函数(a,c为常数且)经过 , 且 , 下列结论:①;②;③若关于x的方程有整数解,则符合条件的p的值有3个;④当时,二次函数的最大值为c,则.其中一定正确的有( )A、1个 B、2个 C、3个 D、4个4. 如图是二次函数图象的一部分,图象过点 , 对称轴为直线 , ①②③当时,④若 , 为函数图象上的两点,则 , 以上结论中正确的有( )
A、5 B、4 C、3 D、23. 二次函数(a,c为常数且)经过 , 且 , 下列结论:①;②;③若关于x的方程有整数解,则符合条件的p的值有3个;④当时,二次函数的最大值为c,则.其中一定正确的有( )A、1个 B、2个 C、3个 D、4个4. 如图是二次函数图象的一部分,图象过点 , 对称轴为直线 , ①②③当时,④若 , 为函数图象上的两点,则 , 以上结论中正确的有( ) A、1个 B、2个 C、3个 D、4个5. 二次函数的部分图像如图,图像过点 , 对称轴为直线 , 下列结论:①;②;③;④;⑤当时,的值随值的增大而增大.其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个5. 二次函数的部分图像如图,图像过点 , 对称轴为直线 , 下列结论:①;②;③;④;⑤当时,的值随值的增大而增大.其中正确的结论有( ) A、2个 B、3个 C、4个 D、5个6. 如图,已知点C是线段AB的中点,CD⊥AB且CD=AB=a,延长CB至E,使得BE=b,以CD,CE为边作矩形CEFD,连接并延长DB,交FE的延长线于点G,连接AG,《几何原本》中利用该图解释了代数式(2a+b)2+b2=2[(a+b)2+a2]的几何意义,以AG为直径作圆,交AF于点H,若a=9,b=6,则HG的长为( )
A、2个 B、3个 C、4个 D、5个6. 如图,已知点C是线段AB的中点,CD⊥AB且CD=AB=a,延长CB至E,使得BE=b,以CD,CE为边作矩形CEFD,连接并延长DB,交FE的延长线于点G,连接AG,《几何原本》中利用该图解释了代数式(2a+b)2+b2=2[(a+b)2+a2]的几何意义,以AG为直径作圆,交AF于点H,若a=9,b=6,则HG的长为( ) A、5 B、18 C、3 D、177. 如图,点A、B分别在x轴、y轴上();以为直径的圆经过原点O,C是的中点,连结 , . 下列结论:①;②;③若 , , 则的面积等于5;④若 , 则点C的坐标是 , 其中正确的结论有( )
A、5 B、18 C、3 D、177. 如图,点A、B分别在x轴、y轴上();以为直径的圆经过原点O,C是的中点,连结 , . 下列结论:①;②;③若 , , 则的面积等于5;④若 , 则点C的坐标是 , 其中正确的结论有( ) A、4个 B、3个 C、2个 D、1个8. 如图,在给定的锐角三角形ABC中,∠BAC=60°,D是边BC上的一个动点,以AD为直径作⊙O分别交边AB,AC于点E,F,连接EF,当点D从点B运动到点C的过程中,线段EF的长度的大小变化情况是( )
A、4个 B、3个 C、2个 D、1个8. 如图,在给定的锐角三角形ABC中,∠BAC=60°,D是边BC上的一个动点,以AD为直径作⊙O分别交边AB,AC于点E,F,连接EF,当点D从点B运动到点C的过程中,线段EF的长度的大小变化情况是( )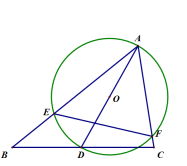 A、一直不变 B、一直减少 C、先减小后增大 D、先增大后减小9. 如图,四边形ABCD中,对角线AC,BD交于点E. 若 , 则下列结论中正确的是( )
A、一直不变 B、一直减少 C、先减小后增大 D、先增大后减小9. 如图,四边形ABCD中,对角线AC,BD交于点E. 若 , 则下列结论中正确的是( )
①
②与的周长比为③
④S△ABE·S△DCE=S△ADE·S△BCEA、③④ B、①②③ C、①②④ D、①②③④10. 如图,AC,BD是⊙O的两条直径,∠AOD=60°,点M是劣弧AB上任意一点,过点M作AC的垂线,交AC、BD所在直线于点E、G,过点M作BD的垂线,交BD、AC所在直线于点F、H,小明思考后提出如下说法,其中不正确的是( )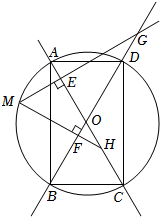 A、 B、∠EMF=60° C、当M平分弧AB时,四边形AMBO为菱形 D、当△MFG≌△BCD时,
A、 B、∠EMF=60° C、当M平分弧AB时,四边形AMBO为菱形 D、当△MFG≌△BCD时,二、填空题
-
11. 如图,抛物线与x轴正半轴交于两点,y轴负半轴交于点C.若点 , 则下列结论中: ;;与是抛物线上两点,若 , 则;若抛物线的对称轴是直线 , m为任意实数,则;若则其中正确结论的个数共有个.
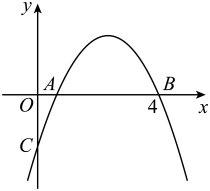 12. 已知过点的抛物线与坐标轴交于点、如图所示,连结 , , , 第一象限内有一动点在抛物线上运动,过点作交轴于点 , 当点在点上方,且与相似时,点的坐标为.
12. 已知过点的抛物线与坐标轴交于点、如图所示,连结 , , , 第一象限内有一动点在抛物线上运动,过点作交轴于点 , 当点在点上方,且与相似时,点的坐标为. 13. 如图,函数y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(-1,0),(m,0),且1<m<2,下列结论:①abc>0;②a+b<0;③若点A(-2,y1),B(2,y2)在抛物线上,则y1< y2;④
13. 如图,函数y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(-1,0),(m,0),且1<m<2,下列结论:①abc>0;②a+b<0;③若点A(-2,y1),B(2,y2)在抛物线上,则y1< y2;④若1≤c≤2,则a的取值范围是-2<a< . 其中结论正确的有 . (填序号)
 14. 已知,如图所示,矩形 , , , 是边上的一动点.连接 , 过作垂足为点,交于点.过A作 , 垂足为 , 连接.则四边形面积的最大值为.
14. 已知,如图所示,矩形 , , , 是边上的一动点.连接 , 过作垂足为点,交于点.过A作 , 垂足为 , 连接.则四边形面积的最大值为. 15. 已知关于的二次函数 , 其中为实数,当-2≤x≤1时,的最小值为4,满足条件的的值为。16. 如图,正五边形的对角线和分别交对角线于点 , , 若的面积为 , 则正五边形的面积为(结果用含的代数式表示).
15. 已知关于的二次函数 , 其中为实数,当-2≤x≤1时,的最小值为4,满足条件的的值为。16. 如图,正五边形的对角线和分别交对角线于点 , , 若的面积为 , 则正五边形的面积为(结果用含的代数式表示). 17. 在平面直角坐标系中,已知点 , 点 , 点 , 动点D从A点出发,以每秒1个单位的速度水平向右运动,动点E从点B出发,以每秒1个单位的速度竖直向上运动,过点A作交于点G,当线段的值最小时,则运动时间t的值为 .
17. 在平面直角坐标系中,已知点 , 点 , 点 , 动点D从A点出发,以每秒1个单位的速度水平向右运动,动点E从点B出发,以每秒1个单位的速度竖直向上运动,过点A作交于点G,当线段的值最小时,则运动时间t的值为 .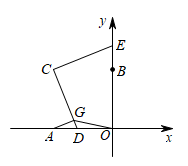 18. 定义:有一个圆分别和一个三角形的三条边各有两个交点,截得的三条弦相等,我们把这个圆叫作“等弦圆”,现在有一个斜边长为6的等腰直角三角形,当等弦圆最大时,这个圆的半径为 .
18. 定义:有一个圆分别和一个三角形的三条边各有两个交点,截得的三条弦相等,我们把这个圆叫作“等弦圆”,现在有一个斜边长为6的等腰直角三角形,当等弦圆最大时,这个圆的半径为 .三、解答题
-
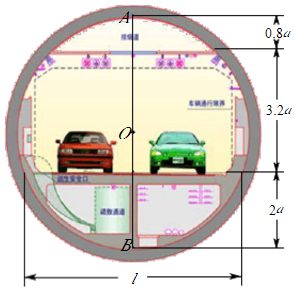
19. 生活中看似平常的隧道设计也很精巧.如图是一张盾构隧道断面结构图,隧道内部为以O为圆心AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为0.8a,顶棚到路面的距离是3.2a,点B到路面的距离为2a.请你求出路面的宽度l.(用含a的式子表示)
 20. 根据以下素材,探索完成任务.
20. 根据以下素材,探索完成任务.如何设计喷灌器喷水口的升降方案
素材1
随着自动化设备的普及,家庭庭院也引入自动喷灌系统.图1中某庭院内有一个可垂直升降的草坪喷灌器,从喷水口喷出的水柱成抛物线形.图2是该喷灌器OA喷水时的截面示意图,喷水口A点离地高度为0.25m,喷出的水柱在离喷水口水平距离为2m处达到最高,高度为0.45m,且水柱刚好落在庭院围墙和地面的交界B点处.

素材2
为了美化庭院,准备在庭院内沿围墙建花坛种植绣球花,花坛高0.4m,宽0.8m,侧面用大理石包围,长方形BCDE是花坛截面,如图3.调整喷水口的高度,喷出的水柱形状与原来相同,水柱落在花坛的上方DE边上(大理石厚度不计),达到给花坛喷灌的效果.

问题解决
任务1
确定水柱的形状
在图2中,建立合适的平面直角坐标系,求抛物线的表达式.
任务2
确定喷灌器的位置
求出喷灌器OA与围墙的距.
任务3
拟定喷头升降方案
调整喷水口的高度,使水柱可以喷灌花坛,求喷水口距离地面高度的最小值.
21. 如图,已知:关于y的二次函数 的图象与x轴交于点 和点B,与y轴交于点 ,抛物线的对称轴与x轴交于点D. (1)、求二次函数的表达式.(2)、在y轴上是否存在一点P,使 为直角三角形.若存在,请求出点P的坐标.(3)、有一个点M从点A出发,以每秒1个单位的速度在 上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达B点时,点M、N同时停止运动,问点M、N运动到何处时, 面积最大,试求出面积.22. 已知⊙O的直径为10,点A , 点B , 点C在⊙O上,∠CAB的平分线交⊙O于点D .
(1)、求二次函数的表达式.(2)、在y轴上是否存在一点P,使 为直角三角形.若存在,请求出点P的坐标.(3)、有一个点M从点A出发,以每秒1个单位的速度在 上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达B点时,点M、N同时停止运动,问点M、N运动到何处时, 面积最大,试求出面积.22. 已知⊙O的直径为10,点A , 点B , 点C在⊙O上,∠CAB的平分线交⊙O于点D .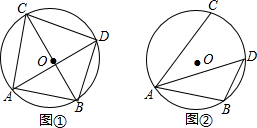
(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC , BD , CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
23. 如图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥,该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径是6cm,下底面直径为4cm,母线长为EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积(面积计算结果用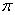 表示) .
表示) . 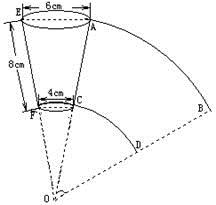 24. 如图,在Rt△ABC中,∠ACB=90°,AC=16,BC=12,点D、E分别为边AB、BC中点,点P从点A出发,沿射线AB方向以每秒5个单位长度的速度向点B运动,到点B停止.当点P不与点A重合时,过点P作PQ∥AC , 且点Q在直线AB左侧,AP=PQ , 过点Q作QM⊥AB交射线AB于点M . 设点P运动的时间为t(秒)
24. 如图,在Rt△ABC中,∠ACB=90°,AC=16,BC=12,点D、E分别为边AB、BC中点,点P从点A出发,沿射线AB方向以每秒5个单位长度的速度向点B运动,到点B停止.当点P不与点A重合时,过点P作PQ∥AC , 且点Q在直线AB左侧,AP=PQ , 过点Q作QM⊥AB交射线AB于点M . 设点P运动的时间为t(秒) (1)、用含t的代数式表示线段DM的长度;(2)、求当点Q落在BC边上时t的值;(3)、设△PQM与△DEB重叠部分图形的面积为S(平方单位),当△PQM与△DEB有重叠且重叠部分图形是三角形时,求S与t的函数关系式;(4)、当经过点C和△PQM中一个顶点的直线平分△PQM的内角时,直接写出此时t的值.
(1)、用含t的代数式表示线段DM的长度;(2)、求当点Q落在BC边上时t的值;(3)、设△PQM与△DEB重叠部分图形的面积为S(平方单位),当△PQM与△DEB有重叠且重叠部分图形是三角形时,求S与t的函数关系式;(4)、当经过点C和△PQM中一个顶点的直线平分△PQM的内角时,直接写出此时t的值.