2023年中考数学探究性试题复习19 相似
试卷更新日期:2023-05-20 类型:三轮冲刺
一、综合题
-
1. 已知点O是四边形ABCD内一点,AB=BC,OD=OC,∠ABC=∠DOC=α.
 (1)、如图1,α=60°,探究线段AD与OB的数量关系,并加以证明;(2)、如图2,α=120°,探究线段AD与OB的数量关系,并说明理由;(3)、结合上面的活动经验探究,请直接写出如图3中线段AD与OB的数量关系为(直接写出答案)2.(1)、【问题呈现】
(1)、如图1,α=60°,探究线段AD与OB的数量关系,并加以证明;(2)、如图2,α=120°,探究线段AD与OB的数量关系,并说明理由;(3)、结合上面的活动经验探究,请直接写出如图3中线段AD与OB的数量关系为(直接写出答案)2.(1)、【问题呈现】如图1,和都是等边三角形,连接 . 求证: .
 (2)、【类比探究】
(2)、【类比探究】如图2,和都是等腰直角三角形, . 连接 . 请直接写出的值.
(3)、【拓展提升】如图3,和都是直角三角形, , 且 . 连接 . 延长交于点F,交于点G.求的值.
3. 某校数学兴趣学习小组在一次活动中,对一些特殊几何图形具有的性质进行了如下探究: (1)、发现问题:如图1,在等腰中, , 点是边上任意一点,连接 , 以为腰作等腰 , 使 , , 连接 . 求证: .(2)、类比探究:如图2,在等腰中, , , , 点是边上任意一点,以为腰作等腰 , 使 , . 在点运动过程中,是否存在最小值?若存在,求出最小值,若不存在,请说明理由.(3)、拓展应用:如图3,在正方形中,点是边上一点,以为边作正方形 , 是正方形的中心,连接 . 若正方形的边长为 , , 求的面积.4.(1)、【探究发现】如图,在正方形中,E为边上一点,将沿BE翻折得到 , 延长交边于点G.求证:;
(1)、发现问题:如图1,在等腰中, , 点是边上任意一点,连接 , 以为腰作等腰 , 使 , , 连接 . 求证: .(2)、类比探究:如图2,在等腰中, , , , 点是边上任意一点,以为腰作等腰 , 使 , . 在点运动过程中,是否存在最小值?若存在,求出最小值,若不存在,请说明理由.(3)、拓展应用:如图3,在正方形中,点是边上一点,以为边作正方形 , 是正方形的中心,连接 . 若正方形的边长为 , , 求的面积.4.(1)、【探究发现】如图,在正方形中,E为边上一点,将沿BE翻折得到 , 延长交边于点G.求证:; (2)、【类比迁移】如图,在矩形中,E为边上一点,且 , 将沿翻折得到 , 延长交边于点G,延长交边于点H,且 , 求的长;
(2)、【类比迁移】如图,在矩形中,E为边上一点,且 , 将沿翻折得到 , 延长交边于点G,延长交边于点H,且 , 求的长; (3)、【实践创新】如图,为等腰三角形, , O为斜边的中点, M,N为线段上的动点,且满足 , 设 , , , 证明:.
(3)、【实践创新】如图,为等腰三角形, , O为斜边的中点, M,N为线段上的动点,且满足 , 设 , , , 证明:. 5.(1)、【操作发现】
5.(1)、【操作发现】如图1,点M是中边的中点.

请你用圆规和无刻度的直尺过点M作的平行线 , 交于点N;
(2)、在(1)的条件下,线段与的数量关系是;(3)、【类比探究】如图2,线段与射线有公共端点A,请你用圆规和无刻度的直尺在线段上作一个点N,使 .
 6. 【课本再现】黄金分割是一种最能引起美感的分割比例,具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值.我们知道:如图1,如果 , 那么称点为线段的黄金分割点.
6. 【课本再现】黄金分割是一种最能引起美感的分割比例,具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值.我们知道:如图1,如果 , 那么称点为线段的黄金分割点. (1)、【问题发现】如图1,请直接写出与的比值是;(2)、【尺规作黄金分割点】如图2,在中, , , , 则 , 在上截取 , 则 , 在上截取 , 则的值为;(3)、【问题解决】如图3,用边长为4的正方形纸片进行如下操作:对折正方形得折痕 , 连接 , 点对应点 , 得折痕 , 试说明:是的黄金分割点;(4)、【拓展延伸】如图4,正方形中,为对角线上一点,点在边上,且 , 当为的黄金分割点时, , 连 , 延长交于 , 请用相似的知识求出的值为 .7. 综合与实践:
(1)、【问题发现】如图1,请直接写出与的比值是;(2)、【尺规作黄金分割点】如图2,在中, , , , 则 , 在上截取 , 则 , 在上截取 , 则的值为;(3)、【问题解决】如图3,用边长为4的正方形纸片进行如下操作:对折正方形得折痕 , 连接 , 点对应点 , 得折痕 , 试说明:是的黄金分割点;(4)、【拓展延伸】如图4,正方形中,为对角线上一点,点在边上,且 , 当为的黄金分割点时, , 连 , 延长交于 , 请用相似的知识求出的值为 .7. 综合与实践:问题情境:如图1,在正方形中,点E是对角线上一点,连接 , 过点E分别作的垂线,分别交直线于点F,G.试猜想线段的数量关系并加以证明.
 (1)、数学思考:
(1)、数学思考:请解答上述问题;
(2)、问题解决:如图2,在图1的条件下,将“正方形”改为“矩形”,其他条件不变.若 , , 求的值;
(3)、问题拓展:在(2)的条件下,当点E为的中点时,请直接写出的面积.
8.(1)、课本再现如图1,在和中, , , ,
求证: . 我们在数学课上探索这一结论时进行了分析:要证 , 可设法证 , 若设 , 则只需证 .

请你根据以上分析,完成证明.
(2)、知识应用如图2,在四边形中, , , , 求的度数.
 9. B,C是⊙O上的两个定点,A是圆上的动点, , , .
9. B,C是⊙O上的两个定点,A是圆上的动点, , , . (1)、如图1,如果是等边三角形,求证是⊙O的切线;(2)、如图2,如果 , , 分别交⊙O于E,F,研究五边形的性质;
(1)、如图1,如果是等边三角形,求证是⊙O的切线;(2)、如图2,如果 , , 分别交⊙O于E,F,研究五边形的性质;①探索、和的数量关系,并证明你的结论;
②如图3,若⊙O的半径为6, , 求边的长;
③若 , , 直接写出 , 的数量关系.
10. 综合与探究问题情境:
数学活动课上,老师给出如下基础模型:如图①,已知 , , 过点C任作一条直线l(不与重合),过点A作于点D,过点B作于点E,当点A、B在直线l同侧时,易证(下列解题可直接用此结论).
 (1)、如图②,当点A、B在直线l异侧时,求证: .
(1)、如图②,当点A、B在直线l异侧时,求证: . (2)、模型应用:在平面直角坐标系中,已知直线l:(k为常数,)与x轴交于点A,与y轴的负半轴交于点B,以AB为边、B为直角顶点作直角三角形且 . 若直线l经过点 , 当点C在第三象限时,点C的坐标为 .(3)、若点D是函数图象上的点,且轴,当点C在第四象限时,连接交y轴于点E,求点C、D的坐标(用含k的式子表示)及的长.
(2)、模型应用:在平面直角坐标系中,已知直线l:(k为常数,)与x轴交于点A,与y轴的负半轴交于点B,以AB为边、B为直角顶点作直角三角形且 . 若直线l经过点 , 当点C在第三象限时,点C的坐标为 .(3)、若点D是函数图象上的点,且轴,当点C在第四象限时,连接交y轴于点E,求点C、D的坐标(用含k的式子表示)及的长. 11. 课本再现
11. 课本再现如图1,在等边中,为边上一点,为上一点,且 , 连接与相交于点 .
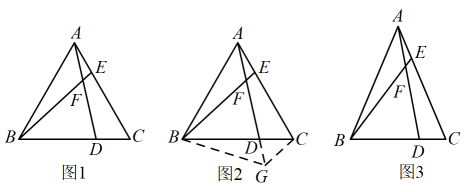 (1)、与的数量关系是 , 与构成的锐角夹角的度数是 .(2)、深入探究:将图1中的延长至点 , 使 , 连接 , , 如图2所示.求证:平分 . (第一问的结论,本问可直接使用)(3)、迁移应用:如图3,在等腰中, , , 分别是边 , 上的点,与相交于点 . 若 , 且 , 求的值.12. 矩形ABCD中,=(k>1),点E是边BC的中点,连接AE,过点E作AE的垂线EF,与矩形的外角平分线CF交于点F.
(1)、与的数量关系是 , 与构成的锐角夹角的度数是 .(2)、深入探究:将图1中的延长至点 , 使 , 连接 , , 如图2所示.求证:平分 . (第一问的结论,本问可直接使用)(3)、迁移应用:如图3,在等腰中, , , 分别是边 , 上的点,与相交于点 . 若 , 且 , 求的值.12. 矩形ABCD中,=(k>1),点E是边BC的中点,连接AE,过点E作AE的垂线EF,与矩形的外角平分线CF交于点F. (1)、【特例证明】如图(1),当k=2时,求证:AE=EF;
(1)、【特例证明】如图(1),当k=2时,求证:AE=EF;小明不完整的证明过程如下,请你帮他补充完整.
证明:如图,在BA上截取BH=BE,连接EH.
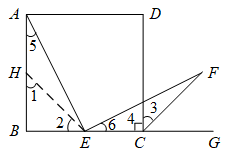
∵k=2,
∴AB=BC.
∵∠B=90°,BH=BE,
∴∠1=∠2=45°,
∴∠AHE=180°-∠1=135°.
∵CF平分∠DCG,∠DCG=90°,
∴∠3=∠DCG=45°.
∴∠ECF=∠3+∠4=135°.
∴……
(只需在答题卡对应区域写出剩余证明过程)
(2)、【类比探究】如图(2),当k≠2时,求的值(用含k的式子表示);(3)、【拓展运用】如图(3),当k=3时,P为边CD上一点,连接AP,PF,∠PAE=45°, , 求BC的长.13. 回顾:用数学的思维思考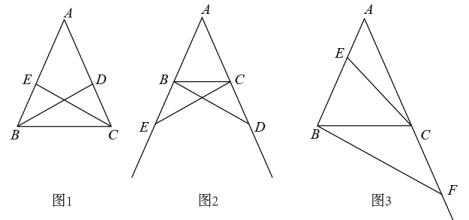 (1)、如图1,在△ABC中,AB=AC.
(1)、如图1,在△ABC中,AB=AC.①BD,CE是△ABC的角平分线.求证:BD=CE.
②点D,E分别是边AC,AB的中点,连接BD,CE.求证:BD=CE.
(从①②两题中选择一题加以证明)
(2)、猜想:用数学的眼光观察经过做题反思,小明同学认为:在△ABC中,AB=AC,D为边AC上一动点(不与点A,C重合).对于点D在边AC上的任意位置,在另一边AB上总能找到一个与其对应的点E,使得BD=CE.进而提出问题:若点D,E分别运动到边AC,AB的延长线上,BD与CE还相等吗?请解决下面的问题:
如图2,在△ABC中,AB=AC,点D,E分别在边AC,AB的延长线上,请添加一个条件(不再添加新的字母),使得BD=CE,并证明.
(3)、探究:用数学的语言表达如图3,在△ABC中,AB=AC=2,∠A=36°,E为边AB上任意一点(不与点A,B重合),F为边AC延长线上一点.判断BF与CE能否相等.若能,求CF的取值范围;若不能,说明理由.
14. 如图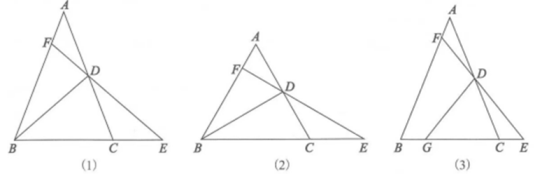
问题提出:如图(1),中, , 是的中点,延长至点 , 使 , 延长交于点 , 探究的值.
(1)、问题探究:
先将问题特殊化.如图(2),当时,直接写出的值;(2)、再探究一般情形.如图(1),证明(1)中的结论仍然成立.(3)、问题拓展:
如图(3),在中, , 是的中点,是边上一点, , 延长至点 , 使 , 延长交于点.直接写出的值(用含的式子表示).15. 如图 (1)、(问题发现)
(1)、(问题发现)
如图1,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B、C重合)将线段AD绕点A顺时针旋转90°得到AE,连结EC,则线段BD与CE的数量关系是 , 位置关系是;(2)、(探究证明)
如图2,在Rt△ABC和Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,当点C,D,E在同一直线时,BD与CE具有怎样的位置关系,并说明理由;(3)、(拓展延伸)
如图3,在Rt△BCD中,∠BCD=90°,BC=2CD=4,将△ACD绕顺时针旋转,点C对应点E,设旋转角∠CAE为α(0°<α<360°),当点C,D,E在同一直线时,画出图形,并求出线段BE的长度.