2023年中考数学探究性试题复习18 旋转

试卷更新日期：2023-05-20 类型：三轮冲刺

进入 出卷网 下载

一、综合题

  • 1.            
    (1)、综合与实践

    问题情境：如图1，在Rt△ABC中，AC=BC=2 ， ∠ACB=90° ， D，E分别是AC ， BC的中点，连接DE ．

    如图2，将△CDE绕着点C逆时针旋转a° ， 连接BE和AD ， 小明发现AD=BE ， BE⊥AD ， 请你证明该结论．

    (2)、猜想探究：

    如图3，将△CDE绕着点C逆时针旋转a°(0<α<90) ， 此时恰好有CE⊥BE ， 连接AD ， 延长BE ， 交AD于点F，试猜想四边形CDFE的形状，并说明理由．

    拓展探究：

    (3)、如图4，将△CDE绕着点C逆时针旋转a°(90<α<270) ， 直接写出四边形AEDB的面积的最大值．

    查看试题解析

  • 2. 在Rt△ABC和Rt△DEF中，∠C=∠F=90° ， ∠B=∠E=30° ， AC=AF=6 ， 用这两个直角三角形研究图形的变换.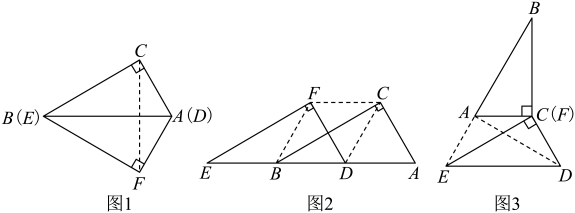

     

    (1)、【翻折】如图1，将△DEF沿线段AB翻折，连接CF ， 下列对所得四边形ACBF的说法正确的是.

    ①AB平分∠CBF、∠CAF ， ②AB、CF互相平分，③S四边形ACBF=12AB⋅CF ， ④A、C、B、F四点共圆.

    (2)、【平移】
    如图2，将△DEF沿线段AB向右平移，使D点移到AB的中点，连接CD、CF、FB ， 请猜想四边形CDBF的形状，并说明理由.
    (3)、【旋转】如图3，将△DEF绕点C(F)逆时针方向旋转，使AC∥ED ， 连接AE、AD ， 则旋转角为°，AD=cm.

    查看试题解析

  • 3. 在学习了图形的旋转知识后，数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究．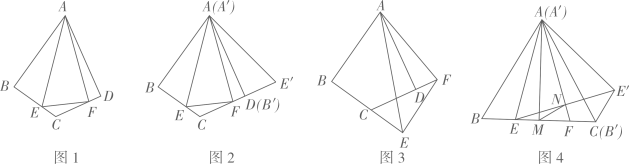

    （一）尝试探究：如图1，在四边形ABCD中，AB＝AD，∠BAD＝60°，∠ABC＝∠ADC＝90°，点E、F分别在线段BC、CD上，∠EAF＝30°，连接EF．

    (1)、如图2，将△ABE绕点A逆时针旋转60°后得到△A′B′E′（A′B′与AD重合），请直接写出∠E′AF＝度，线段BE、EF、FD之间的数量关系为 ．
    (2)、如图3，当但点E、F分别在线段BC、CD的延长线上时，其他条件不变，请探究线段BE、EF、FD之间的数量关系，并说明理由．
    (3)、拓展延伸：如图4，在等边△ABC中，E、F是边BC上的两点，∠EAF＝30°，BE＝1，将△ABE绕点A逆时针旋转60°得到△A′B′E′（A′B′与AC重合），连接EE′，AF与EE′交于点N，过点A作AM⊥BC于点M，连接MN，求线段MN的长度．

    查看试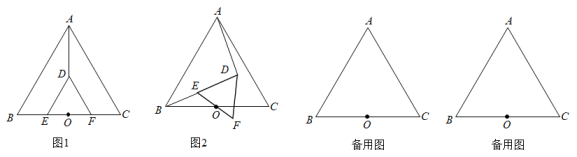题解析

  • 4. 如图

    (1)、问题发现：

    如图1，△ABC和△DEF都是等边三角形，边BC和EF在同一直线上，O是边BC的中点，BE=CF ， 连接AD ， 则下列结论正确的是 ． （填序号即可）

    ①OE=OF；②AD=BE；③AD⊥BE；④整个图形是轴对称图形．

    (2)、数学思考：将图1中的△DEF绕着点O旋转，△ABC不动，连接AD和BE ， 如图2，则AD和BE具有怎样的数量和位置关系？请给出证明过程；
    (3)、拓展应用：已知AB=8cm ， DE=4cm ， 在图1中的△DEF绕着点O旋转的过程中，当BE⊥DF时，求线段AD的长度．

    查看试题解析

  • 5. 在正方形ABCD中，点E是对角线AC上的动点（与点A ， C不重合），连接BE ．

    (1)、将射线BE绕点B顺时针旋转45° ， 交直线AC于点F ．

    ①依题意补全图1；

    ②小深通过观察、实验，发现线段AE ， FC ， EF存在以下数量关系：AE与FC的平方和等于EF的平方．小深把这个猜想与同学们进行交流，通过讨论，形成证明该猜想的几种想法：

    想法1：将线段BF绕点B逆时针旋转90° ， 得到线段BM ， 要证AE ， FC ， EF的关系，只需证AE ， AM ， EM的关系．

    想法2：将△ABE沿BE翻折，得到△NBE ， 要证AE ， FC ， EF的关系，只需证EN ， FN ， EF的关系．

    …

    请你参考上面的想法，用等式表示线段AE ， FC ， EF的数量关系并证明；（一种方法即可）

    (2)、如图2，若将直线BE绕点B顺时针旋转135° ， 交直线AC于点F ． 若正方形边长为2 ， AE：EC=2：3 ， 求AF的长．

    查看试题解析

  • 6.     
    (1)、【问题初探】

    如图1，等腰Rt△ABC中，AB=AC ， 点D为AB边一点，以BD为腰向下作等腰Rt△BDE ， ∠DBE=90° ． 连接CD ， CE ， 点F为CD的中点，连接AF ． 猜想并证明线段AF与CE的数量关系和位置关系．

    (2)、【深入探究】

    在（1）的条件下 ， 如图2，将等腰Rt△BDE绕点B旋转，上述结论是否仍然成立？若成立，请证明；若不成立，请说明理由．

    (3)、【拓展迁移】

    如图3，等腰△ABC中，AB=AC ， ∠BAC=120° ． 在Rt△BDE中，∠DBE=90° ， ∠BDE=12∠BAC ． 连接CD ， CE ， 点F为CD的中点，连接AF ．

    Rt△BDE绕点B旋转过程中，

    ①线段AF与CE的数量关系为：；

    ②若BC=413 ， BD=23 ， 当点F在等腰△ABC内部且∠BCF的度数最大时，线段AF的长度为 ．

    查看试题解析

  • 7. 如图1，在Rt△ABC中，∠A=90° ， AB=AC ， 点D、E分别在边AB，AC上，AD=AE ， 连接DC，点M，P，N分别为DE，DC，BC的中点.

    (1)、观察猜想：图中，线段PM与PN的数量关系是 ， 位置关系是；
    (2)、探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，连接MN ， BD ， CE ， 判断△PMN的形状，并说明理由；

    (3)、拓展延伸：把△ADE绕点A在平面内自由旋转，若AD=4 ， AB=10 ， 请直接写出△PMN面积的最大值.

    查看试题解析

  • 8. 如图1，在Rt△ABC中，∠BAC＝90° ， AB＝AC ， D，E两点分别在AB ， AC上，且DE∥BC ， 将△ADE绕点A顺时针旋转，记旋转角为α ．

    (1)、问题发现 当α＝0°时，线段BD ， CE的数量关系是；
    (2)、拓展探究 当0°≤α＜360°时，（1）中的结论有无变化？请仅就图2的情形给出证明；
    (3)、问题解决 设DE＝2 ， BC＝6 ， 0°≤α＜360° ， △ADE旋转至A，B，E三点共线时，直接写出线段BE的长．

    查看试题解析

  • 9. 如图1，点O在直线AB上，过点O引一条射线OC ， 使∠AOC=50° ， 将一个直角三角尺的直角顶点放在点O处，直角边OM在射线OB上，另一边ON在直线AB的下方.

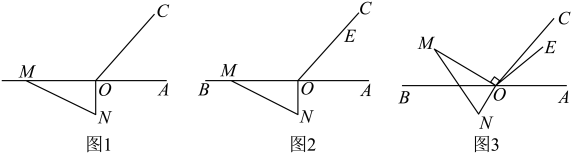
    【操作一】：将图1中的三角尺绕着点O以每秒15°的速度按顺时针方向旋转.当它完成旋转一周时停止，设旋转的时间为t秒.

    (1)、∠BOC的度数是 ， 图1中与它互补的角是.
    (2)、三角尺旋转的度数可表示为（用含t的代数式表示）；当t=时，MO⊥OC.
    (3)、【操作二】：如图2将一把直尺的一端点也放在点O处，另一端点E在射线OC上.如图3，在三角尺绕着点O以每秒15°的速度按顺时针方向旋转的同时，直尺也绕着点O以每秒5°的速度按顺时针方向旋转，当一方完成旋转一周时停止，另一方也停止旋转，设旋转的时间为t秒.

    试探索：在三角尺与直尺旋转的过程中，当0≤t≤623 ， 是否存在某个时刻，使得∠COM与∠COE中其中一个角是另一个角的两倍？若存在，请求出所有满足题意的t的值；若不存在，请说明理由.

    查看试题解析

  • 10. 阅读下面材料.

    小炎遇到这个一个问题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45° ， 连接EF ， 则EF=BE+DF ， 试说明理由.

    小炎是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段相对集中，她先尝试了翻折、旋转、平移的方法，最后发现线段AB、AD是共点并且相等的，于是找到解决问题的方法.她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG ， 再利用全等的知识解决这个问题（如图2）.

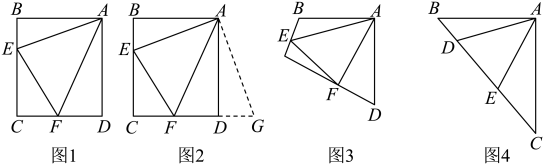
    参考小炎同学思考问题的方法，解决下列问题：

    (1)、写出小炎的推理过程；
    (2)、如图3，四边形ABCD中，AB=AD ， ∠BAD=90° ， 点E、F分别在边BC、CD上，∠EAF=45° ， 若∠B、∠D都不是直角，则当∠B与∠D满足于关系时，仍有EF=BE+DF；
    (3)、如图4，在△ABC中，∠BAC=90° ， AB=AC ， 点D、E均在边BC上，且∠DAE=45° ， 若BD=1 ， EC=2 ， 求DE的长.

    查看试题解析

  • 11. 请阅读下列材料：已知：如图（1）在Rt△ABC中，∠BAC=90° ， AB=AC ， 点D、E分别为线段BC上两动点，若∠DAE=45°.探究线段BD、DE、EC三条线段之间的数量关系.小明的思路是：把△AEC绕点A顺时针旋转90° ， 得到△ABE' ， 连接E'D ， 使问题得到解决.请你参考小明的思路探究并解决下列问题：

    (1)、猜想BD、DE、EC三条线段之间存在的数量关系式，直接写出你的猜想；
    (2)、当动点E在线段BC上，动点D运动在线段CB延长线上时，如图（2），其它条件不变，（1）中探究的结论是否发生改变？请说明你的猜想并给予证明；
    (3)、已知：如图（3），等边三角形ABC中，点D、E在边AB上，且∠DCE=30° ， 请你找出一个条件，使线段DE、AD、EB能构成一个等腰三角形，并求出此时等腰三角形顶角的度数.

    查看试题解析

  • 12. 如图，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90° ， ∠B=∠E=30° ．

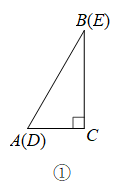
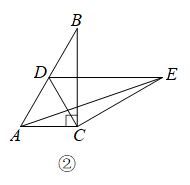
    (1)、操作发现

    如图②，固定△ABC ， 使△DEC绕点C旋转，当点D恰好落在AB边上时，

    ①求线段DE与AC的位置关系；

    ②设△BDC的面积为S1 ， △AEC的面积为S2 ， 求S1与S2的数量关系．

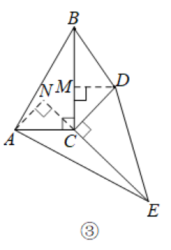
    (2)、猜想论证

    当△DEC绕点C旋转到如图③所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想．

    查看试题解析

  • 13. 综合与实践

    问题情境：

    将两个完全相同的等腰Rt△ABC和等腰Rt△CDE按图1方式放置，∠ACB=∠DCE=90°，将Rt△CDE绕点C顺时针旋转，连接AE，BD，AE与BD相交于点G．

    猜想证明：

    (1)、在图1中，请判断AE与BD的数量关系与位置关系，并说明理由；

    (2)、当旋转到CE//AB时，如图2，证明：AE平分∠BAC；

    (3)、若旋转到如图3所示的位置时，连接BE、此时△BCE恰好是等边三角形，AE与BC相交于点F，请你直接写出BFCF的值．

    查看试题解析

  • 14. 含有45°的直角三角板ABC和含有30°的直角三角板BDE按如图1放置，AB和BE重合.

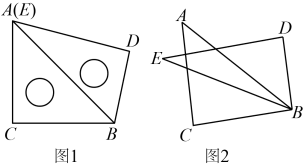
    【操作一】三角板ABC保持不变，将三角板BDE绕着点B以每秒15°的速度按逆时针方向旋转.当它完成旋转一周时停止，设旋转的时间为t秒.

    (1)、当t=0时，∠CBD=度.
    (2)、求t为何值时，BD⊥BC.

    【操作二】如图2，在三角板BDE绕着点B以每秒15°的速度按逆时针方向旋转的同时，三角板ABC也绕着点B以每秒5°的速度按逆时针方向旋转，设旋转时间为t秒（0<t≤18）.

    (3)、求t为何值时，BD与AB重合.
    (4)、试探索：在两个三角板旋转的过程中，是否存在某个时刻，使得∠ABD与∠ABE中其中一个角是另一个角的两倍？若存在，请求出所有满足题意的t的值；若不存在，请说明理由.

    查看试题解析

  • 15. 通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的.下面是一个案例，请补充完整.

    原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由.

    (1)、思路梳理

    ∵AB=CD，

    ∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合.

    ∵∠ADC=∠B=90°，

    ∴∠FDG=180°，点F、D、G共线.

    根据 ， 易证△AFG≌ ， 得EF=BE+DF.

    (2)、类比引申

    如图2，四边形ABCD中，AB=AD，∠BAD=90°，点E、F分别在边BC、CD上，∠EAF=45°.若∠B、∠D都不是直角，则当∠B与∠D满足等量关系时，仍有EF=BE+DF.

    (3)、联想拓展

    如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°.猜想BD、DE、EC应满足的等量关系，并写出推理过程.

    查看试题解析

  • 16. 某校一数学兴趣小组在一次合作探究活动中，将两块大小不同的等腰直角三角形 ABC 和等腰直角三角形 CDE ，按如图1的方式摆放， ∠ACB=∠ECD=90° ，随后保持 △ABC 不动，将 △CDE 绕点C按逆时针方向旋转 α （ 0°<α<90° ），连接 AE ， BD ，延长 BD 交 AE 于点F，连接 CF .该数学兴趣小组进行如下探究，请你帮忙解答：

    【初步探究】

    (1)、如图2，当 ED∥BC 时，则 α= ；
    (2)、如图3，当点E，F重合时，请直接写出 AF ， BF ， CF 之间的数量关系：；
    (3)、如图4，当点E，F不重合时，（2）中的结论是否仍然成立？若成立，请给出推理过程；若不成立，请说明理由.
    (4)、如图5，在 △ABC 与 △CDE 中， ∠ACB=∠DCE=90° ，若 BC=mAC ， CD=mCE （m为常数）.保持 △ABC 不动，将 △CDE 绕点C按逆时针方向旋转 α （ 0°<α<90° ），连接 AE ， BD ，延长 BD 交 AE 于点F，连接 CF ，如图6.试探究 AF ， BF ， CF 之间的数量关系，并说明理由.

    查看试题解析

  • 17. 如图

     

    (1)、（问题发现）
    如图1，在Rt△ABC中，AB＝AC，D为BC边上一点（不与点B、C重合）将线段AD绕点A顺时针旋转90°得到AE，连结EC，则线段BD与CE的数量关系是 ， 位置关系是；
    (2)、（探究证明）
    如图2，在Rt△ABC和Rt△ADE中，AB＝AC，AD＝AE，将△ADE绕点A旋转，当点C，D，E在同一直线时，BD与CE具有怎样的位置关系，并说明理由；
    (3)、（拓展延伸）
    如图3，在Rt△BCD中，∠BCD＝90°，BC＝2CD＝4，将△ACD绕顺时针旋转，点C对应点E，设旋转角∠CAE为α（0°＜α＜360°），当点C，D，E在同一直线时，画出图形，并求出线段BE的长度．

    查看试题解析