2023年中考数学探究性试题复习17 轴对称

试卷更新日期：2023-05-20 类型：三轮冲刺

进入出卷网下载

一、综合题

1. 如图

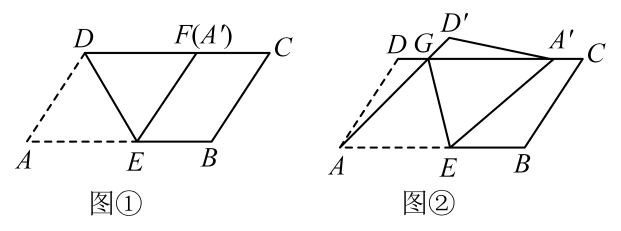(1)、【感知】如图①，将 $▱ A B C D$ 沿过点D的直线折叠，使点A落在 $C D$ 边上的点F处，得到折痕 $D E$ ，连结 $E F$ ．若 $A D = 4$ ，则四边形 $A E F D$ 的周长为．

(2)、【探究】如图②，将四边形 $A E G D$ 沿GE折叠，点A、D的对应点分别为 $A^{'}$ 、 $D^{'}$ ，点 $A^{'}$ 恰好落在 $C D$ 边上．
求证：四边形 $A E A^{'} G$ 为菱形．

(3)、若 $A B = 6$ ， $C B = 3$ ， $∠ B = 120 °$ ， $C A^{'} = 1$ ，则 $△ A^{'} G D^{'}$ 的面积为．

查看试题解析
2. 综合与探究
在矩形 $A B C D$ 的 $C D$ 边上取一点 $E$ ，将 $△ B C E$ 沿 $B E$ 翻折，使点 $C$ 恰好落在 $A D$ 边上的点 $F$ 处．

(1)、如图①，若 $B C = 2 B A$ ，求 $∠ C B E$ 的度数；

(2)、如图②，当 $A B = 5$ ，且 $A F \cdot F D = 10$ 时，求 $E F$ 的长；

(3)、如图③，延长 $E F$ ，与 $∠ A B F$ 的角平分线交于点 $M$ ， $B M$ 交 $A D$ 于点 $N$ ，当 $N F = A N + F D$ 时，请直接写出 $\frac{A B}{B C}$ 的值．

查看试题解析
3. 在 $R t △ A B C$ 和 $R t △ D E F$ 中， $∠ C = ∠ F = 90 °$ ， $∠ B = ∠ E = 30 °$ ， $A C = A F = 6$ ，用这两个直角三角形研究图形的变换.

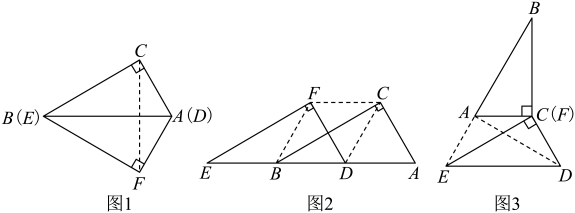(1)、【翻折】如图1，将 $△ D E F$ 沿线段 $A B$ 翻折，连接 $C F$ ，下列对所得四边形 $A C B F$ 的说法正确的是.
① $A B$ 平分 $∠ C B F$ 、 $∠ C A F$ ， ② $A B$ 、 $C F$ 互相平分，③ $S_{四边形 A C B F} = \frac{1}{2} A B \cdot C F$ ， ④ $A$ 、 $C$ 、 $B$ 、 $F$ 四点共圆.

(2)、【平移】
如图2，将 $△ D E F$ 沿线段 $A B$ 向右平移，使 $D$ 点移到 $A B$ 的中点，连接 $C D$ 、 $C F$ 、 $F B$ ，请猜想四边形 $C D B F$ 的形状，并说明理由.

(3)、【旋转】如图3，将 $△ D E F$ 绕点 $C (F)$ 逆时针方向旋转，使 $A C ∥ E D$ ，连接 $A E$ 、 $A D$ ，则旋转角为°， $A D =$ cm.

查看试题解析
4. 如图

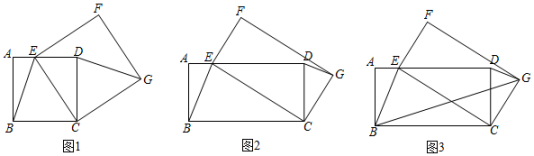(1)、【问题情境】如图1，四边形ABCD是正方形，点E是AD边上的一个动点，以CE为边在CE的右侧作正方形CEFG，连接DG、BE，则DG与BE的数量关系是；

(2)、如图2，四边形ABCD是矩形，AB=2，BC=4，点E是AD边上的一个动点，以CE为边在CE的右侧作矩形CEFG，且CG：CE=1：2，连接DG、BE.判断线段DG与BE有怎样的数量关系和位置关系，并说明理由；

(3)、【拓展提升】如图3，在（2）的条件下，连接BG，则2BG+BE的最小值为.

查看试题解析
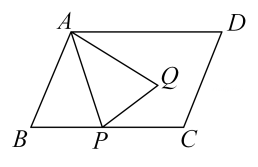
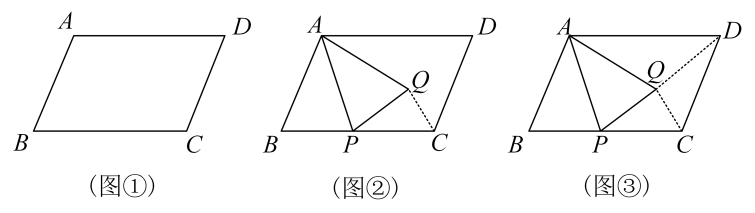5. 如图，平行四边形 $A B C D$ 中， $A B = 7$ ， $B C = 10 .$ 点 $P$ 是 $B C$ 边上的一点，连接 $A P$ ，以 $A P$ 为对称轴作 $△ A B P$ 的轴对称图形 $△ A Q P$ .

(1)、动手操作
当点 $Q$ 正好落在 $A D$ 边上时，在图①中画出 $△ A B P$ 的轴对称图形 $△ A Q P$ ，并判断四边形 $A B P Q$ 的形状是 ▲ ；

(2)、问题解决
如图②，当点 $P$ 是线段 $B C$ 中点，且 $C Q = 2$ 时，求 $A P$ 的长；

(3)、拓展探究
如图③，当点 $P$ 、 $Q$ 、 $D$ 在同一直线上，且 $∠ P Q C = ∠ P Q A$ 时，求 $P Q$ 的长.

查看试题解析
6. 在一个数学活动中，若身旁没有量角器或者三角尺，又需要作 $60 °$ ， $30 °$ ， $15 °$ 的角，可以采用如下的方法：
【操作感知】

第一步：对折矩形纸片 $A B C D$ ，使 $A D$ 与 $B C$ 重合，得到折痕 $E F$ ，把纸片展开.

第二步；再一次折叠纸片，使点 $A$ 落在 $E F$ 上，并使折痕经过点 $B$ ，得到折痕 $B M$ ，同时得到线段 $B N$ （如图1）.

(1)、【猜想论证】
写出图1中一个 $30 °$ 的角：.

(2)、若延长 $M N$ 交 $B C$ 于点 $P$ ，如图 $2$ 所示，试判断 $△ B M P$ 的形状，并证明.

(3)、【迁移探究】
小华将矩形纸片换正方形纸片，继续探究，过程如下：
将正方形纸片 $A B C D$ 按照 $“$ 操作感知 $”$ 的方式操作，并延长 $M N$ 交 $C D$ 于点 $Q$ ，连接 $B Q$ .当点 $N$ 在 $E F$ 上时， $D M = 2$ ，求正方形的边长.

查看试题解析
7.

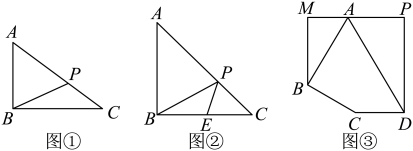(1)、问题提出
如图①，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $A B = 5$ ， $B C = 12$ ，若P是边 $A C$ 上一点，则 $B P$ 的最小值为.

(2)、问题探究
如图②，在 $R t △ A B C$ 中， $A B = B C$ ，斜边 $A C$ 的长为 $4 \sqrt{2}$ ， E是 $B C$ 的中点，P是边 $A C$ 上一点，试求 $P B + P E$ 的最小值.

(3)、问题解决
某城区有一个五边形 $M B C D P$ 空地（ $∠ M = ∠ P = ∠ P D C = 90 °$ ， $∠ C = 150 °$ ），城建部门计划利用该空地建造一个居民户外活动广场，其中 $△ M A B$ 的部分规划为观赏区，用于种植各类鲜花， $△ A P D$ 部分规划为音乐区，供老年合唱团排练合唱或广场舞使用，四边形 $A B C D$ 部分为市民健身广场，如图③所示.已知 $A D = 100$ 米， $C D = 50$ 米， $∠ B A D = 60 °$ ， $∠ A B C = 90 °$ .为了进一步提升服务休闲功能，满足市民游园和健身需求，现要在 $A B$ ， $A D$ 上分别取点E，F，铺设一条由 $C E$ ， $E F$ ， $F C$ 连接而成的步行景观道，已知铺设景观道的成本为100元/米，求铺设完这条步行景观道所需的最低成本.

查看试题解析
8. 综合与实践课上，老师让同学们以“正方形的折叠”为主题开展数学活动．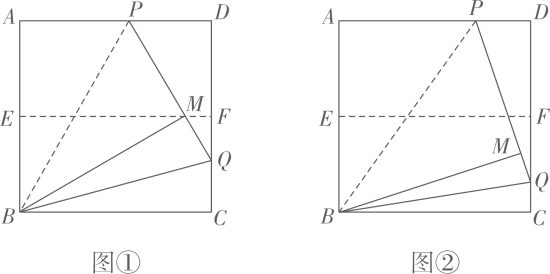

操作：

操作一：对折正方形纸片 $A B C D$ ，使 $A D$ 与 $B C$ 重合，得到折痕 $E F$ ，把纸片展平；

操作二：在 $A D$ 上选一点P，沿 $B P$ 折叠，使点A落在正方形内部点M处，把纸片展平，连接 $P M 、 B M$ ，延长 $P M$ 交 $C D$ 于点Q，连接 $B Q$ ．

(1)、探究：
①如图①，当点M在 $E F$ 上时， $∠ E M B =$ ▲ $°$ ．
②改变点P在 $A D$ 上的位置（点P不与点A、D重合），如图②，判断 $M Q$ 与 $C Q$ 的数量关系，并说明理由．

(2)、拓展：若正方形纸片 $A B C D$ 的边长为8，当 $F Q = 1$ 时，直接写出 $A P$ 的长．

查看试题解析
9. 将纸片△ABC沿DE折叠使点A落在点A'处.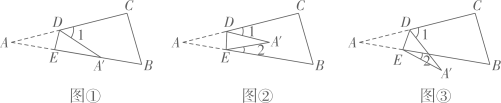
【感知】如图①，点A落在四边形BCDE的边BE上，则∠A与∠1之间的数量关系是 ▲ ；
【探究】如图②，若点A落在四边形BCDE的内部，则∠A与∠1+∠2之间存在怎样的数量关系？并说明理由.
【拓展】如图③，点A落在四边形BCDE的外部，若∠1=80°，∠2=24°，则∠A的大小为 ▲ .

查看试题解析
10. 问题情境：
数学活动课上，同学们开展了以“矩形纸片折叠”为主题的探究活动（每个小组的矩形纸片规格相同），已知矩形纸片宽AB＝8，长AD＝8 $\sqrt{2}$ .
动手实践：

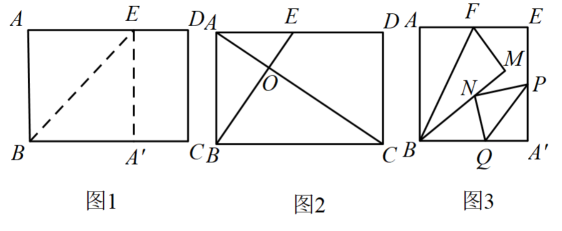(1)、如图1，腾飞小组将矩形纸片ABCD折叠，点A落在BC边上的点 $A^{'}$ 处，折痕为BE，连接 $A^{'} E$ ，然后将纸片展平，得到四边形 $A E A^{'} B$ ，则折痕BE的长为.

(2)、如图2，永攀小组将矩形纸片ABCD沿经过A、C两点的直线折叠，展开后得折痕AC.再将其沿经过点B的直线折叠，使点A落在OC上（O为两条折痕的交点），第二条折痕与AD交于点E.请写出OC与OA的数量关系，并说明理由.

(3)、如图3，探究小组将图1中的四边形 $A E A^{'} B$ 剪下，在AE上取中点F，将△ABF沿BF折叠得到△MBF，点P、Q分别是边 $A^{'} E ， A^{'} B$ 上的动点（均不与顶点重合），将 $△ A^{'} P Q$ 沿PQ折叠使 $A^{'}$ 的对应点N恰好落在BM上，当 $△ A^{'} P Q$ 的一个内角与 $∠ A^{'} B M$ 相等时，请直接写出 $A^{'} Q$ 的长.

查看试题解析
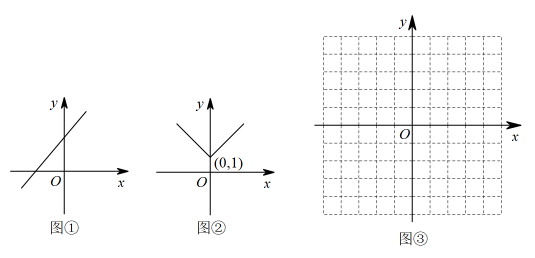11. 定义：在平面直角坐标系中，有一条直线 $x = m$ ，对于任意一个函数，作该函数自变量大于 $m$ 的部分关于直线 $x = m$ 的轴对称图形，与原函数中自变量大于或等于 $m$ 的部分共同构成一个新的函数图象，则这个新函数叫做原函数关于直线 $x = m$ 的“镜面函数”.例如：图① 是函数 $y = x + 1$ 的图象，则它关于直线 $x = 0$ 的“镜面函数”的图象如图② 所示，且它的“镜面函数”的解析式为 $y = {\begin{array}{l} x + 1 (x \geq 0) \\ - x + 1 (x < 0) \end{array}$ ，也可以写成 $y = | x | + 1$ .

(1)、在图③ 中画出函数 $y = - 2 x + 1$ 关于直线 $x = 1$ 的“镜面函数”的图象.

(2)、函数 $y = x^{2} - 2 x + 2$ 关于直线 $x = - 1$ 的“镜面函数”与直线 $y = - x + m$ 有三个公共点，求 $m$ 的值.

(3)、已知 $A (- 1 ， 0)$ ， $B (3 ， 0)$ ， $C (3 ， - 2)$ ， $D (- 1 ， - 2)$ ，函数 $y = x^{2} - 2 n x + 2 (n > 0)$ 关于直线 $x = 0$ 的“镜面函数”图象与矩形 $A B C D$ 的边恰好有4个交点，求n的取值范围.

查看试题解析
12. 在平面直角坐标系 $x O y$ 中，对于线段AB与直线 $l ： y = k x + b$ ，给出如下定义：若线段AB关于直线l的对称线段为 $A^{'} B^{'}$ ( $A^{'}$ ， $B^{'}$ 分别为点A，B的对应点)，则称线段 $A^{'} B^{'}$ 为线段AB的“ $[k ， b]$ 关联线段”．
已知点 $A (1 ， 1)$ ， $B (1 ， - 1)$ ．

(1)、线段 $A^{'} B^{'}$ 为线段AB的“ $[1 ， b]$ 关联线段”，点 $A^{'}$ 的坐标为 $(2 ， 0)$ ，则 $A^{'} B^{'}$ 的长为， b的值为；

(2)、线段 $A^{'} B^{'}$ 为线段AB的“ $[k ， 0]$ 关联线段”，直线 $l_{1}$ 经过点 $C (0 ， 2)$ ，若点 $A^{'}$ ， $B^{'}$ 都在直线 $l_{1}$ 上，连接 $O A^{^{'}}$ ，求 $∠ C O A^{'}$ 的度数；

(3)、点 $P (- 3 ， 0)$ ， $Q (- 3 ， 3)$ ，线段 $A^{'} B^{'}$ 为线段AB的“ $[k ， b]$ 关联线段”，且当b取某个值时，一定存在k使得线段 $A^{'} B^{'}$ 与线段PQ有公共点，直接写出b的取值范围．

查看试题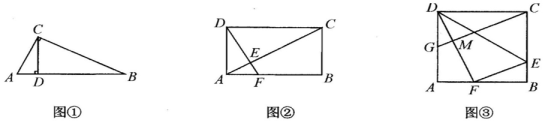解析
13. 如图

(1)、[基础巩固]如图①，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，求证：AC²=AD·AB．

(2)、[尝试应用] 如图②，在矩形ABCD中，AD=2，点F在AB上，FB=2AF，DF⊥AC于点E，求AE的长．

(3)、[拓展提高] 如图③，在矩形ABCD中，点E在边BC上，NDCE与NDFE关于直线DE对称，点C的对称点F在边AB上，G为AD中点，连结GC交DF于点M，GC∥FE，若AD=2，求GM的长．

查看试题解析
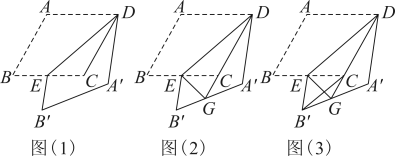14. 在数学兴趣小组活动中，同学们对菱形的折叠问题进行了探究.如图（1），在菱形 $A B C D$ 中， $∠ B$ 为锐角， $E$ 为 $B C$ 中点，连接 $D E$ ，将菱形 $A B C D$ 沿 $D E$ 折叠，得到四边形 $A^{'} B^{'} E D$ ，点 $A$ 的对应点为点 $A ′$ ，点 $B$ 的对应点为点 $B ′$ .

(1)、【观察发现】 $A^{'} D$ 与 $B^{'} E$ 的位置关系是；

(2)、【思考表达】连接 $B^{'} C$ ，判断 $∠ D E C$ 与 $∠ B^{'} C E$ 是否相等，并说明理由；

(3)、如图（2），延长 $D C$ 交 $A^{'} B^{'}$ 于点 $G$ ，连接 $E G$ ，请探究 $∠ D E G$ 的度数，并说明理由；

(4)、【综合运用】如图（3），当 $∠ B = 60 °$ 时，连接 $B^{'} C$ ，延长 $D C$ 交 $A^{'} B^{'}$ 于点 $G$ ，连接 $E G$ ，请写出 $B^{'} C$ 、 $E G$ 、 $D G$ 之间的数量关系，并说明理由.

查看试题解析