2023年中考数学探究性试题复习16 圆

试卷更新日期：2023-05-20 类型：三轮冲刺

进入出卷网下载

一、综合题

1.

(1)、【教材呈现】以下是浙教版八年级下册数学教材第85页的部分内容．先观察图4－17，直线l1∥l2，点A，B在直线l₂上，点C₁ ， C₂ ， C₃ ， C₄在直线l₁上．△ABC₁ ， △ABC₂ ， △ABC₃ ， △ABC₄这些三角形的面积有怎样的关系？请说明理由。

(2)、【基础巩固】如图1，正方形ABCD内接于⊙O，直径MN∥AD，求阴影面积与圆面积的比值；

(3)、【尝试应用】如图2，在半径为5的⊙O中，BD＝CD，∠ACO＝2∠BDO，cos∠BOC＝x，用含x的代数式表示S△ABC；

(4)、【拓展提高】如图3，AB是⊙O的直径，点P是OB上一点，过点P作弦CD⊥AB于点P，点F是⊙O上的点，且满足CF＝CB，连接BF交CD于点E，若BF＝8EP，S△CEF=10 $\sqrt{2}$ ，求⊙O的半径．

查看试题解析
2. “同弧或等弧所对的圆周角相等”，利用这个推论可以解决很多数学问题.

(1)、【知识理解】如图10，圆О的内接四边形ACBD中， $∠ A B C = 60 °$ ， $B C = A C$ ，
① $∠ B D C =$ ； $∠ D A B$ $∠ D C B$ （填“>”，“=”，“<”）
②将D点绕点B顺时针旋转60°得到点E，则线段DB，DC，DA的关系为.

(2)、【知识应用】如图11，AB是圆О的直径， $t a n ∠ A B C = \frac{1}{2}$ ，猜想DA，DB，DC的数量关系，并证明；

(3)、【知识拓展】如图12，已知 $A B = 2$ ， A，B分别是射线DA，DB上的两个动点，以AB为边往外构造等边 $△ A B C$ ，点C在 $∠ M D N$ 内部，若 $∠ D = 120 °$ ，直接写出四边形ADBC面积S的取值范围.

查看试题解析
3. 如图1， $∠ A = 45 ° ， ∠ A B C = 60 °$ ， $A B ∥ M N$ ，点 $C$ 在 $M N$ 上，点 $D$ 在 $A C$ 上， $D E ⊥ M N$ 于点 $E$ ， $D E$ 是半圆 $O$ 的直径，且 $D E = 4$ ， $G$ 为 $\overset{⌢}{D E}$ 上靠近点 $D$ 的三等分点， $F$ 是 $\overset{⌢}{D E}$ 上的动点．

(1)、 $C F$ 的最小值为， $C F$ 的最大值为；

(2)、沿直线 $M N$ 向右平移半圆 $O$ ，若半圆 $O$ 的右移速度为每秒1个单位长，求点 $G$ 在 $△ A B C$ 的区域内部（包括边界）的时长；

(3)、过点 $B$ 作 $B H ⊥ M N$ 于点 $H$ ，且 $B H = \frac{9}{2}$ ，沿直线 $M N$ 向右平移半圆 $O$ ．
①如图2，当点 $E$ 与点 $H$ 重合时，求半圆 $O$ 在 $B C$ 上截得的线段 $R T$ 的长；

②将半圆 $O$ 移动到如图2所示的位置时作为初始位置，将线段 $B E$ 连带半圆 $O$ 按顺时针方向开始旋转，如图3所示，设旋转角为 $α (0 < α < 36 0^{°})$ ．当半圆 $O$ 与 $△ A B C$ 的边相切时，直接写出点 $E$ 运动的路径长．（注：结果保留 $π$ ， $s i n 3 7^{°} = \frac{3}{5}$ ， $s i n 5 3^{°} = \frac{4}{5}$ ）

查看试题解析
4. 新定义：在平面直角坐标系 $x O y$ 中，若几何图形 $G$ 与 $⊙ A$ 有公共点，则称几何图形 $G$ 为 $⊙ A$ 的关联图形，特别地，若 $⊙ A$ 的关联图形 $G$ 为直线，则称该直线为 $⊙ A$ 的关联直线．如图， $∠ M$ 为 $⊙ A$ 的关联图形，直线 $l$ 为 $⊙ A$ 的关联直线．

(1)、已知 $⊙ O$ 是以原点为圆心， $2$ 为半径的圆，下列图形：
$①$ 直线 $y = 2 x + 2$ ； $②$ 直线 $y = - x + 3$ ； $③$ 双曲线 $y = \frac{2}{x}$ ，是 $⊙ O$ 的关联图形的是（请直接写出正确的序号）．

(2)、如图1， $⊙ T$ 的圆心为 $T (1 ， 0)$ ，半径为 $1$ ，直线 $l$ ： $y = - x + b$ 与 $x$ 轴交于点 $N$ ，若直线 $l$ 是 $⊙ T$ 的关联直线，求点 $N$ 的横坐标的取值范围．

(3)、如图2，已知点 $B (0 ， 2)$ ， $C (2 ， 0)$ ， $D (0 ， - 2)$ ， $⊙ I$ 经过点 $C$ ， $⊙ I$ 的关联直线 $H B$ 经过点 $B$ ，与 $⊙ I$ 的一个交点为 $P$ ； $⊙ I$ 的关联直线 $H D$ 经过点 $D$ ，与 $⊙ I$ 的一个交点为 $Q$ ；直线 $H B$ ， $H D$ 交于点 $H$ ，若线段 $P Q$ 在直线 $x = 6$ 上且恰为 $⊙ I$ 的直径，请直接写出点 $H$ 横坐标 $h$ 的取值范围．

查看试题解析
5. 阿基米德（公元前287年-公元前212年），伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家，静态力学和流体静力学的奠基人，阿基米德流传于世的著作有10余种，多为希腊文手稿．下面是《阿基米德全集》中记载的一个命题：如图1， $A B$ 是 $⊙ O$ 的弦，点 $C$ 在 $⊙ O$ 上，且 $C D ⊥ A B$ 于点 $D$ ，在弦 $A B$ 上取点 $E$ ，使 $A D = D E$ ，点 $F$ 是 $\overset{⌢}{B C}$ 上的一点，且 $\overset{⌢}{C F} = \overset{⌢}{A C}$ ，连接 $B F$ ，求证： $B F = B E$ ．
学习小组中的一位同学进行了如下证明：
如图2，连接 $A C$ ， $C E$ ， $B C$
∵ $C D ⊥ A B$ ， $A D = D E$ ．
∴ $∠ C A E = ∠ C E A$
∵ $∠ C A E + ∠ F = 180 °$ ， $∠ C E A + ∠ C E B = 180 °$
∴ $∠ F = ∠ C E B$
……
请完成下列的任务：

(1)、完成上面的证明：

(2)、如图3，将上述问题中弦 $A B$ 改为直径 $A B$ ，若 $C F ∥ A B$ ，求证点 $E$ 是 $A B$ 的中点．

查看试题解析
6. 婆罗摩芨多是公元7世纪古印度伟大的数学家，他在三角形、四边形、零和负数的运算规则，二次方程等方面均有建树，他也研究过对角线互相垂直的圆内接四边形，我们把这类对角线互相垂直的圆内接四边形称为“婆氏四边形”.

(1)、若平行四边形ABCD是“婆氏四边形”，则四边形ABCD是.（填序号）
①矩形；②菱形；③正方形

(2)、如图1，Rt $△$ ABC中，∠BAC=90°，以AB为弦的⊙O交AC于D，交BC于E，连接DE、AE、BD，AB=6， $s i n C = \frac{3}{5}$ ，若四边形ABED是“婆氏四边形”，求DE的长.

(3)、如图2，四边形ABCD为⊙O的内接四边形，连接AC，BD，OA，OB，OC，OD，已知∠BOC+∠AOD=180°.
①求证：四边形ABCD是“婆氏四边形”；
②当AD+BC=4时，求⊙O半径的最小值.

查看试题解析
7. 【证明体验】

(1)、如图1， $⊙ O$ 是等腰 $△ A B C$ 的外接圆， $A B ＝ A C$ ，在 $\overset{⌢}{A C}$ 上取一点 $P$ ，连结 $A P ， B P ， C P$ ，求证： $∠ A P B ＝ ∠ P A C + ∠ P C A$ ；

(2)、【思考探究】
如图2，在（1）条件下，若点 $P$ 为 $\overset{⌢}{A C}$ 的中点， $A B ＝ 6 ， P B ＝ 5$ ，求 $P A$ 的值；

(3)、【拓展延伸】
如图3， $⊙ O$ 的半径为5，弦 $B C ＝ 6$ ，弦 $C P ＝ 5$ ，延长 $A P$ 交 $B C$ 的延长线于点 $E$ ，且 $∠ A B P ＝ ∠ E$ ，求 $A P \cdot P E$ 的值.

查看试题解析
8. 如图，已知 $⊙ O$ 的半径为1，P是平面内一点.

(1)、如图①，若 $O P = 2$ ，过点P作 $⊙ O$ 的两条切线 $P E$ 、 $P F$ ，切点分别为E、F，连接 $E F$ .则 $∠ E P O =$ $°$ ， $E F =$ .

(2)、若点M、N是 $⊙ O$ 上两点，且存在 $∠ M P N = 90 °$ ，则规定点P为 $⊙ O$ 的“直角点”.
①如图②，已知平面内有一点D， $O D = \sqrt{2}$ ，试说明点D是 $⊙ O$ 的“直角点”.
②如图③，直线 $y = \frac{2}{3} x - 2$ 分别与x轴、y轴相交于点A、B，若线段 $A B$ 上所有点都是半径为r的圆的“直角点”，求r的最小值与该圆心的坐标.

查看试题解析
9. 如图
如图①，已知矩形 $A B C D$ ， $A B = 6 ， A D = 8$ .点E从点B出发，沿边 $B C$ 运动至点C停止.以 $D E$ 为直径作 $⊙ O$ ， $⊙ O$ 与对角线 $A C$ 交于点F，连接 $F D$ ， $F E$ .

(1)、如图②，当E运动至终点C时，求 $\frac{F D}{F E}$ 的值；

(2)、试探究：在点E运动的过程中， $\frac{F D}{F E}$ 的值是否为定值？若是，请求出这个值；若不是，请说明理由；

(3)、如图③，以 $F D$ ， $F E$ 为边构造矩形 $D F E G$ ，连接 $C G$ ，求证： $△ A D F ∽ △ C D G$ ，并直接写出在这一运动过程中，点G所经过的路径长.

查看试题解析
10. 【问题呈现】阿基米德折弦定理：阿基米德 $(a r c h i m e d e s$ ，公元前 $287 -$ 公元前212年，古希腊）是有史以来最伟大的数学家之一，他与牛顿、高斯并称为三大数学王子.如图1， $A B$ 和 $B C$ 是 $⊙ O$ 的两条弦（即折线 $A B C$ 是圆的一条折弦）， $B C > A B$ ，点 $M$ 是 $\overset{⌢}{A B C}$ 的中点，则从 $M$ 向 $B C$ 所作垂线的垂足 $D$ 是折弦 $A B C$ 的中点，即 $C D = D B + B A$ .下面是运用“截长法”证明 $C D = D B + B A$ 的部分证明过程.
证明：如图2，在 $C D$ 上截取 $C G = A B$ ，连接 $M A$ 、 $M B$ 、 $M C$ 和 $M G$ .
$∵ M$ 是 $\overset{⌢}{A B C}$ 的中点，
$∴ M A = M C$ ，
又 $∵ ∠ A = ∠ C$ ， $B A = G C$ ，
$∴ △ M A B ≅ △ M C G$ ，
$∴ M B = M G$ ，
又 $∵ M D ⊥ B C$ ，
$∴ B D = D G$ ，
$∴ A B + B D = C G + D G$ 即 $C D = D B + B A$ .

(1)、【理解运用】如图1， $A B$ 、 $B C$ 是 $⊙ O$ 的两条弦， $A B = 4$ ， $B C = 6$ ，点M是 $\overset{⌢}{A B C}$ 的中点， $M D ⊥ B C$ 于点D，则 $B D =$ ；

(2)、【变式探究】如图3，若点M是 $\overset{⌢}{A C}$ 的中点，【问题呈现】中的其他条件不变，判断 $C D$ 、 $D B$ 、 $B A$ 之间存在怎样的数量关系？并加以证明.

(3)、【实践应用】如图4， $B C$ 是 $⊙ O$ 的直径，点A圆上一定点，点D圆上一动点，且满足 $∠ D A C = 45 °$ ，若 $A B = 6$ ， $⊙ O$ 的半径为5，则AD＝.

查看试题解析
11. 综合与实践
问题情境：如图1，将一个底面半径为r的圆锥侧面展开，可得到一个半径为l，圆心角为 $n °$ 的扇形.工人在制作圆锥形物品时，通常要先确定扇形圆心角度数，再度量裁剪材料.

(1)、探索尝试：图1中，圆锥底面周长与其侧面展开图的弧长；（填“相等”或“不相等”）若 $r = 3$ ， $l = 9$ ，则n=.

(2)、解决问题：为操作简便，工人希望能简洁求n的值，请用含r，l的式子表示n；

(3)、拓展延伸：图2是一种纸质圆锥形生日帽， $A B = 6 c m$ ， $l = 6 c m$ ， C是 $P B$ 中点，现要从点A到点C再到点A之间拉一装饰彩带，求彩带长度的最小值.

查看试题解析
12. 概念生成：定义：我们把经过三角形的一个顶点并与其对边所在直线相切的圆叫做三角形的“切接圆”，如图1， $△ A B C$ ， $⊙ O$ 经过点A，并与点A的对边 $B C$ 相切于点D，则该 $⊙ O$ 就叫做 $△ A B C$ 的切接圆.根据上述定义解决下列问题：

(1)、已知， $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $A B = 6$ ， $B C = 10$ .
①如图2，若点D在边 $B C$ 上， $C D = \frac{25}{4}$ ，以D为圆心， $B D$ 长为半径作圆，则 $⊙ D$ 是 $△ A B C$ 的“切接圆”吗？请说明理由.
②在图3中，若点D在 $△ A B C$ 的边上，以D为圆心， $C D$ 长为半径作圆，当 $⊙ D$ 是 $R t △ A B C$ 的“切接圆”时，求 $⊙ D$ 的半径（直接写出答案）.
思维拓展

(2)、如图4， $△ A B C$ 中， $A B = 12$ . $A C = B C = 10$ ，把 $△ A B C$ 放在平面直角坐标系中，使点C落在y轴上，边 $A B$ 落在x轴上.试说明：以抛物线 $y = \frac{1}{16} x^{2} + 4$ 图像上任意一点为圆心都可以作过点C的 $△ A B C$ 的“切接圆”.

查看试题解析
13. 数学兴趣小组在探究圆中图形的性质时，用到了半径是6的若干圆形纸片.

(1)、如图1，一张圆形纸片，圆心为O，圆上有一点A，折叠圆形纸片使得A点落在圆心O上，折痕交 $⊙ O$ 于B、C两点，求 $∠ B A C$ 的度数.

(2)、把一张圆形纸片对折再对折后得到如图扇形，点M是弧 $P Q$ 上一动点.
①如图2，当点M是弧 $P Q$ 中点时，在线段 $O P$ 、 $O Q$ 上各找一点E、F，使得 $△ E F M$ 是等边三角形.试用尺规作出 $△ E F M$ ，不证明，但简要说明作法，保留作图痕迹.

②在①的条件下，取 $△ E F M$ 的内心N，则 $O N =$ .

③如图3，当M在弧 $P Q$ 上三等分点S、T之间（包括S、T两点）运动时，经过兴趣小组探究都可以作出一个 $△ E F M$ 是等边三角形，取 $△ E F M$ 的内心N，请问 $O N$ 的长度是否变化.如变化，请说明理由；如不变，请求出 $O N$ 的长度.

查看试题解析
14. 如图，小明所在学习兴趣小组在探究“如何测量环形花坛面积（阴影部分）”的方法，准备了下列工具：①卷尺；②直木条（足够长）；③T型尺（EF所在的直线垂直平分线段CD）.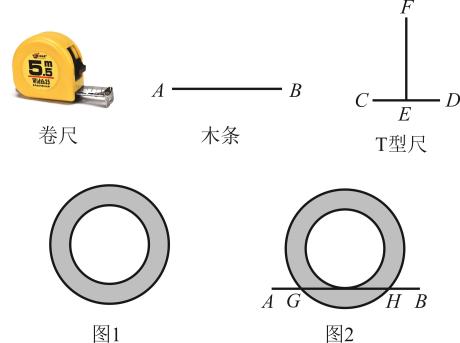

(1)、在图1中，请你用T形尺的原理画出大圆圆心的示意图（保留画图痕迹，不写画法）.

(2)、如图2，小明说：“我只用一根直木条和一个卷尺就可以求出环形花坛的面积，具体做法如下：将直木条放留到与小圆相切，用卷尺量出此时直木条与大圆两交点G，H之间的距离，就可求出环形花坛的面积.”如果测得 $G H = 6 m$ ，请你求出这个环形花坛的面积.

查看试题解析
15. 操作探究题

(1)、已知 $A C$ 是半圆 $O$ 的直径， $∠ A O B = (\frac{180}{n}) °$ （ $n$ 是正整数，且 $n$ 不是3的倍数）是半圆 $O$ 的一个圆心角．
操作：如图1，分别将半圆 $O$ 的圆心角 $∠ A O B = (\frac{180}{n}) °$ （ $n$ 取1、4、5、10）所对的弧三等分（要求：仅用圆规作图，不写作法，保留作图痕迹）；

交流：当 $n = 11$ 时，可以仅用圆规将半圆 $O$ 的圆心角 $∠ A O B = (\frac{180}{n}) °$ 所对的弧三等分吗？

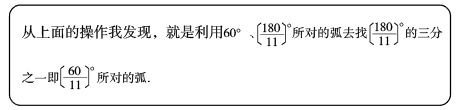
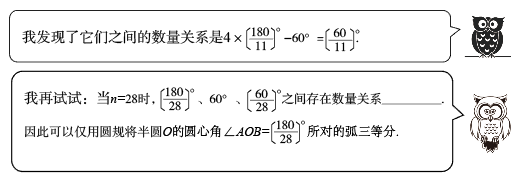
探究：你认为当 $n$ 满足什么条件时，就可以仅用圆规将半圆 $O$ 的圆心角 $∠ A O B = (\frac{180}{n}) °$ 所对的弧三等分？说说你的理由．

(2)、如图2， $⊙ o$ 的圆周角 $∠ P M Q = (\frac{270}{7}) °$ ．为了将这个圆的圆周14等分，请作出它的一条14等分弧 $\overset{⌢}{C D}$ （要求：仅用圆规作图，不写作法，保留作图痕迹）．

查看试题解析