2023年中考数学探究性试题复习13 平行线的判定与性质

试卷更新日期：2023-05-20 类型：三轮冲刺

进入出卷网下载

一、综合题

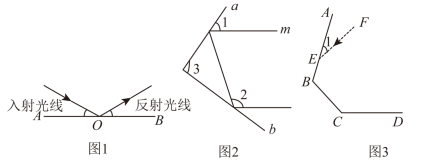
1. 【学习新知】射到平面镜上的光线 $($ 入射光线 $)$ 和反射后的光线 $($ 反射光线 $)$ 与平面镜所夹的角相等，如图1， $A B$ 是平面镜，若入射光线与水平镜面夹角为 $∠ 1$ ，反射光线与水平镜面夹角为 $∠ 2$ ，则 $∠ 1 = ∠ 2$ ．

(1)、【初步应用】如图，一束光线 $m$ 射到平面镜 $a$ 上，被 $a$ 反射到平面镜 $b$ 上，又被 $b$ 反射，若被 $b$ 反射出的光线 $n$ 与光线 $m$ 平行，且 $∠ 1 = 50 °$ ，则 $∠ 2 =$ ， $∠ 3 =$ ；

(2)、【猜想验证】由（1），请你猜想：当两平面镜 $a$ 、 $b$ 的夹角 $∠ 3 =$ ▲ 时，可以使任何射到平面镜 $a$ 上的光线 $m$ ，经过平面镜 $a$ 、 $b$ 的两次反射后，入射光线 $m$ 与反射光线 $n$ 平行，请说明理由；

(3)、【拓展探究】如图 $3$ ，有三块平面镜 $A B$ ， $B C$ ， $C D$ ，入射光线 $E F$ 与镜面 $A B$ 的夹角 $∠ 1 = α °$ ，镜面 $A B$ 、 $B C$ 的夹角 $∠ B = 120 °$ ，已知入射光线从镜面 $A B$ 开始反射，经过 $n (n$ 为正整数， $n \leq 3)$ 次反射，当第 $n$ 次反射光线与入射光线 $E F$ 平行时，请直接写出 $∠ B C D$ 的度数． $($ 可用含有 $α$ 的代数式表示)

查看试题解析
2. 如图
【学习新知】：
射到平面镜上的光线（入射光线）和反射后的光线（反射光线）与平面镜所夹的角相等．如图1， $A B$ 是平面镜，若入射光线与水平镜面夹角为 $∠ 1$ ，反射光线与水平镜面夹角为 $∠ 2$ ，则 $∠ 1 = ∠ 2$ ．

(1)、【初步应用】：
生活中我们可以运用“激光”和两块相交的平面镜进行测距．如图2当一束“激光” $D O_{1}$ 射入到平面镜 $A B$ 上、被平面镜 $A B$ 反射到平面镜 $B C$ 上，又被平面镜 $B C$ 反射后得到反射光线 $O_{2} E$ ．回答下列问题：
①当 $D O_{1} ∥ E O_{2}$ ， $∠ E O_{2} C = 60 °$ （即 $∠ 4 = 60 °$ ）时，求 $∠ D O_{1} O_{2}$ 的度数．
②当 $∠ B = 90 °$ 时，任何射入平面镜 $A B$ 上的光线 $D O_{1}$ 经过平面镜 $A B$ 和 $B C$ 的两次反射后，入射光线 $D O_{1}$ 与反射光线 $O_{2} E$ 总是平行的．请你根据所学过的知识及新知说明．
（提示：三角形的内角和等于 $180 °$ ）

(2)、【拓展探究】：
如图3，有三块平面镜 $A B$ ， $B C$ ， $C D$ ，入射光线 $E O_{1}$ 经过三次反射，得到反射光线 $O_{3} F$ ，已知 $∠ 1 = 36 °$ ， $∠ B = 120 °$ ，若要使 $E O_{1} ∥ O_{3} F$ ，求 $∠ C$ 的度数．

查看试题解析
3. 将一副三角板中的两个直角顶点 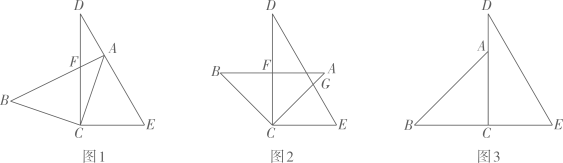$C$ 叠放在一起，其中 $∠ A = ∠ B = 45 °$ ， $∠ D = 30 °$ ， $∠ E = 60 °$

(1)、操作发现：如图1，当点 $A$ 落在线段 $D E$ 上时，写出图中相等的角（写出三对即可）；

(2)、问题解决：如图2，若线段 $A C$ 与 $D E$ 交于点 $G$ ．
①若 $∠ B C E = 3 ∠ A C D$ 时，求 $∠ B C D$ 的度数；
②当 $∠ B C D$ 为何值时，使线段 $C G$ 最短；

(3)、深化拓展：如图3，将三角板 $A B C$ 绕点 $C$ 顺时针转动，直到边 $B C$ 与 $C E$ 重合即停止，转动的过程中当两块三角板恰有两边平行时，请直接写出 $∠ A C D$ 的度数．

查看试题解析
4. 几何模型在解题中有着重要作用，例如美味的“猪蹄模型”．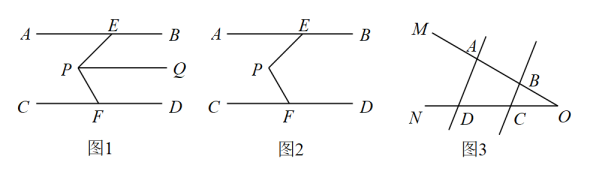

(1)、导入：如图1，已知 $A B ∥ P Q ∥ C D$ ，如果 $∠ A E P = 45 °$ ， $∠ C F P = 60 °$ ，则 $∠ E P F =$ $°$ ；

(2)、发现：如图2，直线 $A B ∥ C D$ ，请判断 $∠ A E P$ 与 $∠ C F P$ ， $∠ E P F$ 之间的数量关系，并说明理由；

(3)、运用：如图3，已知 $A D ∥ B C$ ， P在射线 $O M$ 上运动（点P与点A、B、O三点不重合）， $∠ A D P = α$ ， $∠ B C P = β$ ，请用含 $α$ 、 $β$ 的代数式表示 $∠ C P D$ ，并说明理由．

查看试题解析
5. [阅读探究]如图(a)所示，已知AB∥CD，点E，F分别是AB，CD上的点，点M在AB，CD两平行线之间，∠AEM=45°，∠CFM=25°，求∠EMF的度数．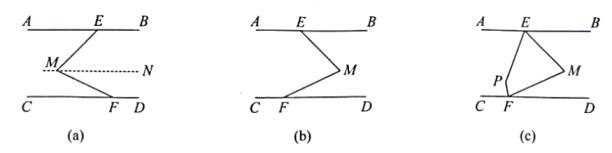
解：如图(a)所示，过点M作MN∥AB．
∵AB∥CD，
∴MN∥CD．
∴∠EMN= CAEM=45°，∠FMN=∠CFM= 25°．
∴∠EMF=∠EMN+∠FMN=45°+25°=70°．

(1)、从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将∠AEM和∠CFM“凑”在一起，得出角之间的关系，使问题得以解决．通过进一步研究，我们可以发现图(a)中∠AEM，∠EMF和∠CFM之间存在一定的数量关系，请直接写出它们之间的数量关系：

(2)、[方法运用]如图(b)所示，已知AB∥CD，点E，F分别在直线AB，CD上，点M在AB，CD之间，求∠AEM，∠EMF和∠CFM之间的数量关系．

(3)、[应用拓展]如图(C)所示，在图(b)的条件下，分别作LAEM和∠CFM的角平分线EP，FP，交于点P (交点P在AB，CD之间)．若∠EMF=60°，求∠EPF的度数．．

查看试题解析
6. 【学习新知】射到平面镜上的光线（入射光线）和反射后的光线（反射光线）与平面镜所夹的角相等．如图1，若入射光线与水平镜面夹角为 $∠ 1$ ，反射光线与水平镜面夹角为 $∠ 2$ ，则 $∠ 1 = ∠ 2$ ．

(1)、【初步应用】如图2，有两块平面镜 $A B$ ， $B C_{1}$ ，入射光线 $D O_{1}$ 经过两次反射，得到反射光线 $O_{2} E$ ，若 $∠ B = 90 °$ ，证明： $D O_{1} ∥ O_{2} E$ ；

(2)、【拓展探究】如图3，有三块平面镜 $A B$ ， $B C$ ， $C D$ ，入射光线 $E O_{1}$ 经过三次反射，得到反射光线 $O_{3} F$ ，已知 $∠ 1 = 36 °$ ， $∠ B = 120 °$ ，若要使 $E O_{1} ∥ O_{3} F$ ，则 $∠ C$ 为多少度？

查看试题解析
7. 如图

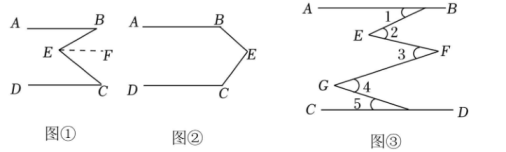(1)、问题发现：
如图①，直线AB∥CD，连接BE，CE，可以发现∠B+∠C=∠BEC．请把下面的证明过程补充完整：
证明：过点E作EF∥AB，
∵AB∥DC (已知)
∴EF∥DC（）．
∴∠C=∠CEF．（）．
∵EF∥AB，
∴∠B=∠BEF(同理)．
∴∠B+∠C= ▲ (等量代换)．即∠B+∠C=∠BEC．

(2)、拓展探究：
如果点E运动到图②所示的位置，其他条件不变，说明：∠B+∠C+∠BEC=360°．

(3)、解决问题：如图③，AB∥DC，E、F、G是AB与CD之间的点，直接写出∠1，∠2，∠3，∠4，∠5之间的数量关系．

查看试题解析
8. 如图①，直线 $l_{1} ∥ l_{2}$ ，直线EF和直线 $l_{1}$ 、 $l_{2}$ 分别交于C、D两点，点A、B分别在直线 $l_{1}$ 、 $l_{2}$ 上，点P在直线EF上，连接PA、PB.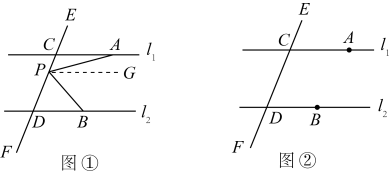

(1)、如图①，若点P在线段CD上， $∠ P A C = 15 °$ ， $∠ P B D = 40 °$ ，求 $∠ A P B$ 的大小；

(2)、猜想：如图①，若点P在线段CD上移动，直接写出 $∠ P A C$ 、 $∠ A P B$ 、 $∠ P B D$ 之间的数量关系；

(3)、探究：如图②，若点P不在线段CD上，则（2）中的数量关系还成立吗？若成立，请说明理由；若不成立，请写出正确的结论并说明理由.

查看试题解析
9. 在一个数学活动中，若身旁没有量角器或者三角尺，又需要作 $60 °$ ， $30 °$ ， $15 °$ 的角，可以采用如下的方法：
【操作感知】

第一步：对折矩形纸片 $A B C D$ ，使 $A D$ 与 $B C$ 重合，得到折痕 $E F$ ，把纸片展开.

第二步；再一次折叠纸片，使点 $A$ 落在 $E F$ 上，并使折痕经过点 $B$ ，得到折痕 $B M$ ，同时得到线段 $B N$ （如图1）.

(1)、【猜想论证】
写出图1中一个 $30 °$ 的角：.

(2)、若延长 $M N$ 交 $B C$ 于点 $P$ ，如图 $2$ 所示，试判断 $△ B M P$ 的形状，并证明.

(3)、【迁移探究】
小华将矩形纸片换正方形纸片，继续探究，过程如下：
将正方形纸片 $A B C D$ 按照 $“$ 操作感知 $”$ 的方式操作，并延长 $M N$ 交 $C D$ 于点 $Q$ ，连接 $B Q$ .当点 $N$ 在 $E F$ 上时， $D M = 2$ ，求正方形的边长.

查看试题解析
10. 在平面直角坐标系中， $A (- 4 ， 3)$ ， $B (4 ， 3)$ ，动点 $P$ 在射线 $A B$ 上从点 $A$ 开始以每秒1个单位长度的速度从左向右运动.

(1)、当点 $P$ 运动的时间为2秒时，点 $P$ 的坐标是；

(2)、如图1， $Q (1 ， 2)$ ，在点 $P$ 运动的过程中，三角形 $P O Q$ 的面积能等于3吗？若能，请求出点 $P$ 运动的时间；若不能，请说明理由.

(3)、如图2， $A B$ 与 $y$ 轴交于点 $M$ ，将线段 $A B$ 向下平移得到 $C D$ ， $C D$ 与 $y$ 轴交于点 $N$ ，点 $E$ 为线段 $M B$ 上任意一点，点 $G$ 为线段 $N D$ 上任意一点， $∠ E O G = 130 °$ .点 $F$ 为线段 $M B$ 与线段 $N D$ 之间一点，连接 $E F$ ， $G F$ ，且 $∠ B E F = \frac{1}{3} ∠ B E O$ ， $∠ E F G = 80 °$ .试写出 $∠ F G O$ 与 $∠ F G D$ 之间的数量关系，并证明你的结论.

查看试题解析
11. 问题提出：一条线段沿某个方向平移一段距离后与原线段构成一个平行四边形.我们可以利用这一性质，将有些条件通过平移集中在一起来解决一些几何问题.

如图①，两条长度相等的线段 $A B$ 和 $C D$ 相交于O点， $∠ A O C = 60 °$ ，直线 $A C$ 与直线 $B D$ 的夹角为 $α$ ，求线段 $A C$ 、 $B D$ 、 $A B$ 满足的数量关系.

分析：考虑将 $A C$ 、 $B D$ 和 $A B$ 集中到同一个三角形中，以便运用三角形的知识寻求三条线段的数量关系：

如图②，作 $C E / / A B$ 且 $C E = A B$ ，则四边形 $A B E C$ 是平行四边形，从而 $A C = B E$ ；

由于 $C D = A B = C E$ ， $∠ E C D = ∠ A O C = 60 °$ ，所以 $△ E C D$ 是等边三角形，故 $E D = A B$ ；

通过平行又求得 $∠ E B D = 180 ° - α$ .

在 $△ B E D$ 中，研究三条线段的大小关系就可以了.

(1)、如图②，若 $A C = 2 \sqrt{3}$ ， $B D = 6$ ， $α = 30 °$ ，请直接写出线段 $A B$ 的长；

(2)、问题解决：如图③，矩形 $A B C D$ 中，E、F分别是 $A D$ 、 $C D$ 上的点，满足 $A E = C D$ ， $D E = C F$ ，求证： $A F = \sqrt{2} C E$ ；

(3)、拓展应用：如图④， $△ A B C$ 中， $∠ A = 45 °$ ， D、E分别在 $A C$ 、 $A B$ 上， $B D$ 、 $C E$ 交于点O， $B D = C E$ ， $∠ B O C = 120 °$ ，若 $B E = 4$ ， $C D = 3 \sqrt{2}$ ，则 $B D =$ .

查看试题解析
12. 问题情境：如图1， $A B ∥ C D$ ， $∠ 1 = 40 °$ ， $∠ 2 = 35 °$ ，求 $∠ B P C$ 的度数.小明的思路是过点 $P$ 作 $P E ∥ A B$ ，通过平行线的性质来求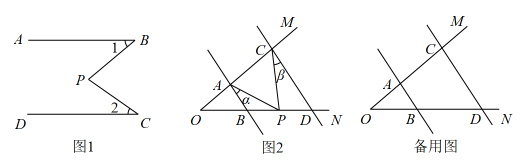 $∠ B P C$ .

(1)、按照小明的思路，则 $∠ B P C$ 的度数为；

(2)、问题迁移：如图2， $A B ∥ C D$ ，点 $P$ 在射线 $O N$ 上运动，记 $∠ P A B = α$ ， $∠ P C D = β$ .当点 $P$ 在 $B$ 、 $D$ 两点之间运动时，问 $∠ A P C$ 与 $α$ 、 $β$ 之间有何数量关系？请说明理由；

(3)、在（2）的条件下，如果点 $P$ 不在 $B$ 、 $D$ 两点之间运动时（点 $P$ 与点 $O$ 、 $B$ 、 $D$ 三点不重合），写出 $∠ A P C$ 与 $α$ 、 $β$ 之间的数量关系，并说明理由.

查看试题解析
13. 综合与实践：如图

(1)、模型启迪：如图1，在 $△ A B C$ 中，D为 $B C$ 边的中点，连接 $A D$ 并延长至点H，使 $D H = A D$ ，连接 $C H$ ．由 $∠ A D B = ∠ C D H$ ，得 $△ A D B ≌ △ H D C$ ，则 $A B$ 与 $C H$ 的数量关系为，位置关系为．

(2)、模型探索：如图2，在 $△ A B C$ 中， $A P$ 平分 $∠ B A C$ ， D为 $B C$ 边的中点，过点D作 $D Q ∥ A P$ ，交 $C A$ 的延长线于点Q，交 $A B$ 边于点K．试判断 $B K$ 与 $C Q$ 的数量关系，并说明理由．

(3)、如图3，在 $△ A B C$ 中，D为 $B C$ 边的中点，连接 $A D$ ， E为 $A C$ 边上一点，过点E作 $E G ⊥ A D$ 于点G，连接 $B E$ 交 $A D$ 于点F，且 $B F = A C$ ．求证： $A G = G F$ ．

(4)、模型应用：如图4，在（3）的条件下，延长 $A C$ 至点N，使 $A N = A B$ ，连接 $B N$ ，交 $A D$ 的延长线于点M．若 $A B = 7$ ， $A C = 5$ ， $∠ C A D = 60 °$ ，请直接写出线段 $D M$ 的长．

查看试题解析
14. 【教材再现】
在初中数学教材中有这样一个基本事实：两条直线被一组平行线所截，所得的对应线段成比例.如图1，直线 $l_{1} ∥ l_{2}$ ，直线m和直线n分别与直线 $l_{1}$ 和直线 $l_{2}$ 相交于点A，点B，点F，点D，直线m和直线n相交于点E，则 $\frac{B E}{A B} = \frac{D E}{F D}$ ；
【探究发现】
如图2，在 $△ A B C$ 中， $A C = B C = 3$ ， $∠ C = 90 °$ ，点D在边 $B C$ 上（不与点B，点C重合），连接 $A D$ ，点E在边 $A B$ 上， $∠ E D B = ∠ A D C$ .

(1)、求证： $\frac{B E}{A B} = \frac{D E}{A D}$ ；

(2)、当 $\frac{D E}{A D} = \frac{1}{2}$ 时，直接写出 $A D$ 的长；

(3)、点H在射线AC上，连接EH交线段 $A D$ 于点G，当 $C H = 1$ ，且 $∠ A E H = ∠ B E D$ 时，直接写出 $\frac{B E}{A B}$ 的值.

查看试题解析
15. 阅读下面材料：
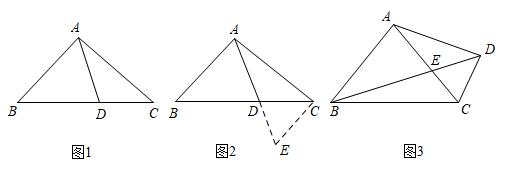
小腾遇到这样一个问题：如图1，在△ABC中，点D在线段BC上，∠BAD＝75°，∠CAD＝30°，AD＝2，BD＝2DC，求AC的长.
小腾发现，过点C作CE∥AB，交AD的延长线于点E，经过推理和计算能够使问题得到解决，如图2.

(1)、请回答：∠ACE的度数为， AC的长为.

(2)、参考小腾思考问题的方法，解决问题：
如图3，在四边形ABCD中，∠BAC＝90°，∠CAD＝30°，∠ADC＝75°，AC与BD交于点E，AE＝2，BE＝2ED，求BC的长.

查看试题解析
16. 课题学习：平行线的“等角转化”功能.

(1)、阅读理解：如图1，已知点A是 $B C$ 外一点，连接 $A B$ 、 $A C$ ，求 $∠ B + ∠ B A C + ∠ C$ 的度数.阅读并补充下面推理过程.
解：过点A作 $E D ∥ B C$ ，
$∴$ $∠ B =$ ▲ ， $∠ C$ ▲ ，
$∵$ $∠ E A B + ∠ B A C + ∠ D A C = 180 °$ ，
$∴$ $∠ B + ∠ B A C + ∠ C = 180 °$ .
解题反思：从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将 $∠ B A C$ 、 $∠ B$ 、 $∠ C$ “凑”在一起，得出角之间的关系，使问题得以解决.

(2)、方法运用：如图2，已知 $A B ∥ E D$ ，求 $∠ B + ∠ B C D + ∠ D$ 的度数；

(3)、深化拓展：已知 $A B ∥ C D$ ，点C在点D的右侧， $∠ A D C = 50 °$ ， $B E$ 平分 $∠ A B C$ ， $D E$ 平分 $∠ A D C$ ， $B E$ ， $D E$ 所在的直线交于点E，点E在直线 $A B$ 与 $C D$ 之间.
①如图3，点B在点A的左侧，若 $∠ A B C = 36 °$ ，求 $∠ B E D$ 的度数.

②如图4，点B在点A的右侧，且 $A B < C D$ ， $A D < B C$ .若 $∠ A B C = n °$ ，求 $∠ B E D$ 度数.（用含n的代数式表示）

查看试题解析