2023年中考数学探究性试题复习12 二次函数

试卷更新日期：2023-05-20 类型：三轮冲刺

进入出卷网下载

一、综合题

1. 在平面直角坐标系中，如果一个点的横坐标与纵坐标相等，则称该点为“不动点”
例如 $(- 3 ， - 3)$ 、 $(1 ， 1)$ 、 $(2023 ， 2023)$ 都是“不动点”，已知双曲线 $y = \frac{9}{x}$

(1)、下列说法错误的是（）

A、直线 $y = x$ 的图象上有无数个“不动点” B、函数 $y = \frac{- 1}{x}$ 的图象上没有“不动点” C、直线 $y = x + 1$ 的图象上有无数个“不动点” D、函数 $y = x^{2}$ 的图象上有两个“不动点”

(2)、求双曲线 $y = \frac{9}{x}$ 上的“不动点”；

(3)、若抛物线 $y = a x^{2} - 3 x + c$ （ $a$ 、 $c$ 为常数）上有且只有一个“不动点”，
①当 $a > 1$ 时，求 $c$ 的取值范围．
②如果 $a = 1$ ，过双曲线 $y = \frac{9}{x}$ 图象上第一象限的“不动点”作平行于 $x$ 轴的直线 $l$ ，若抛物线上有四个点到 $l$ 的距离为 $m$ ，直接写出 $m$ 的取值范围．

查看试题解析
2. 综合与探究．
如图1，抛物线 $y = a x^{2} + b x + 2 (a \neq 0)$ 经过 $(2 ， - 3)$ ， $(- 2 ， 3)$ ，且与x轴交于A，B两点（点B在点A的右侧），与y轴交于点C，连接 $A C$ ， $B C$ ．

(1)、求抛物线的表达式．

(2)、求证： $△ A O C ∼ △ C O B$ ．

(3)、如图2，动点P从点B出发，沿着线段 $B A$ 以每秒1个单位长度的速度向终点A运动；同时，动点Q从点A出发，以相同的速度沿着线段 $A C$ 向终点C运动，当其中一个动点到达终点时，另一个动点也随之停止运动，连接 $P Q$ ，设P，Q运动的时间为t秒，在点P，Q运动的过程中， $△ A P Q$ 是否成为等腰三角形？若能，请求出t的值；若不能，请说明理由．

查看试题解析
3. 定义：若一个函数图象上存在横、纵坐标相等的点，则称该点为这个函数图象的“等值点”，例如：点 $(1 ， 1)$ 是函数 $y = \frac{1}{2} x + \frac{1}{2}$ 的图像的“等值点”.

(1)、分别判断函数 $y = x + 1$ ， $y = x^{2} - x$ 的图像上是否存在“等值点”？如果存在，求出“等值点”的坐标；如果不存在，说明理由；

(2)、设函数 $y = \frac{3}{x} (x > 0)$ ， $y = - x + b$ 的图像的“等值点”分别为点 $A$ ， $B$ ，过点 $B$ 作 $B C ⊥ x$ 轴，垂足为 $C$ .当 $△ A B C$ 的面积为3时，求 $b$ 的值；

(3)、若函数 $y = x^{2} - 2 (x \geq m)$ 的图像记为 $W_{1}$ ，将其沿直线 $x = m$ 翻折后的图像记为 $W_{2}$ ，当 $W_{1}$ ， $W_{2}$ 两部分组成的图像上恰有2个“等值点”时，直接写出 $m$ 的取值范围.

查看试题解析
4. 如图1，对于平面上小于或等于 $90 °$ 的 $∠ M O N$ ，我们给出如下定义：若点P在 $∠ M O N$ 的内部或边上，作 $P E ⊥ O M$ 于点E， $P F ⊥ O N$ 于点F，则将 $P E + P F$ 称为点P与 $∠ M O N$ 的“点角距”，记作 $d (∠ M O N ， P)$ .如图2，在平面直角坐标系 $x O y$ 中，x、y正半轴所组成的角记为 $∠ x O y$ .

(1)、已知点 $A (4 ， 0)$ 、点 $B (3 ， 1)$ ，则 $d (∠ x O y ， A) =$ ， $d (∠ x O y ， B) =$ .

(2)、若点P为 $∠ x O y$ 内部或边上的动点，且满足 $d (∠ x O y ， P) = 4$ ，在图2中画出点P运动所形成的图形.

(3)、如图3与图4，在平面直角坐标系 $x O y$ 中，射线 $O T$ 的函数关系式为 $y = \frac{4}{3} x (x \geq 0)$ .
①在图3中，点C的坐标为 $(4 ， 1)$ ，试求 $d (∠ x O T ， C)$ 的值；

②在图4中，抛物线 $y = - \frac{1}{2} x^{2} + 2 x + c$ 经过 $A (5 ， 0)$ ，与射线 $O T$ 交于点D，点Q是A，D两点之间的抛物线上的动点（点Q可与A，D两点重合），求c的值和当 $d (∠ x O T ， Q)$ 取最大值时点Q的坐标.

查看试题解析
5. 如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法： $S_{△ A B C} = \frac{1}{2} a h$ ，即三角形面积等于水平宽与铅垂高乘积的一半.

解答下列问题：

如图2，抛物线顶点坐标为点C(1，4)，交x轴于点A(3，0)，交y轴于点B.

(1)、求抛物线和直线AB的解析式；

(2)、点P是抛物线(在第一象限内)上的一个动点，连接PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及 $S_{Δ C A B}$ ；

(3)、是否存在一点P，使S_△PAB= $\frac{9}{8}$ S_△CAB，若存在，求出P点的坐标；若不存在，请说明理由.

查看试题解析
6. 定义：若直线 $y = - 1$ 与开口向下的抛物线有两个交点，则这两个交点之间的距离叫做这条抛物线的“反碟长”．如图，已知抛物线 $L_{1}$ ： $y = - x^{2}$ 与直线 $y = - 1$ 相交于 $P$ ， $Q$ ．

(1)、抛物线 $L_{1}$ 的“反碟长” $P Q =$ ．

(2)、抛物线随其顶点沿直线 $y = \frac{1}{2} x$ 向上平移，得到抛物线 $L_{2}$ ．
①当抛物线 $L_{1}$ 的顶点平移到点 $(6 ， 3)$ ，抛物线 $L_{2}$ 的解析式是 ▲ ．抛物线 $L_{2}$ 的“反碟长”是 ▲ ．
②若抛物线 $L_{2}$ 的“反碟长”是一个偶数，则其顶点的纵坐标可能是 ▲ ．（填写所有正确的选项）
A.15 B.16 C.24 D.25
③当抛物线 $L_{2}$ 的顶点 $A$ 和抛物线 $L_{2}$ 与直线 $y = - 1$ 的两个交点 $B$ ， $C$ 构成一个等边三角形时（点 $B$ 在点 $C$ 左右），求点 $A$ 的坐标．

查看试题解析
7. 综合与探究
已知抛物线 $C_{1} ： y = a x^{2} + b x - 5 (a \neq 0)$ ．

(1)、当抛物线经过 $(- 1 ， - 8)$ 和 $(1 ， 0)$ 两点时，求抛物线的函数表达式．

(2)、当 $b = 4 a$ 时，无论a为何值，直线 $y = m$ 与抛物线 $C_{1}$ 相交所得的线段 $A B$ （点A在点 B的左侧）的长度始终不变，求m的值和线段 $A B$ 的长．

(3)、在（2）的条件下，将抛物线 $C_{1}$ 沿直线 $y = m$ 翻折得到抛物线 $C_{2}$ ，抛物线 $C_{1}$ ， $C_{2}$ 的顶点分别记为G，H．是否存在实数a使得以A，B，G，H为顶点的四边形为正方形？若存在，直接写出a的值；若不存在，请说明理由．

查看试题解析
8. 如图，抛物线 $y ＝ - x^{2} + b x + 3$ 与x轴交于点 $A ， B ，$ 与y轴交于点C，点A的坐标为 $(- 1 ， 0)$ ．

(1)、求b的值和点B，C的坐标；

(2)、若点D为 $O C$ 的中点，点P为第一象限内抛物线上的一点，过点P作 $P H ⊥ x$ 轴，垂足为H， $P H$ 与 $B C ， B D$ 分别交于点 $E ， F$ ，且 $P E = E F = F H$ ，求点P的坐标；

(3)、若直线 $y = n x + n （ n \neq 0 ）$ 与抛物线交于 $M (x_{1} ， y_{1}) ， N (x_{2} ， y_{2})$ 两点，且有一个交点在第一象限，其中 $x_{1} < x_{2}$ ，若 $x_{2} - x_{1} > 3 ， y_{2} > y_{1} ，$ 结合函数图象，探究n的取值范围．

查看试题解析
9. 一张矩形纸片ABCD（如图1），AB=6，AD=3.点E是BC边上的一个动点，将△ABE沿直线AE折叠得到△AEF，延长AE交直线CD于点G，直线AF与直线CD交于点Q.

【初步探究】

(1)、求证：△AQG是等腰三角形；

(2)、记FQ=m，当BE=2CE时，计算m的值；

(3)、【深入探究】
将矩形纸片放入平面直角坐标系中（如图2所示），点B与点O重合，边OC、OA分别与x轴、y轴正半轴重合.点H在OC边上，将△AOH沿直线AH折叠得到△APH.
①当AP经过CD的中点N时，求点P的坐标；
②在①的条件下，已知二次函数y=-x²+bx+c的图象经过A、D两点.若将直线AH右侧的抛物线沿AH对折，交y轴于点M，请求出AM的长度.

查看试题解析
10. 定义：两个二次项系数之和为 $1$ ，对称轴相同，且图像与y轴交点也相同的二次函数互为友好同轴二次函数.例如： $y = 2 x^{2} + 4 x - 5$ 的友好同轴二次函数为 $y = - x^{2} - 2 x - 5$ .

(1)、函数 $y = \frac{1}{4} x^{2} - 2 x + 3$ 的友好同轴二次函数为.

(2)、当 $- 1 \leq x \leq 4$ 时，函数 $y = (1 - a) x^{2} - 2 (1 - a) x + 3$ $(a \neq 0 且 a \neq 1)$ 的友好同轴二次函数有最大值为 $5$ ，求 $a$ 的值.

(3)、已知点 $(m ， p) ， (m ， q)$ 分别在二次函数 $y_{1} = a x^{2} + 4 a x + c (a > \frac{1}{2} 且 a \neq 1 ）$ 及其友好同轴二次函数 $y_{2}$ 的图像上，比较 $p ， q$ 的大小，并说明理由.

查看试题解析
11. 如图1，在平面直角坐标系中，四边形AOBC为矩形，BC= $2 \sqrt{3}$ ， ∠BOC=60°，D为BC中点.某反比例函数过点D，且与直线OC交于点E.

(1)、点E的坐标为.

(2)、好奇的小明在探索一个新函数.若点P为x轴上一点，过点P作x轴的垂线交直线AC于点Q，交该反比例函数图象于点R.若y′=PQ+PR，点P横坐标为x. $y^{'}$ 关于x的图像如图2，其中图像最低点F、G横坐标分别为（ $\sqrt{2}$ ， $\sqrt{2}$ ）、（ $- \sqrt{2}$ ， $- \sqrt{2}$ ）.
①求 $y^{'}$ 与x之间的函数关系式.
②写出该函数的两条性质.

(3)、已知1<x<4
①若关于x的方程x²－4x－m=0有解，求m的取值范围.小明思考过程如下：由x²－4x－m=0得m=x²－4x，m是关于x的二次函数，根据x的范围可以求出m的取值范围.请你完成解题过程.
②若关于x的方程 $\sqrt{6} x^{2} - m x + 2 \sqrt{6} = 0$ 有解，请直接写出m的取值范围.

查看试题解析
12. 如图，抛物线 $y = - x^{2} + b x + c$ 与x轴交于 $A (- 1 ， 0)$ ， $B (3 ， 0)$ 两点，与y轴交于点C，点D是抛物线的顶点.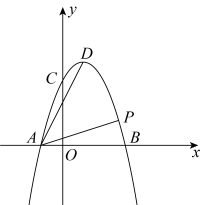

(1)、求抛物线解析式；

(2)、求开口向下的二次函数的最大值时采用的步骤是：第一，求出二次函数的顶点坐标 $(- \frac{b}{2 a} ， \frac{4 a c - b^{2}}{4 a})$ ；第二，确定自变量x的取值范围；第三判定 $x = - \frac{b}{2 a}$ 是否在其范围内，若在，则最大值是顶点纵坐标，若不在，要根据其增减性求最大值，即当 $m \leq x \leq n < - \frac{b}{2 a} (m < n)$ 时， $x = n$ 时，y最大；当 $- \frac{b}{2 a} < m \leq x \leq n$ $(m < n)$ 时， $x = m$ 时，y最大.若 $t < 0$ ， $t \leq x \leq t + 1$ 时，二次函数 $y = - x^{2} + b x + c$ 的最大值是t，求t的值.

(3)、如图，若点P是第一象限抛物线上一点，且 $∠ D A P = 45 °$ ，求点P的坐标.

查看试题解析
13. 在平面直角坐标系中，如果点 $P$ 的横坐标和纵坐标相等，则称点 $P$ 为和谐点，例如：点 $(1 ， 1)$ ， $(\frac{1}{2} ， \frac{1}{2})$ ， $(- \sqrt{2} ， - \sqrt{2})$ ， ……都是和谐点．

(1)、判断函数 $y = 2 x + 1$ 的图象上是否存在和谐点，若存在，求出其和谐点的坐标；

(2)、若二次函数 $y = a x^{2} + 6 x + c (a \neq 0)$ 的图象上有且只有一个和谐点 $(\frac{5}{2} ， \frac{5}{2})$ ．
①求 $a$ ， $c$ 的值；

②若 $1 \leq x \leq m$ 时，函数 $y = a x^{2} + 6 x + c + \frac{1}{4} (a \neq 0)$ 的最小值为－1，最大值为3，求实数 $m$ 的取值范围．

查看试题解析
14. 探索发现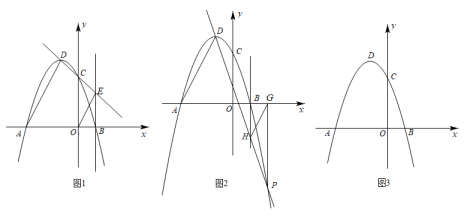

(1)、在平面直角坐标系中，抛物线y＝ax²+bx+3（a≠0）与x轴交于点A（﹣3，0），B（1，0），与y轴交于点C，顶点为点D，连接AD．
①如图1，直线DC交直线x＝1于点E，连接OE．求证：AD∥OE；
②如图2，点P（2，﹣5）为抛物线y＝ax²+bx+3（a≠0）上一点，过点P作PG⊥x轴，垂足为点G．直线DP交直线x＝1于点H，连接HG．求证：AD∥HG；

(2)、通过上述两种特殊情况的证明，你是否有所发现？请仿照（1）写出你的猜想，并在图3上画出草图．在平面直角坐标系中，抛物线y＝ax²+bx+3（a≠0）与x轴交于点A（﹣3，0），B（1，0），顶点为点D．点M为该抛物线上一动点（不与点A，B，D重合），
猜想：作MN⊥x轴于N，直线DM交直线x=1于Q，则QN∥AD，证明见解析

查看试题解析
15. 【发现问题】
小明在练习簿的横线上取点 $O$ 为圆心，相邻横线的间距为半径画圆，然后半径依次增加一个间距画同心圆，描出了同心圆与横线的一些交点，如图1所示，他发现这些点的位置有一定的规律．
【提出问题】
小明通过观察，提出猜想：按此步骤继续画圆描点，所描的点都在某二次函数图象上．

(1)、【分析问题】
小明利用已学知识和经验，以圆心 $O$ 为原点，过点 $O$ 的横线所在直线为 $x$ 轴，过点 $O$ 且垂直于横线的直线为 $y$ 轴，相邻横线的间距为一个单位长度，建立平面直角坐标系，如图2所示．当所描的点在半径为5的同心圆上时，其坐标为．

(2)、【解决问题】
请帮助小明验证他的猜想是否成立．

(3)、【深度思考】
小明继续思考：设点 $P (0 ， m)$ ， $m$ 为正整数，以 $O P$ 为直径画 $⊙ M$ ，是否存在所描的点在 $⊙ M$ 上．若存在，求 $m$ 的值；若不存在，说明理由．

查看试题解析