2023年中考数学探究性试题复习3 新定义

试卷更新日期：2023-05-20 类型：三轮冲刺

进入出卷网下载

一、单选题

1. 定义：在平面直角坐标系中，若点A满足横、纵坐标都为整数，则把点A叫做“整点”．如：B（3，0）、C（-1，3）都是“整点”．抛物线y＝ax²-2ax+a+2（a＜0）与x轴交于点M，N两点，若该抛物线在M、N之间的部分与线段MN所围的区域（包括边界）恰有5个整点，则a的取值范围是（）

A、-1≤a＜0 B、-2≤a＜-1 C、-1≤a＜ $- \frac{1}{2}$ D、-2≤a＜0

查看试题解析
2. 对于任意实数m，n，如果满足 $\frac{m}{2} + \frac{n}{4} = \frac{m + n}{2 + 4}$ ，那么称这一对数m，n为“完美数对”，记为 $(m ， n)$ .若 $(a ， b)$ 是“完美数对”，则 $3 (3 a + b) - (a + b - 2)$ 的值为（）

A、2 B、3 C、 $- 4$ D、 $- 6$

查看试题解析
3. 对于三个数a、b、c，P{a，b，c}表示这三个数的平均数，min{a，b，c}表示a、b、c这三个数中最小的数，max{a，b，c}表示这三个数中最大的数，例如：P{-1，2，3}＝ $\frac{- 1 + 2 + 3}{3} = \frac{4}{3}$ ， min{-1，2，3}＝-1，max{-2，-1，a}＝ ${\begin{array}{l} a (a > - 1) \\ - 1 (a < - 1) \end{array}$ .
下列判断：
①P ${- \sqrt{2} ， 0 ， \sqrt{18}} = 2 \sqrt{2}$ ；②max ${- 3 ， - \sqrt{5} ， - π} = - \sqrt{5}$ ；③若min{2，2x+2，4-2x}＝2，则0＜x＜1；④若P{2，x+1，2x}＝min{2，x+1，2x}，仅有唯一解x＝1；⑤max{x+1，（x-1）² ， 2-x}的最小值为 $\frac{3}{2}$ .其中正确的是（）

A、②③④⑤ B、①②④⑤ C、②③⑤ D、②④⑤

查看试题解析
4. 若 $1 0^{x} = N$ ，则称 $x$ 是以10为底 $N$ 的对数.记作： $x = l g N$ .例如： $1 0^{2} = 100$ ，则 $2 = l g 100$ ； $1 0^{0} = 1$ ，则 $0 = l g 1$ .对数运算满足：当 $M > 0$ ， $N > 0$ 时， $l g M + l g N = l g (M N)$ ，例如： $l g 3 + l g 5 = l g 15$ ，则 ${(l g 5)}^{2} + l g 5 \times l g 2 + l g 2$ 的值为（）

A、5 B、2 C、1 D、0

查看试题解析
5. 对多项式x-y-z-m-n任意加括号后仍然只含减法运算并将所得式子化简，称之为“加算操作”，例如：(x-y)-(z-m-n)=x-y-z+m+n，x-y-(z-m)-n = x-y-z+m-n，……，
给出下列说法：

①至少存在一种“加算操作”，使其结果与原多项式相等； ②不存在任何“加算操作”，使其结果与原多项式之和为0； ③所有的“加算操作”共有 8 种不同的结果．以上说法中正确的个数为（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

6. 华罗庚说过：“复杂的问题要善于‘退’，足够地‘退’，‘退’到最原始而不失重要性的地方，是学好数学的一个诀窍．”可见，复杂的问题有时要“退”到本质上去研究．如图，已知抛物线 $y = - x^{2} + 2 x - 1$ 的图象与f的图象关于直线 $y = x$ 对称，我们把探索线的变化规律“退”到探索点的变化规律上去研究，可以得到图象f所对应的关于x与y的关系式为 $x = - y^{2} + 2 y - 1$ ．若抛物线 $y = - x^{2} + 2 x - 1$ 与g的图象关于 $y = - x$ 对称，则图象g所对应的关于x与y的关系式为．

查看试题解析
7. 我们根据指数运算，得出了一种新的运算，如表是两种运算对应关系的一组实例：
指数运算
$2^{1} = 2$
$2^{2} = 4$
$2^{3} = 8$
$\dots$
$3^{1} = 3$
$3^{2} = 9$
$3^{3} = 27$
$\dots$
新运算
$l o g_{2} 2 = 1$
$l o g_{2} 4 = 2$
$l o g_{2} 8 = 3$
$\dots$
$l o g_{3} 3 = 1$
$l o g_{3} 9 = 2$
$l o g_{3} 27 = 3$
$\dots$
根据上表规律，某同学写出了三个式子：① $l o g_{2} 16 = 4$ ， ② $l o g_{5} 25 = 5$ ， ③ $l o g_{2} \frac{1}{2} = - 1$ ．
其中正确的是．

查看试题解析
8. 若a是不为2的有理数我们把 $\frac{2}{2 - a}$ 称为a的“哈利数”．如3的“哈利数”是 $\frac{2}{2 - 3} = - 2$ ； $- 2$ 的“哈利数”是 $\frac{2}{2 - (- 2)} = \frac{1}{2}$ ，已知 $a_{1} = 3$ ， $a_{2}$ 是 $a_{1}$ 的“哈利数”， $a_{3}$ 是 $a_{2}$ 的“哈利数”， $a_{4}$ 是 $a_{3}$ 的“哈利数”，以此类推， $a_{2023} =$ ．

查看试题解析
9. 对数的定义：一般地，若 $a^{x} = N$ （ $a > 0$ 且 $a \neq 1$ ），那么 $x$ 叫做以 $a$ 为底 $N$ 的对数，记作 $x = l o g_{a} N$ ，比如指数式 $2^{3} = 8$ 可以转化为对数式 $3 = l o g_{2} 8$ ，对数式 $2 = l o g_{6} 36$ ，可以转化为指数式 $6^{2} = 36$ ．计算 $l o g_{3} 9 + l o g_{5} 125 - l o g_{2} 32 =$ ．

查看试题解析
10. 平面直角坐标系中，若点P的坐标为 $(x ， y)$ ，点Q的坐标为 $(m x + y ， x + m y)$ ，其中m为常数，则称点Q是点P的m级派生点，例如点 $P (1 ， 2)$ 的3级派生点是 $(3 \times 1 + 2 ， 1 + 3 \times 2)$ ，即 $Q (5 ， 7)$ ．如图点 $Q (3 ， - 1)$ 是点 $P (x ， y)$ 的 $- 3$ 级派生点，点A在x轴上，且 $S_{△ A P Q} = 3$ ，则点A的坐标为．

查看试题解析
11. 我们规定：使得 $a - b = a b$ 成立的一对数a，b为“差积等数对”，记为 $(a ， b)$ ．例如，因为 $3 - 0.75 = 3 \times 0.75$ ， $(- 2) - 2 ＝ (- 2) \times 2$ ，所以数对 $(3 ， 0.75)$ ， $(- 2 ， 2)$ 都是“差积等数对”，若 $(k ， - 1)$ 是“差积等数对”，则k的值是．

查看试题解析
12. 我们知道四边形具有不稳定性，容易变形（给定四边形各边的长，其形状和大小不确定）．如图，一个矩形发生变形后成为一个平行四边形，设这个平行四边形中较小的内角为 $α$ ，我们把 $s i n α$ 的值叫做这个平行四边形的“变形系数”．如果矩形的面积为 $5$ ，其变形后的平行四边形的面积为 $4$ ，那么这个平行四边形的“变形系数”是．

查看试题解析
13. 定义：在平面直角坐标系 $x O y$ 中，O为坐标原点，对于任意两点 $P (x_{1} ， y_{1})$ 、 $Q (x_{2} ， y_{2})$ 称 $| x_{1} - x_{2} | + | y_{1} - y_{2} |$ 的值为P、Q两点的“直角距离”．直线 $y = - x + 5$ 与坐标轴交于A、B两点，Q为线段 $A B$ 上与点A、B不重合的一点，那么O、Q两点的“直角距离”是．

查看试题解析

三、综合题

14. 定义：对于一个三位正整数，如果十位数字恰好等于百位数字与个位数字之和的一半，我们称这个三位正整数为“半和数”．
例如，三位正整数234，因为 $3 = \frac{1}{2} \times (2 + 4)$ ，所以234是“半和数”．

(1)、判断147是否为“半和数”，并说明理由；

(2)、小林列举了几个“半和数”：111、123、234、840…，并且她发现： $111 \div 3 = 37$ ， $123 \div 3 = 41$ ， $234 \div 3 = 78$ ， $840 \div 3 = 280$ …，所以她猜测任意一个“半和数”都能被3整除．小林的猜想正确吗？若正确，请你帮小林说明该猜想的正确性；若错误，说明理由．

查看试题解析
15. 对于某些三角形，我们可以直接用面积公式或是用割补法等来求它们的面积，下面我们研究一种求面积的新方法：如图1所示，分别过三角形的顶点A、C作水平线的铅垂线 $l_{1}$ 、 $l_{2}$ ， $l_{1}$ 、 $l_{2}$ 之间的距离d叫做水平宽；如图1所示，过点B作水平线的铅垂线交 $A C$ 于点D，称线段 $B D$ 的长叫做这个三角形的铅垂高；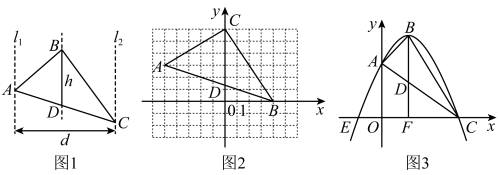
结论提炼：容易证明，“三角形的面积等于水平宽与铅垂高乘积的一半”，即“ $S = \frac{1}{2} d h$ ”．
尝试应用：

(1)、已知：如图2，点 $A (- 5 ， 3)$ 、 $B (4 ， 0)$ 、 $C (0 ， 6)$ ，则 $△ A B C$ 的水平宽为，铅垂高为，所以 $△ A B C$ 的面积为．

(2)、如图3，在平面直角坐标系中，抛物线的解析式为： $y = - x^{2} + 2 x + 3$ ，点B为抛物线的顶点，图象与y轴交于点A，与x轴交于E、C两点， $B D$ 为 $△ A B C$ 的铅垂高，延长 $B D$ 交x轴于点F，则顶点B坐标为，铅垂高 $B D =$ ， $△ A B C$ 的面积为．

查看试题解析
16. 定义：若一个函数图象上存在横、纵坐标相等的点，则称该点为这个函数图象的“等值点”，例如：点 $(1 ， 1)$ 是函数 $y = \frac{1}{2} x + \frac{1}{2}$ 的图像的“等值点”.

(1)、分别判断函数 $y = x + 1$ ， $y = x^{2} - x$ 的图像上是否存在“等值点”？如果存在，求出“等值点”的坐标；如果不存在，说明理由；

(2)、设函数 $y = \frac{3}{x} (x > 0)$ ， $y = - x + b$ 的图像的“等值点”分别为点 $A$ ， $B$ ，过点 $B$ 作 $B C ⊥ x$ 轴，垂足为 $C$ .当 $△ A B C$ 的面积为3时，求 $b$ 的值；

(3)、若函数 $y = x^{2} - 2 (x \geq m)$ 的图像记为 $W_{1}$ ，将其沿直线 $x = m$ 翻折后的图像记为 $W_{2}$ ，当 $W_{1}$ ， $W_{2}$ 两部分组成的图像上恰有2个“等值点”时，直接写出 $m$ 的取值范围.

查看试题解析
17. 【材料阅读】在等腰三角形中，我们把底边与腰长的比叫做顶角的张率(scop)．如图11-1，在△XYZ中，XY＝XZ，顶角X的张率记作 $s c o p ∠ X = \frac{底边}{腰} = \frac{Y Z}{X Y}$ ，容易知道一个角的大小与这个角的张率也是相互唯一确定的，所以，类比三角函数，我们可按上述方式定义∠α(0°<∠α<180°)的张率，例如，scop60°＝1，scop90°＝ $\sqrt{2}$ ，请根据材料，完成以下问题：
如图11-2，P是线段AB上的一动点(不与点A，B重合)，点C，D分别是线段AP，BP的中点，以AC，CD，DB为边分别在AB的同侧作等边三角形△ACE，△CDF，△DBG，连接PE和PG.

(1)、【理解应用】①若等边三角形△ACE，△CDF，△DBG的边长分别为a，b，c，则a，b，c三者之间的关系为；②scop∠EPG＝；

(2)、【猜想证明】如图11-3，连接EF，FG，猜想scop∠EFG的值是多少，并说明理由；

(3)、【拓展延伸】如图11-4，连接EF，EG，若AB＝12，EF= $2 \sqrt{7}$ ，则△EPG的周长是多少？此时AP的长为多少？（可直接写出上述两个结果），

查看试题解析
18. 阅读下列材料，按要求解答问题：
阅读理解：若p、q、m为整数，且三次方程 $x^{3} + p x^{2} + q x + m = 0$ 有整数解c，则将c代入方程得： $c^{3} + p c^{2} + q c + m = 0$ ，移项得： $m = - c^{3} - p c^{2} - q c$ ，即有： $m = c \times (- c^{2} - p c - q)$ ，由于 $- c^{2} - p c - q$ 与c及m都是整数，所以c是m的因数．
上述过程说明：整数系数方程 $x^{3} + p x^{2} + q x + m = 0$ 的整数解只可能是m的因数．
例如：方程 $x^{3} + 4 x^{2} + 3 x - 2 = 0$ 中－2的因数为±1和±2，将它们分别代入方程 $x^{3} + 4 x^{2} + 3 x - 2 = 0$ 进行验证得：x=－2是该方程的整数解，－1、1、2不是方程的整数解．
解决问题：
①根据上面的学习，请你确定方程 $x^{3} + x^{2} + 5 x + 7 = 0$ 的整数解只可能是哪几个整数？
②方程 $x^{3} - 2 x^{2} - 4 x + 3 = 0$ 是否有整数解？若有，请求出其整数解；若没有，请说明理由.

查看试题解析
19. 阅读以下材料：指数与对数之间有密切的联系，它们之间可以互化.
对数的定义：一般地，若 $a^{x} = N$ （ $a > 0$ 且 $a \neq 1$ ），那么x叫做以a为底N的对数，记作 $x = l o g_{a} N$ ，比如指数式 $2^{4} = 16$ 可以转化为对数式 $4 = l o g_{2} 16$ ，对数式 $2 = l o g_{5} 25$ ，可以转化为指数式 $5^{2} = 25$ .
我们根据对数的定义可得到对数的一个性质：
$l o g_{a} （ M \cdot N ） = l o g_{a} M + l o g_{a} N$ （ $a > 0$ ， $a \neq 1$ ， $M > 0$ ， $N > 0$ ），理由如下：
设 $l o g_{a} M = m$ ， $l o g_{a} N = n$ ，则 $M = a^{m}$ ， $N = a^{n}$ ，
$∴ M \cdot N = a^{m} \cdot a^{n} = {a^{m}}^{+ n}$ ，由对数的定义得 $m + n = l o g_{a} (M \cdot N)$
又 $∵ m + n = l o g_{a} M + l o g_{a} N$ ，
$∴ l o g_{a} (M \cdot N) = l o g_{a} M + l o g_{a} N$ .
请解决以下问题：

(1)、将指数式 $3^{4} = 81$ 转化为对数式；

(2)、求证： $l o g_{a} \frac{M}{N} = l o g_{a} M - l o g_{a} N$ （ $a > 0$ ， $a \neq 1$ ， $M > 0$ ， $N > 0$ ）；

(3)、拓展运用：计算 $l o g_{6} 9 + l o g_{6} 8 - l o g_{6} 2 =$ .

查看试题解析
20. 在平面直角坐标系中， $P (a ， b)$ 是第一象限内一点，给出如下定义： $k_{1} = \frac{a}{b}$ 和 $k_{2} = \frac{b}{a}$ 两个值中的最大值叫做点P的“倾斜系数”k．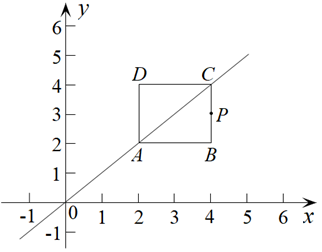

(1)、求点 $P (6 ， 2)$ 的“倾斜系数”k的值；

(2)、①若点 $P (a ， b)$ 的“倾斜系数” $k = 2$ ，请写出a和b的数量关系，并说明理由；
②若点 $P (a ， b)$ 的“倾斜系数” $k = 2$ ，且 $a + b = 3$ ，求OP的长；

(3)、如图，边长为2的正方形ABCD沿直线AC： $y = x$ 运动， $P (a ， b)$ 是正方形ABCD上任意一点，且点P的“倾斜系数” $k < \sqrt{3}$ ，请直接写出a的取值范围．

查看试题解析
21. 对于一个各数位上的数字均不为 0 的三位自然数 N，若 N 能被它的各数位上的数字之和 m 整除，则称 N 是 m 的“和倍数”．
例如：∵247÷(2+4+7)= 247÷13=19，∴247是13的“和倍数”.

又如： ∵214÷(2+1+4)=214÷7=30……4，∴214不是“和倍数”.

(1)、判断 357，441 是否是“和倍数”？说明理由；

(2)、三位数 A是12的“和倍数”，a，b，c 分别是数 A其中一个数位上的数字，且 a>b>c在 a，b，c 中任选两个组成两位数，其中最大的两位数记为 F (A)，最小的两位数记为 G(A)，若 $\frac{F (A) + G (A)}{16}$ 为整数，求出满足条件的所有数 A．

查看试题解析
22. 【问题】探究一次函数y＝kx+k+1（k≠0）图象特点．
【探究】可做如下尝试：
y＝kx+k+1＝k（x+1）+1，当x＝﹣1时，可以消去k，求出y＝1．
【发现】结合一次函数图象，发现无论k取何值，一次函数y＝kx+k+1的图象一定经过一个固定的点，该点的坐标是 ▲ ；
【应用】一次函数y＝（k+2）x+k的图象经过定点P．
①点P的坐标是 ▲ ；
②已知一次函数y＝（k+2）x+k的图象与y轴相交于点A，若△OAP的面积为3，求k的值．

查看试题解析
23. 数学教育家波利亚曾说：“对一个数学问题，改变它的形式，变换它的结构，直到发现有价值的东西，这是数学解题的一个重要原则”.
材料一：把根式 $\sqrt{x \pm 2 \sqrt{y}}$ 进行化简，若能找到两个数m、n，是 $m^{2} + n^{2} = x$ 且 $m n = \sqrt{y}$ ，则把 $x \pm 2 \sqrt{y}$ 变成 $m^{2} + n^{2} \pm 2 m n = {(m \pm n)}^{2}$ ，开方，从而使得 $\sqrt{x \pm 2 \sqrt{y}}$ 化简.

例如：化简 $\sqrt{3 + 2 \sqrt{2}}$

解：∵ $3 + 2 \sqrt{2} = 1 + 2 + 2 \sqrt{2} = 1^{2} + {(\sqrt{2})}^{2} + 2 \times 1 \times \sqrt{2} = {(1 + \sqrt{2})}^{2}$

∴ $\sqrt{3 + 2 \sqrt{2}} = \sqrt{{(1 + \sqrt{2})}^{2}} = 1 + \sqrt{2}$

材料二：在直角坐标系xOy中，对于点P（x，y）和Q（x，y'）给出如下定义：若 $y' = {\begin{array}{l} y ， (x \geq 0) \\ - y ， (x < 0) \end{array}$ ，则称Q点为P点的“横负纵变点”.例如点（3，2）的“横负纵变点”为（3，2），点（ $- 2$ ，5）的“横负纵变点”为（ $- 2$ ， $- 5$ ）.

请选择合适的材料解决下面的问题：

(1)、点（ $\sqrt{2}$ ， $- \sqrt{3}$ ）的“横负纵变点”为；

(2)、化简： $\sqrt{7 + 2 \sqrt{10}}$ ；

(3)、已知a为常数（ $1 \leq a \leq 2$ ），点M（ $- \sqrt{2}$ ，m）且 $m = \frac{1}{\sqrt{2}} (\sqrt{a + 2 \sqrt{a - 1}} + \sqrt{a - 2 \sqrt{a - 1}})$ ，点M'是点M的“横负纵变点”，求点M'的坐标.

查看试题解析

指数运算	$2^{1} = 2$	$2^{2} = 4$	$2^{3} = 8$	$\dots$	$3^{1} = 3$	$3^{2} = 9$	$3^{3} = 27$	$\dots$
新运算	$l o g_{2} 2 = 1$	$l o g_{2} 4 = 2$	$l o g_{2} 8 = 3$	$\dots$	$l o g_{3} 3 = 1$	$l o g_{3} 9 = 2$	$l o g_{3} 27 = 3$	$\dots$