浙江省绍兴市诸暨市2023届高三下学期5月数学联考试卷
试卷更新日期:2023-05-19 类型:高考模拟
一、单选题
-
1. 已知集合M={x|0≤x<2},N={x|x2-2x-3<0},则M∩N=( )A、{x|0≤x<1} B、{x|0≤x<2} C、{x|0≤x≤1} D、{x|0≤x≤2}2. 复数z1=3+i,z2=1-i,则z=z1·z2在复平面内的对应点位于( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知函数在区间内恰有一个极值,则的取值范围是( )A、 B、 C、 D、4. 马剑馒头在我市很有名,吃起来松软有韧劲,特别受欢迎.某马剑镇馒头商家为了将马剑馒头销往全国,学习了“小罐茶”的销售经验,决定走少而精的售卖方式,争取让马剑馒头走上高端路线,定制了如图所示由底面圆半径为的圆柱体和球冠(球的一部分,球心与圆柱底面圆心重合)组成的单独包装盒(包装盒总高度为5cm),请你帮忙计算包装盒的表面积( )(单位:平方厘米,球冠的表面积公式为 , 其中R为球冠对应球体的半径,h为球冠的高) A、 B、 C、 D、5. 已知点分别为直线上的动点,若 , 则的最小值为( )A、 B、 C、 D、6. 如图是函数的导函数的图象,若 , 则的图象大致为( )
A、 B、 C、 D、5. 已知点分别为直线上的动点,若 , 则的最小值为( )A、 B、 C、 D、6. 如图是函数的导函数的图象,若 , 则的图象大致为( )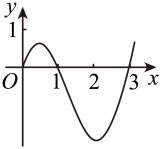 A、
A、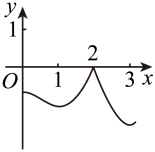 B、
B、 C、
C、 D、
D、 7. 已知圆 , 圆心为的圆分别与圆相切.圆的公切线(倾斜角为钝角)交圆于两点,则线段的长度为( )A、 B、 C、3 D、68. 定义域为的函数满足 , 且对于任意均有 , 则( )A、 B、 C、 D、
7. 已知圆 , 圆心为的圆分别与圆相切.圆的公切线(倾斜角为钝角)交圆于两点,则线段的长度为( )A、 B、 C、3 D、68. 定义域为的函数满足 , 且对于任意均有 , 则( )A、 B、 C、 D、二、多选题
-
9. 预测人口的变化趋势有多种方法,“直接推算法”使用的公式是 , 其中为预测期人口数,为初期人口数,为预测期内人口年增长率,为预测期间隔年数,则( )A、当 , 则这期间人口数呈下降趋势 B、当 , 则这期间人口数呈摆动变化 C、当时,的最小值为3 D、当时,的最小值为310. 一个袋子中有编号分别为的4个球,除编号外没有其它差异.每次摸球后放回,从中任意摸球两次,每次摸出一个球.设“第一次摸到的球的编号为2”为事件 , “第二次摸到的球的编号为奇数”为事件 , “两次摸到的球的编号之和能被3整除”为事件 , 则下列说法正确的是( )A、 B、事件与事件相互独立 C、 D、事件与事件互为对立事件11. 已知函数 , 下列说法正确的有( )A、若与图象至多有2个公共点 B、若与图象至少有2个公共点 C、若与图象至多有2个公共点 D、若与图象至少有2个公共点12. 过双曲线的左焦点的直线交的左、右支分别于两点,交直线于点 , 若 , 则( )A、 B、 C、 D、
三、填空题
-
13. 过点作曲线的切线,写出一条切线方程:.14. 已知椭圆的左顶点为 , 上顶点为为坐标原点,椭圆上的点分别在第一、二象限内,若与的面积相等,且 , 则的离心率为.15. 已知 , 则的展开式中,含项的系数的最大值为.16. 正方体的棱长为分别为上的点, , 分别为上的动点.若点在同一球面上,当平面时,该球的表面积为.
四、解答题
-
17. 记的内角的对边分别为 , 已知.(1)、若 , 求;(2)、若 , 求的面积.18. 如图,正三棱柱的所有棱长均为为的中点,为上一点,
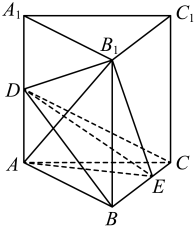 (1)、若 , 证明:平面;(2)、当直线与平面所成角的正弦值为 , 求的长度.19. 某同学进行投篮训练,已知该同学每次投中的概率均为0.5.
(1)、若 , 证明:平面;(2)、当直线与平面所成角的正弦值为 , 求的长度.19. 某同学进行投篮训练,已知该同学每次投中的概率均为0.5.附:若表示投篮的次数,表示投中的次数,则投中的频率为;若 , 则.
(1)、若该同学进行三次投篮,第一次投中得1分,第二次投中得1分,第三次投中得2分,记为三次总得分,求的分布列及数学期望;(2)、已知当随机变量服从二项分布时,若充分大,则随机变量服从标准正态分布.若保证投中的频率在0.4与0.6之间的概率不低于 , 求该同学至少要投多少次.