浙江省绍兴市上虞区2023届高三数学第二次适应性考试(二模)试卷
试卷更新日期:2023-05-19 类型:高考模拟
一、单选题
-
1. 已知集合 , 则( )A、 B、 C、 D、2. 已知复数满足 , 其中为虚数单位,则的虚部为( )A、 B、 C、 D、3. 在中, , 则在上的投影向量的模为( )A、1 B、2 C、 D、4. 已知函数在区间内取得一个最大值和一个最小值 , 且 , 则( )A、 B、 C、 D、5. 牟合方盖是由我国古代数学家刘徽发现并采用的,一种用于计算球体体积的方法,类似于现在的微元法.由于其采用的模型像一个牟合的方形盒子,故称为牟合方盖.本质上来说,牟合方盖是两个半径相等并且轴心互相垂直的圆柱体相交而成的三维图形,如图1所示.刘徽发现牟合方盖后200多年,祖冲之及他的儿子祖暅,推导出牟合方盖八分之一部分的体积计算公式为(为构成牟合方盖的圆柱底面半径).图2为某牟合方盖的部分,且图2正方体的棱长为1,则该牟合方盖的体积为( )
 A、 B、 C、 D、6. 已知直线与圆交于两点,若 , 其中为原点,则实数的值为( )A、1 B、 C、 D、27. 已知正数满足为自然对数的底数,则下列不等式一定成立的是( )A、 B、 C、 D、8. 如图,为直角梯形,.连 , 将沿翻折成三棱锥 , 当三棱锥外接球表面积的最小值时,二面角的余弦值为( )
A、 B、 C、 D、6. 已知直线与圆交于两点,若 , 其中为原点,则实数的值为( )A、1 B、 C、 D、27. 已知正数满足为自然对数的底数,则下列不等式一定成立的是( )A、 B、 C、 D、8. 如图,为直角梯形,.连 , 将沿翻折成三棱锥 , 当三棱锥外接球表面积的最小值时,二面角的余弦值为( )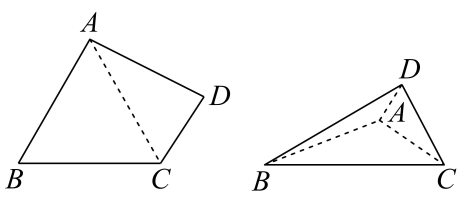 A、 B、0 C、 D、
A、 B、0 C、 D、二、多选题
-
9. 记正项等比数列的前n项和为 , 则下列数列为等比数列的有( )A、 B、 C、 D、10. 某学校一同学研究温差与本校当天新增感冒人数(人)的关系,该同学记录了5天的数据:
5
6
8
9
12
17
20
25
28
35
经过拟合,发现基本符合经验回归方程 , 则( )
A、样本中心点为 B、 C、时,残差为 D、若去掉样本点 , 则样本的相关系数增大11. 声音是由物体振动产生的声波,纯音的数学模型是函数 , 我们听到的声音是由纯音合成的,称之为复合音.我们听到的声音函数是 , 记 , 则下列结论中正确的为( )A、在上是增函数 B、的最大值为 C、的最小正周期为 D、12. 已知点是椭圆的左右焦点,点为椭圆上一点,点关于平分线的对称点也在椭圆上,若 , 则( )A、的周长为 B、 C、平分线的斜率为 D、椭圆的离心率为三、填空题
-
13. 设双曲线的两条渐近线互相垂直,则此双曲线的离心率为.14. 已知的展开式的常数项是第7项,则.15. 已知函数为偶函数,且 , 则.16. 已知函数 , 若在区间上有零点,则的最大值为.
四、解答题
-
17. 设数列的前项和为 , 数列是首项为1,公差为1的等差数列,(1)、求数列的通项公式;(2)、设 , 求数列的前项和.18. 如图,在多面体中,平面为正三角形,为等腰Rt.
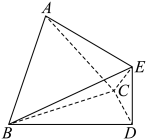 (1)、求证:;(2)、若平面 , 求直线与平面所成的线面角的正弦值.19. 在中,内角所对的边分别为 , 且.(1)、求的值;(2)、求的最大值.20. 某手机APP公司对喜欢使用该APP的用户年龄情况进行调查,随机抽取了100名喜欢使用该APP的用户,年龄均在周岁内,按照年龄分组得到如下所示的样本频率分布直方图:
(1)、求证:;(2)、若平面 , 求直线与平面所成的线面角的正弦值.19. 在中,内角所对的边分别为 , 且.(1)、求的值;(2)、求的最大值.20. 某手机APP公司对喜欢使用该APP的用户年龄情况进行调查,随机抽取了100名喜欢使用该APP的用户,年龄均在周岁内,按照年龄分组得到如下所示的样本频率分布直方图: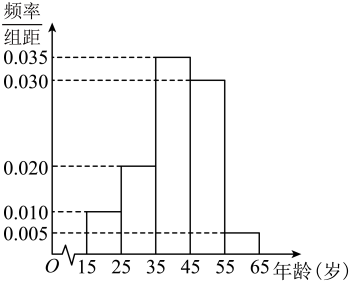
附:若随机变量服从正态分布 , 则:
(1)、根据频率分布直方图,估计使用该视频APP用户的平均年龄的第分位数(小数点后保留2位);(2)、若所有用户年龄近似服从正态分布 , 其中为样本平均数的估计值, , 试估计喜欢使用该APP且年龄大于61周岁的人数占所有喜欢使用该APP的比例;(3)、用样本的频率估计概率,从所有喜欢使用该APP的用户中随机抽取8名用户,用表示这8名用户中恰有名用户的年龄在区间岁的概率,求取最大值时对应的的值;