浙江省绍兴市柯桥区2023届高三5月高考数学及选考科目适应性考试试卷
试卷更新日期:2023-05-19 类型:高考模拟
一、单选题
-
1. 若集合 , , 则( )A、 B、 C、 D、2. 在中, , , 设 , , 则( )A、 B、 C、 D、3. 欧拉公式(i为虚数单位)是由瑞士著名数学家欧拉创立,依据欧拉公式,下列选项不正确的是( )A、复数的虚部为 B、若 , 则复数对应点位于第二象限 C、复数的模长等于1 D、复数的共轭复数为4. “曲池”是《九章算术》记载的一种几何体,该几何体是上、下底面均为扇环形的柱体(扇环是指圆环被扇形截得的部分).现有一个如图所示的曲池,面ABCD, , 底面扇环所对的圆心角为 , 的长度是长度的2倍, , 则异面直线与所成角的正弦值为( )
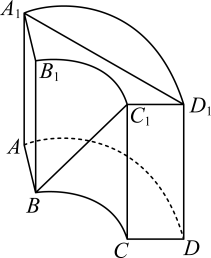 A、 B、 C、 D、5. 6名同学参加数学和物理两项竞赛,每项竞赛至少有1名同学参加,每名同学限报其中一项,则两项竞赛参加人数相等的概率为( )A、 B、 C、 D、6. 若函数的周期为 , 其图象由函数的图象向左平移个单位得到,则的一个单调递增区间是( )A、 B、 C、 D、7. 已知 , , , 则( )A、 B、 C、 D、8. 如图,平面四边形ABCD中, , 为正三角形,以AC为折痕将折起,使D点达到P点位置,且二面角的余弦值为 , 当三棱锥的体积取得最大值,且最大值为时,三棱锥外接球的体积为( )
A、 B、 C、 D、5. 6名同学参加数学和物理两项竞赛,每项竞赛至少有1名同学参加,每名同学限报其中一项,则两项竞赛参加人数相等的概率为( )A、 B、 C、 D、6. 若函数的周期为 , 其图象由函数的图象向左平移个单位得到,则的一个单调递增区间是( )A、 B、 C、 D、7. 已知 , , , 则( )A、 B、 C、 D、8. 如图,平面四边形ABCD中, , 为正三角形,以AC为折痕将折起,使D点达到P点位置,且二面角的余弦值为 , 当三棱锥的体积取得最大值,且最大值为时,三棱锥外接球的体积为( )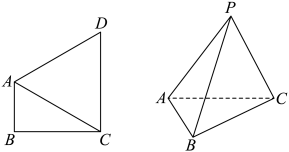 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 设随机变量 , 随机变量 , 则( )A、 B、 , C、 D、10. 已知正n边形的边长为a,内切圆的半径为r,外接圆的半径为R,则( )A、当时, B、当时, C、 D、11. 已知、分别是双曲线的左、右焦点,过点作双曲线的切线交双曲线于点(在第一象限),点在延长线上,则下列说法正确的是( )A、 B、 C、为的平分线 D、的角平分线所在直线的倾斜角为12. 若函数为函数的导函数,且对于任意实数 , 均有 , 且 , 则( )A、函数不可能为奇函数 B、存在实数M,使得 C、存在实数N,使得 D、函数不存在零点
三、填空题
-
13. 现有如下10个数据:
296 301 305 293 293 305 302 303 306 294
则这批数据的第一四分位数为 .
14. 展开式中的系数为 .15. 若函数的图象不过第四象限,则实数a的取值范围为 .16. 函数的最大值为 .四、解答题
-
17. 已知数列 , 的前n项和分别为 , , 且 , , 当时,满足 .(1)、求;(2)、求 .18. 已知a,b,c分别为中三内角A,B,C的对边,且 , , D为直线BC上一动点.(1)、求A;(2)、在① , ② , ③这三个条件中任选一个,求线段AD长度的最小值.19. 如图,在四棱锥中,底面ABCD为平行四边形, , 侧面底面ABCD, , 且二面角的大小是 .
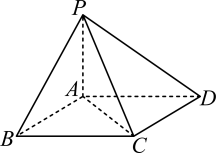 (1)、证明:;(2)、求二面角的正弦值.20. 如图,是一块高尔顿板的示意图,在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃,让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左或向右滚下,最后掉入编号为的球槽内.用X表示小球经过第7层通过的空隙编号(从左向右的空隙编号依次为),用Y表示小球最后落入球槽的号码.
(1)、证明:;(2)、求二面角的正弦值.20. 如图,是一块高尔顿板的示意图,在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃,让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左或向右滚下,最后掉入编号为的球槽内.用X表示小球经过第7层通过的空隙编号(从左向右的空隙编号依次为),用Y表示小球最后落入球槽的号码.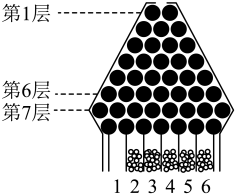 (1)、若进行一次高尔顿板试验,求小球落入第7层第3个空隙处的概率;(2)、若放入80个小球,求落入1号球槽的小球个数Z的均值与方差.
(1)、若进行一次高尔顿板试验,求小球落入第7层第3个空隙处的概率;(2)、若放入80个小球,求落入1号球槽的小球个数Z的均值与方差.