浙江省七彩阳光联盟2022-2023学年高一下学期期中数学试卷
试卷更新日期:2023-05-19 类型:期中考试
一、单选题
-
1. 已知集合 , 则( )A、 B、 C、 D、2. 若 , 则( )A、32 B、16 C、4 D、23. 在中,“”是“”的( )条件A、充分不必要 B、必要不充分 C、充要 D、既不充分也不必要4. 如图所示,F为平行四边形对角线BD上一点, , 则( )
 A、 B、 C、 D、5. 已知 , 则的值等于( )A、 B、 C、 D、6. 已知向量 , 向量在方向上的投影向量为( )A、 B、 C、 D、7. 如图扇形 , 圆心角 , D为半径中点,把扇形分成三部分,这三部分绕AC旋转一周,所得三部分旋转体的体积之比是( )
A、 B、 C、 D、5. 已知 , 则的值等于( )A、 B、 C、 D、6. 已知向量 , 向量在方向上的投影向量为( )A、 B、 C、 D、7. 如图扇形 , 圆心角 , D为半径中点,把扇形分成三部分,这三部分绕AC旋转一周,所得三部分旋转体的体积之比是( )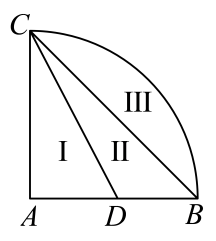 A、 B、 C、 D、8. 已知平面向量 , 且的最小值与的最小值乘积为2(为实数),则的最小值为( )A、1 B、 C、2 D、
A、 B、 C、 D、8. 已知平面向量 , 且的最小值与的最小值乘积为2(为实数),则的最小值为( )A、1 B、 C、2 D、二、多选题
-
9. 已知函数 , 则下列判断错误的是( )A、是奇函数 B、的图像与直线有两个交点 C、的值域是 D、在区间上是减函数10. 已知函数的部分图像如图所示,则下列关于函数的说法正确的是( )
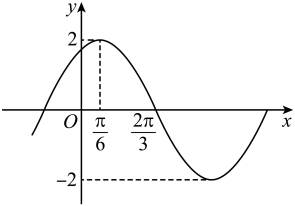 A、 B、函数的绝对值最小的零点为 C、直线是函数的一条对称轴 D、函数在上单调递增11. 如图在棱长为6的正方体中,分别是中点,P在侧面上(包括边界),且满足三棱锥的体积等于9,则的长度可以是( )
A、 B、函数的绝对值最小的零点为 C、直线是函数的一条对称轴 D、函数在上单调递增11. 如图在棱长为6的正方体中,分别是中点,P在侧面上(包括边界),且满足三棱锥的体积等于9,则的长度可以是( )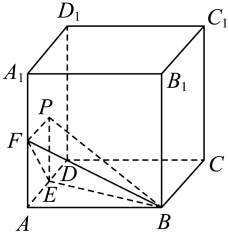 A、 B、 C、10 D、12. 无字证明来源于《几何原本》第二卷的几何代数法(用几何方法研究代数问题),很多代数的公式或定理都能仅通过图形得以证明、如图,在中,为BC边上异于端点的两点, , 且是边长为b的正三角形,则下列不等式一定成立的是( )
A、 B、 C、10 D、12. 无字证明来源于《几何原本》第二卷的几何代数法(用几何方法研究代数问题),很多代数的公式或定理都能仅通过图形得以证明、如图,在中,为BC边上异于端点的两点, , 且是边长为b的正三角形,则下列不等式一定成立的是( )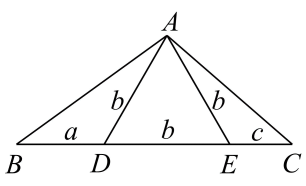 A、 B、 C、 D、
A、 B、 C、 D、三、填空题
-
13. 函数的零点是14. 已知复数(i为虚数单位),则z的虚部为.15. 平面直角坐标系xOy中线段OA的长为 , 与x轴所成的夹角为 , 且 , 在斜二测画法下 , 其直观图为线段 , 则线段的长度为 .
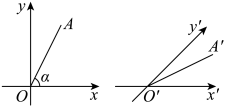 16. 已知的三个角所对的边为 , 若 , D为边BC上一点,且 , 则的值为 .
16. 已知的三个角所对的边为 , 若 , D为边BC上一点,且 , 则的值为 .四、解答题
-
17.(1)、已知 , 求的值;(2)、计算: .18. 已知复数(i为虚数单位)和是关于x的方程两根,(1)、求p和;(2)、若对应复平面内的点A,且是以A为直角顶点的等腰直角三角形,求点B对应的复数 .19. 如图,为了测量两山顶间的距离,飞机沿水平方向在两点进行测量,在同一个铅垂平面内,在A点测得的俯角分别为 , 在B点测得的俯角分别为 , 同时测得 .
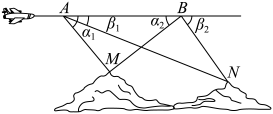 (1)、求BN和AM的长度;(2)、求之间的距离.
(1)、求BN和AM的长度;(2)、求之间的距离.