浙江省金华市义乌市2023届高三下学期数学适应性考试试卷
试卷更新日期:2023-05-19 类型:高考模拟
一、单选题
-
1. 已知集合 , 则( )A、 B、 C、 D、2. 若复数 , 则复数的模( )A、3 B、5 C、9 D、253. 双曲线的渐近线方程为( )A、 B、 C、 D、4. 学校举行德育知识竞赛,甲、乙、丙、丁、戊5位同学晋级到了决赛环节,通过笔试决出了第1名到第5名.甲、乙两名参赛者去询问成绩,回答者对他们说:“决赛5人的成绩各不相同,但你们俩的名次是相邻的”,丙、丁两名参赛者也去询问成绩,回答者对丙说:“很遗憾,你和丁都未拿到冠军”,又对丁说:“你当然不会是最差的”.从这个回答分析,5人的名次排列共有( )种不同的可能情况.A、14 B、16 C、18 D、205. 为了得到函数的图象,只要把图象上所有的点( )A、向右平行移动个单位长度 B、向左平行移动个单位长度 C、向右平行移动个单位长度 D、向左平行移动个单位长度6. 在中, , , 则( )A、 B、 C、 D、7. 在半径为的实心球中挖掉一个圆柱,再将该圆柱重新熔成一个球 , 则球的表面积的最大值为( )A、 B、 C、 D、8. 已知定义域为的函数满足 , 且在区间上还满足:①当时,都有;②;③.则等于( )A、 B、 C、1 D、
二、多选题
-
9. 下列说法正确的是( )A、若随机变量 , 则 B、样本相关系数的绝对值越接近 , 成对样本数据线性相关程度越强 C、数据的第百分位数为 D、抛掷一枚质地均匀的骰子所得的样本空间为 , 令事件 , , 则事件不独立10. 古希腊数学家欧几里得在《几何原本》卷11中这样定义棱柱:一个棱柱是一个立体图形,它是由一些平面构成的,其中有两个面是相对的、相等的,相似且平行的,其它各面都是平行四边形.显然这个定义是有缺陷的,由于《几何原本》作为“数学圣经”的巨大影响,该定义在后世可谓谬种流传,直到1916年,美国数学家斯顿(J.C.Stone)和米利斯(J.F.Millis)首次给出欧氏定义的反例.如图1,八面体的每一个面都是边长为2的正三角形,且4个顶点A,B,C,D在同一平面内,取各棱的中点,切割成欧氏反例(如图2),则该欧氏反例( )
 A、共有12个顶点 B、共有24条棱 C、表面积为 D、体积为11. 已知拋物线 , 点均在抛物线上,点 , 则( )A、直线的斜率可能为 B、线段长度的最小值为 C、若三点共线,则存在唯一的点 , 使得点为线段的中点 D、若三点共线,则存在两个不同的点 , 使得点为线段的中点12. 当且时,不等式恒成立,则自然数可能为( )A、0 B、2 C、8 D、12
A、共有12个顶点 B、共有24条棱 C、表面积为 D、体积为11. 已知拋物线 , 点均在抛物线上,点 , 则( )A、直线的斜率可能为 B、线段长度的最小值为 C、若三点共线,则存在唯一的点 , 使得点为线段的中点 D、若三点共线,则存在两个不同的点 , 使得点为线段的中点12. 当且时,不等式恒成立,则自然数可能为( )A、0 B、2 C、8 D、12三、填空题
-
13. 的展开式中的系数是.(用数字作答).14. 若 , 则.15. 若存在直线既是曲线的切线,也是曲线的切线,则实数的最大值为.16. 已知三点在圆上,的重心为坐标原点 , 则周长的最大值为.
四、解答题
-
17. 设正项等比数列的前项和为 , 若 , .(1)、求数列的通项公式;(2)、在数列中是否存在不同的三项构成等差数列?请说明理由.18. 为迎接“五一小长假”的到来,某商场开展一项促销活动,凡在商场消费金额满200元的顾客可以免费抽奖一次,抽奖规则如下:在不透明箱子中装有除颜色外其他都相同的10个小球,其中,红球2个,白球3个,黄球5个,顾客从箱子中依次不放回地摸出2个球,根据摸出球的颜色情况分别进行兑奖.将顾客摸出的2个球的颜色分成以下四种情况::1个红球1个白球,:2个红球,:2个白球,:至少一个黄球.若四种情况按发生的概率从小到大的顺序分别对应一等奖,二等奖,三等奖,不中奖.(1)、求顾客在某次抽奖中,第二个球摸到为红球的概率(2)、求顾客分别获一、二、三等奖时对应的概率;(3)、若三名顾客每人抽奖一次,且彼此是否中奖相互独立.记中奖的人数为 , 求的分布列和期望.19. 在四棱锥中,底面为梯形,为上的点,且.
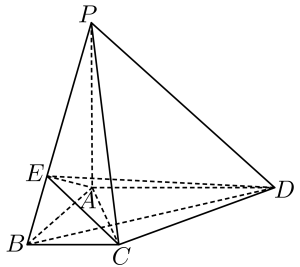 (1)、证明:面:(2)、若面 , 面面 , 求二面角的正弦值.
(1)、证明:面:(2)、若面 , 面面 , 求二面角的正弦值.