2022~2023学年浙教版数学八年级下学期期末模考数学试卷（四）

试卷更新日期：2023-05-18 类型：期末考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列方程属于一元二次方程的是（）

A、 $x^{2} - y + 2 = 0$ B、 $x^{2} + y^{2} = 1$ C、 $x^{2} - 2 x + 2 = 0$ D、 $x^{2} - \frac{1}{x} = 5$

查看试题解析
2. 方程：x²﹣25=0的解是（）

A、x=5 B、x=﹣5 C、x₁=﹣5，x₂=5 D、x=±25

查看试题解析
3. 估计 $(2 \sqrt{2} + 4 \sqrt{3}) \times \sqrt{\frac{1}{2}}$ 的值应在（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析
4. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念，全班共送1056张照片，如果全班有x名同学，根据题意，列出方程为（）

A、x（x+1）＝1056 B、x（x-1）＝1056×2 C、x（x-1）＝1056 D、2x（x+1）＝1056

查看试题解析
5. 如果一个三角形的其中两边长分别是方程 $x^{2} - 8 x + 15 = 0$ 的两个根，那么连结这个三角形三边的中点，得到的三角形的周长可能是（　　）

A、5.5 B、5 C、4.5 D、4

查看试题解析
6. 如图，在四边形ABCD中，∠A=37°，∠C=26°，∠D=50°，则∠1等于（）

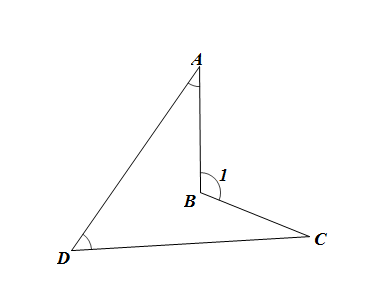A、87° B、100° C、113° D、247°

查看试题解析
7. 某商场为了解产品A的销售情况，在上个月的销售记录中，随机抽取了5天A产品的销售记录，其售价x（元/件）与对应销量y（件）的全部数据如下表：
售价x（元/件）
90
95
100
105
110
销量y（件）
110
100
80
60
50
则这5天中，A产品平均每件的售价为（）

A、100元 B、95元 C、98元 D、97.5元

查看试题解析
8. 如图，已经点 $A$ 在反比例函数 $y = \frac{k}{x} (x < 0)$ 上，点 $B$ ， $C$ 在 $x$ 轴上，使得 $∠ A B C = 90 °$ ，点 $D$ 在线段 $A C$ 上，且满足 $2 C D = 3 A D$ ，连接 $D B$ 并延长交 $y$ 轴于点 $E$ .若 $△ B C E$ 的面积为6，则 $k$ 的值为（）

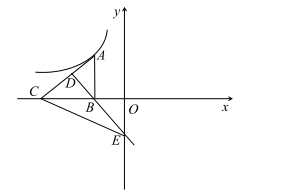A、-5 B、-6 C、-8 D、-7

查看试题解析
9.
如图，矩形ABCD的两条对角线相交于点O，∠AOD=60°，AD=2，则AC的长是（　　）

A、2 B、4 C、2 $\sqrt{3}$ D、4 $\sqrt{3}$

查看试题解析
10. 如图，三个边长均为4的正方形重叠在一起，O₁ ， O₂是其中左侧两个正方形的对角线交点，同时O₁ ， O₂也是右侧两个正方形的顶点，根据教材第63页《实践与探究》活动中有关内容，可知阴影部分面积是（　　　　）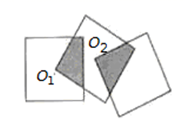

A、2 B、4 C、6 D、8

查看试题解析

二、填空题（每空4分，共24分）

11. 若2(x-1)²-8=0，则x的值为．

查看试题解析
12. $\sqrt{12}$ 与最简二次根式 $- 4 \sqrt{a + 1}$ 是同类二次根式，则a＝.

查看试题解析
13. 如图，AB∥CD，AD∥BC，EF过AC与BD的交点O.图中全等三角形有对

查看试题解析
14. 设甲组数： $1$ ， $1$ ， $2$ ， $5$ 的方差为 $S_{甲}^{2}$ ，乙组数是： $6$ ， $6$ ， $6$ ， $6$ 的方差为 $S_{乙}^{2}$ ，则 $S_{甲}^{2}$ 与 $S_{乙}^{2}$ 的大小关系是 $S_{甲}^{2}$ $S_{乙}^{2}$ （选择“>”、“<”或“=”填空）.

查看试题解析
15. 用4张全等的直角三角形纸片拼接成如图所示的图案，得到两个大小不同的正方形．若正方形ABCD的面积为10，AH＝3，则正方形EFGH的面积为．

查看试题解析
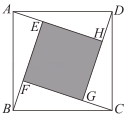16. 如图，将正方形纸板制成一个七巧板，拼成如图 $2$ 所示的“小鸟”图案，头部（阴影部分）的面积为 $18 c m^{2}$ ，则“小鸟”图案中身体（空白部分）的面积为．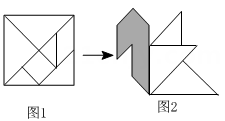

查看试题解析

三、解答题（第17题4分，第18题4分，第19题5分，第20题8分，第21题5分，第22题5分，第23题5分，第24题10分，共8题，共46分）

17. 解方程：

(1)、x²﹣2x﹣4＝0；

(2)、2x²﹣7x﹣4＝0．

查看试题解析
18. 计算：

(1)、 $2 \sqrt{12} - 6 \sqrt{\frac{1}{3}} + 3 \sqrt{48}$

(2)、 $(\sqrt{5} - 2) (2 + \sqrt{5}) - {(- \sqrt{3})}^{2} + \sqrt{8} \times \frac{1}{\sqrt{2}}$

查看试题解析
19.
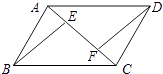
如图，E、F是平行四边形ABCD对角线AC上的两点，BE∥DF．求证：BE=DF．

查看试题解析
20. 入为响应习近平提出的“绿水青山就是金山银山”的重要思想某校举办了“绿水青山，生态文明”知识竞赛(竞每一项的满分10分，学生得分均为整数).在这次竞赛中张山与李仕两位同学表现优秀，他们的四项成绩分布的条形统计图如图所示根据上图结果解答下列问题。

(1)、补充完成下表
姓名
平均成绩(分)
中位数(分)
众数(分)
方差(分²)
张山
9

9

李仕

9.5

1.5

(2)、根据(1)题数据，分别从中位数、方差两个角度比较说明两位同学的各自优势?

(3)、若实践操作、环保论文、现场抢答、笔试得分技4：1：2：3的比例折合成综合得分，请通过计算说明哪位同学的综合得分更高。

查看试题解析
21. 某乡镇要在生活垃圾存放区建一个老年活动中心，这样必须把1200立方米的生活垃圾运走：
（1）假如每天能运x立方米，所需时间为y天，写出y与x之间的函数表达式；
（2）若每辆拖拉机一天能运12立方米，则5辆这样的拖拉机要用多少天才能运完？
（3）在（2）的情况下，运了8天后，剩下的任务要在不超过6天的时间内完成，那么至少需要增加多少辆这样的拖拉机才能按时完成任务？

查看试题解析
22. 今年春季某地区流感爆发，开始时有4人患了流感，经过两轮传染后，共有196人患了流感．若每轮每人传染的人数相同，求每轮每人传染的人数．

查看试题解析
23.
已知 $A (- 1 ， m)$ 与 $B (2 ， m + 3)$ 是反比例函数 $y = \frac{k}{x}$ 图象上的两个点.

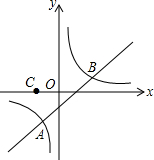
(1)求m和k的值
(2)若点C(-1，0)，连结AC，BC，求△ABC的面积
(3)根据图象直接写出一次函数的值大于反比例函数的值的 $x$ 的取值范围.

查看试题解析
24. 如图1，在Rt△ABC中，边AB，BC的长分别是3与4．点P从点A出发，以每秒1个单位的速度沿△ABC边A→B→C→A的方向运动，运动时间为t秒．

(1)、当点P运动到边BC上时，试求出使AP长为 $\sqrt{10}$ 时运动时间t的值；

(2)、如图2，以AC为边作△CDA，使△CDA≌△ABC，且点P运动到AC上．
①当DP⊥_AC时，求出运动时间t的值；

②是否存在点P ，使△CDP是以CD为腰的等腰三角形？若存在，请求出运动时间t的值；若不存在，请说明理由．

查看试题解析

售价x（元/件）	90	95	100	105	110
销量y（件）	110	100	80	60	50

姓名	平均成绩(分)	中位数(分)	众数(分)	方差(分²)
张山	9		9
李仕		9.5		1.5