湖北省孝感市2023年中考数学二模试卷
试卷更新日期:2023-05-18 类型:中考模拟
一、选择题(本大题共8小题,共24.0分。)
-
1. -3的绝对值是( )A、3 B、 C、 D、-32. 某种芯片每个探针单元的面积为 , 0.0000064用科学记数法表示为( )A、 B、 C、 D、3. “致中和,天地位焉,万物育焉.”中国古人把和谐平衡的精神之美,演变成了一种对称美,在下列我国建筑简图中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算结果正确的是( )A、 B、 C、 D、5. 如图,由8个大小相同的正方体搭成的几何体,其俯视图是( )
4. 下列运算结果正确的是( )A、 B、 C、 D、5. 如图,由8个大小相同的正方体搭成的几何体,其俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 下列说法正确的是( )A、“掷一枚硬币正面朝上的概率是”表示每抛硬币2次就有1次正面朝上 B、一组数据2,2,3,6的众数和中位数都是2 C、要了解全市人民的低碳生活状况,适宜采用抽样调查的方法 D、随机抽取甲、乙两名同学的5次数学成绩,计算得平均分都是90分,方差分别是 , , 说明乙的成绩较为稳定7. 如图,矩形的对角线经过坐标原点,矩形的边分别平行于坐标轴,点在反比例函数的图象上.若点的坐标为 , 则的值为( )
6. 下列说法正确的是( )A、“掷一枚硬币正面朝上的概率是”表示每抛硬币2次就有1次正面朝上 B、一组数据2,2,3,6的众数和中位数都是2 C、要了解全市人民的低碳生活状况,适宜采用抽样调查的方法 D、随机抽取甲、乙两名同学的5次数学成绩,计算得平均分都是90分,方差分别是 , , 说明乙的成绩较为稳定7. 如图,矩形的对角线经过坐标原点,矩形的边分别平行于坐标轴,点在反比例函数的图象上.若点的坐标为 , 则的值为( ) A、1 B、-1或3 C、4 D、1或-38. 在中, , , 正方形的边长为1,将正方形和如图放置,与在一条直线上,点与点重合.现将正方形沿方向以每秒1个单位的速度匀速运动,当点与点重合时停止.在这个运动过程中,正方形和重叠部分的面积与运动时间的函数图象大致是( )
A、1 B、-1或3 C、4 D、1或-38. 在中, , , 正方形的边长为1,将正方形和如图放置,与在一条直线上,点与点重合.现将正方形沿方向以每秒1个单位的速度匀速运动,当点与点重合时停止.在这个运动过程中,正方形和重叠部分的面积与运动时间的函数图象大致是( ) A、
A、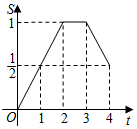 B、
B、 C、
C、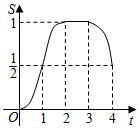 D、
D、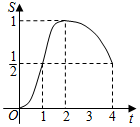
二、填空题(本大题共8小题,共24.0分)
-
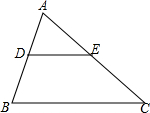
9. 分解因式: .10. 如图, , 若 , , , 则的长为 .
 11. 已知函数 , 点在函数图象上当时, .12. 如图,在中, , , 观察图中尺规作图的痕迹,则的度数为 .
11. 已知函数 , 点在函数图象上当时, .12. 如图,在中, , , 观察图中尺规作图的痕迹,则的度数为 .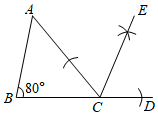 13. 如图,某一时刻在灯塔处观测到货轮在它的北偏东方向,同时又观测到客轮在它的东南方向,则的度数是 .
13. 如图,某一时刻在灯塔处观测到货轮在它的北偏东方向,同时又观测到客轮在它的东南方向,则的度数是 . 14. 某中学为了解初三学生的视力情况,对全体初三学生的视力进行了检测,将所得数据整理后画出频率分布直方图如图 , 已知图中从左到右第一、二、三、五小组的频率分别为0.05,0.1,0.25,0.1,如果第四小组的频数是180人,那么该校初三共有位学生.
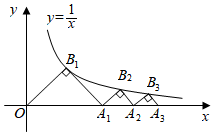
14. 某中学为了解初三学生的视力情况,对全体初三学生的视力进行了检测,将所得数据整理后画出频率分布直方图如图 , 已知图中从左到右第一、二、三、五小组的频率分别为0.05,0.1,0.25,0.1,如果第四小组的频数是180人,那么该校初三共有位学生. 15. 如图, , , …, 都是斜边在x轴上的等腰直角三角形,点 , , ,…, 都在x轴上,点 , , ,…, 都在反比例函数 的图象上,则点 的坐标为 . (用含有正整数n的式子表示)
15. 如图, , , …, 都是斜边在x轴上的等腰直角三角形,点 , , ,…, 都在x轴上,点 , , ,…, 都在反比例函数 的图象上,则点 的坐标为 . (用含有正整数n的式子表示)
 16. 如图,▱的顶点、在第二象限,点 , 反比例函数图象经过点和边的中点 , 若 , 则的值为用含的式子表示
16. 如图,▱的顶点、在第二象限,点 , 反比例函数图象经过点和边的中点 , 若 , 则的值为用含的式子表示
三、解答题(本大题共8小题,共72.0分。)
-
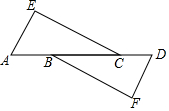
17. 计算: .18. 如图,点 , , , 在同一直线上, , , 求证: .
 19. “二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”小明购买了“二十四节气”主题邮票,他将“立春”“清明”“雨水”三张纪念邮票除正面内容不同外,其余均相同背面朝上,洗匀放好.
19. “二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”小明购买了“二十四节气”主题邮票,他将“立春”“清明”“雨水”三张纪念邮票除正面内容不同外,其余均相同背面朝上,洗匀放好. (1)、小明从中随机抽取一张邮票是“立春”的概率是 .(2)、小明从中随机抽取一张邮票,记下内容后,正面向下放回,洗匀后再从中随机抽取一张邮票请用画树状图或列表的方法,求小明两次抽取的邮票中至少有一张是“雨水”的概率这三张邮票依次分别用字母 , , 表示 .20. 如图,一次函数的图象与反比例函数在第一象限内的图象交于和两点.
(1)、小明从中随机抽取一张邮票是“立春”的概率是 .(2)、小明从中随机抽取一张邮票,记下内容后,正面向下放回,洗匀后再从中随机抽取一张邮票请用画树状图或列表的方法,求小明两次抽取的邮票中至少有一张是“雨水”的概率这三张邮票依次分别用字母 , , 表示 .20. 如图,一次函数的图象与反比例函数在第一象限内的图象交于和两点. (1)、求反比例函数的表达式.(2)、在第一象限内,当一次函数的值大于反比例函数的值时,写出自变量的取值范围.(3)、求面积.21. 如图,半圆O的直径 , 圆心为点O.点E在上,四边形是平行四边形,顶点C在半圆上, , 垂足为F,.
(1)、求反比例函数的表达式.(2)、在第一象限内,当一次函数的值大于反比例函数的值时,写出自变量的取值范围.(3)、求面积.21. 如图,半圆O的直径 , 圆心为点O.点E在上,四边形是平行四边形,顶点C在半圆上, , 垂足为F,. (1)、求证:是的切线;(2)、求的长及图中阴影部分的面积.22. 蔬菜基地种植某种蔬菜,由市场行情分析知,1月份至3月份这种蔬菜的上市时间月份与市场售价元千克的关系如表:
(1)、求证:是的切线;(2)、求的长及图中阴影部分的面积.22. 蔬菜基地种植某种蔬菜,由市场行情分析知,1月份至3月份这种蔬菜的上市时间月份与市场售价元千克的关系如表:上市时间月份
1
2
3
4
5
6
市场售价元千克
10.5
9
7.5
6
4.5
3
这种蔬菜每千克的种植成本元千克与上市时间月份满足一个函数关系,这个函数的图象是抛物线的一段如图 .
 (1)、写出表中表示的市场售价元千克关于上市时间月份的函数关系式;(2)、若图中抛物线过 , , 点,求出抛物线对应的函数关系式;(3)、由以上信息分析,几月份上市出售这种蔬菜每千克的收益最大,最大值为多少元(收益市场售价种植成本).23. 如图,在矩形 ABCD 中,E 为 BC 上一点,以 DE 为边作矩形 DEGF,其中GF 经过点 A,连接 AE.
(1)、写出表中表示的市场售价元千克关于上市时间月份的函数关系式;(2)、若图中抛物线过 , , 点,求出抛物线对应的函数关系式;(3)、由以上信息分析,几月份上市出售这种蔬菜每千克的收益最大,最大值为多少元(收益市场售价种植成本).23. 如图,在矩形 ABCD 中,E 为 BC 上一点,以 DE 为边作矩形 DEGF,其中GF 经过点 A,连接 AE.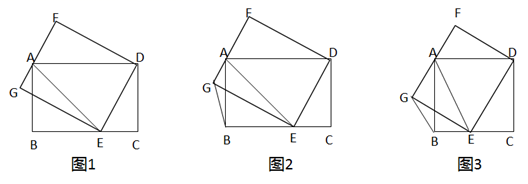 (1)、如图1,若 AE=AD,求证:AG=AF;(2)、连接BG.
(1)、如图1,若 AE=AD,求证:AG=AF;(2)、连接BG.①如图 2,若 BG=AG,CE=1,AF=2,求 AD 的长;
②如图 3,若 AB=AD,BG=BE,直接写出 的值为▲_;
24. 如图,抛物线经过点 , , 交轴于点 .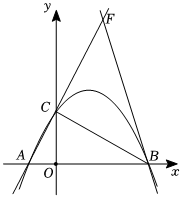 (1)、写出 , ;(2)、点为轴右侧抛物线上一点,是否存在点 , 使?若存在,求出点的坐标,若不存在,请说明理由.(3)、将直线绕点顺时针旋转 , 与直线相交于点 , 求直线的函数表达式.
(1)、写出 , ;(2)、点为轴右侧抛物线上一点,是否存在点 , 使?若存在,求出点的坐标,若不存在,请说明理由.(3)、将直线绕点顺时针旋转 , 与直线相交于点 , 求直线的函数表达式.