湖北省襄阳市谷城县2023年中考适应性考试数学试题
试卷更新日期:2023-05-18 类型:中考模拟
一、选择题(本大题共10个小题,每小题3分,共30分)
-
1. -2的倒数是( )A、 B、 C、2 D、-32. 已知直线 , 将一块含角的直角三角板( , )按如图方式放置,点A落在直线b上.若 , 的度数为( ).
 A、 B、 C、 D、3. 下列计算正确的是( ).A、 B、 C、 D、4. 下面四个立体图形中俯视图不是圆形的是( ).A、
A、 B、 C、 D、3. 下列计算正确的是( ).A、 B、 C、 D、4. 下面四个立体图形中俯视图不是圆形的是( ).A、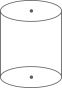 B、
B、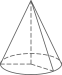 C、
C、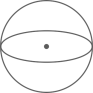 D、
D、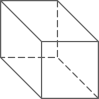 5. 中国芯是指由中国自主研发并生产制造的计算机处理芯片.目前最强的芯片制造企业是中芯,当前对外公开的,已经量产的工艺是 , 2019年就已经量产了.其中就是14纳米米 , 请将用科学记数法表示为( ).A、 B、 C、 D、6. 下列说法正确的是( ).A、篮球队员在罚球线上投篮一次,未投中是必然事件 B、任意画一个三角形,其内角和是是随机事件 C、经过有交通信号灯的路口,遇到红灯是不可能事件 D、射击运动员射击一次,命中靶心是随机事件7. 在我国古代,出现了许多著名的数学家和许多有趣的数学题目,其中有一个广为流传的题目叫“折绳测井”,原文如下:以绳测井,若将绳三折测之,绳多五尺;若将绳四折测之,绳多一尺,绳长、井深各几何?这个题目的意思是用绳子去测量井的深度,如果将绳子折成三等份后放入井中,井的外面会有5尺长的绳子;如果将绳子折成四等份后放入井中,井的外面会有1尺长的绳子.问绳子有多长?并有多深?若设井深x尺,则下列方程中正确的是( ).A、 B、 C、 D、8. 满足下列条件的四边形是正方形的是( ).A、对角线互相垂直且相等的平行四边形 B、对角线互相垂直的菱形 C、对角线相等的矩形 D、对角线互相垂直平分的四边形9. 如图,反比例函数与一次函数交于两点、 , 当时的自变量的取值范围是( ).
5. 中国芯是指由中国自主研发并生产制造的计算机处理芯片.目前最强的芯片制造企业是中芯,当前对外公开的,已经量产的工艺是 , 2019年就已经量产了.其中就是14纳米米 , 请将用科学记数法表示为( ).A、 B、 C、 D、6. 下列说法正确的是( ).A、篮球队员在罚球线上投篮一次,未投中是必然事件 B、任意画一个三角形,其内角和是是随机事件 C、经过有交通信号灯的路口,遇到红灯是不可能事件 D、射击运动员射击一次,命中靶心是随机事件7. 在我国古代,出现了许多著名的数学家和许多有趣的数学题目,其中有一个广为流传的题目叫“折绳测井”,原文如下:以绳测井,若将绳三折测之,绳多五尺;若将绳四折测之,绳多一尺,绳长、井深各几何?这个题目的意思是用绳子去测量井的深度,如果将绳子折成三等份后放入井中,井的外面会有5尺长的绳子;如果将绳子折成四等份后放入井中,井的外面会有1尺长的绳子.问绳子有多长?并有多深?若设井深x尺,则下列方程中正确的是( ).A、 B、 C、 D、8. 满足下列条件的四边形是正方形的是( ).A、对角线互相垂直且相等的平行四边形 B、对角线互相垂直的菱形 C、对角线相等的矩形 D、对角线互相垂直平分的四边形9. 如图,反比例函数与一次函数交于两点、 , 当时的自变量的取值范围是( ). A、 B、 C、或 D、或10. 二次函数的图象如图所示,下列结论:
A、 B、 C、或 D、或10. 二次函数的图象如图所示,下列结论:
①;②;③;④.其中正确的有( ).
A、1个 B、2个 C、3个 D、4个二、填空题(本大题共6个小题,每小题3分,共18分)
-
11. 代数式有意义的取值范围是.12. 不等式组的解集是.13. 有4张看上去无差别的卡片,上面分别写着1,2,3,4.随机抽取1张后,放回并混在一起,再随机抽取1张,那么第二次取出的数字能够整除第一次取出的数字的概率是.14. 飞机着陆后滑行的距离s(单位:m)关于滑行的时间t(单位:s)的函数解析式是.飞机着陆后滑行m才能停下来.15. 如图,PA、PB是的切线,切点分别为A、B,若 , 则弦AB所对的圆周角的度数为度.
 16. 如图,在正方形ABCD中,点E在边AD上,点F在边BC上,沿EF将四边形CDEF对折,点D恰好落在边AB的中点G处,求.
16. 如图,在正方形ABCD中,点E在边AD上,点F在边BC上,沿EF将四边形CDEF对折,点D恰好落在边AB的中点G处,求.
三、解答题(本大题共9个题,共72分)
-
17. 先化简,再求值: , 其中 , .18. 为庆祝中国共产主义青年团成立100周年,教育主管部门在A、B两市各抽取50名团员开展团知识竞赛,为便于统计成绩,制定了取整数的计分方式,满分100分.整理分析过程如下:
【收集数据】A市50名团员中,知识竞赛在组的具体数据如下:
82,82,82,82,82,84,84,85,86,86,86,86,87,88.
【整理数据】不完整的两所学校的频数分布表如下
组别
A市
2
6
a
14
13
B市
1
9
15
13
12
不完整的A市成绩频数分布直方图如图所示:
A市知识竞赛频数分布直方图

【分析数据】两组数据的平均数、众数、中位数、方差如下表:
特征数
平均数
众数
中位数
方差
A市
80.9
82
b
118.79
B市
80.8
95
80
109.95
根据以上信息,回答下列问题:
(1)、本次调查是调查(选填“抽样”或“全面”);(2)、统计表中, , ;(3)、补全频数分布直方图;(4)、在这次调查中,竞赛成绩波动较小的是市(选填“A”或“B”);(5)、按此次结果估算,了解共青团知识得分不低于80分,估计两个城市8000名团员中,能得到了解共青团知识(不低于80分)的团员共有人.19. 小军与小明放学后看见楼前的小广场上有一架无人机正在定点拍摄小区全景,此时如图所示,小军在一楼B处测得无人机C的仰角 , 在楼顶A处的小明测得无人机C的仰角 , 他们所在的楼高约为120米,求此时无人机C离地面BE的高度.(参考数据: , , , ) 20. 如图,BE是中的角平分线,交AD于点E.
20. 如图,BE是中的角平分线,交AD于点E. (1)、作的角平分线,交BC于点F.(尺规作图,不写作法,保留作图痕迹);(2)、证明:.21. 已知关于x的一元二次方程有两个不相等的实数根 , .(1)、求k的取值范围;(2)、若 , 求k的值.22. 如图,是等腰直角三角形, , 以BC为直径作交斜边AB于点D,点M是中点,过点M作直线于点E,交AC于点F.
(1)、作的角平分线,交BC于点F.(尺规作图,不写作法,保留作图痕迹);(2)、证明:.21. 已知关于x的一元二次方程有两个不相等的实数根 , .(1)、求k的取值范围;(2)、若 , 求k的值.22. 如图,是等腰直角三角形, , 以BC为直径作交斜边AB于点D,点M是中点,过点M作直线于点E,交AC于点F. (1)、证明:EF是的切线;(2)、若 , 求图中阴影部分面积.23. 市政府为了加大各部门和单位对口扶贫力度,某单位对帮扶对象种植的两种农产品A、B联系超市助销.该超市购买A产品进价为;B产品的进货量超过的部分有优惠,且B产品的付款金额y(单位:元)与进货量x(单位:)之间都是一次函数关系,下表所示部分付款情况,该超市对A产品的售价定为 , B产品的售价定为.
(1)、证明:EF是的切线;(2)、若 , 求图中阴影部分面积.23. 市政府为了加大各部门和单位对口扶贫力度,某单位对帮扶对象种植的两种农产品A、B联系超市助销.该超市购买A产品进价为;B产品的进货量超过的部分有优惠,且B产品的付款金额y(单位:元)与进货量x(单位:)之间都是一次函数关系,下表所示部分付款情况,该超市对A产品的售价定为 , B产品的售价定为.B产品进货量
0
100
300
500
700
900
1000
付款金额y元
0
I500
4500
7500
9900
12300
13500
(1)、求出和时,y与x之间的函数关系式;(2)、若该超市购进A、B两种产品共 , 并全部售出.但超市要求B产品的进货量不低于 , 且不高于 , 设销售完A、B两种产品所获总利润为w元(利润销售额成本),请求出w(单位:元)与B种产品进货量x(单位:)之间的函数关系式,并为该超市设计出获得最大利润的进货方案;(3)、为了加快扶贫进度,超市决定对两种产品让利销售.在(2)中获得最大利润的进货方案下,售出A或B产品每千克都提出元的帮扶资金返给农户,全部售出后所获总利润不低于5500元,求a的最大值.24. 在和中, , , 点D在线段AC上.


图(1) 图(2) 图(3)
(1)、【特例证明】如图(1),当时, , 证明:;
(2)、【类比探究】如图(2),当 , 点D是线段AC上任一点时,证明:①;②;
(3)、【拓展运用】如图(3),当时, , , 求BC长.
25. 已知直线与x轴交于点A,与y轴交于点B,抛物线恰好经过A、B两点且与x轴交于另一点C(在点A左侧).

图(1) 图(2)
(1)、求抛物线解析式;(2)、如图(1),点D是抛物线上在第一象限上的一点,点E是平面内一点,四边形ADBE是平行四边形,当的面积为时,求出点D的坐标;(3)、如图(2),点D是抛物线上在第一象限上的一点,点F是平面内一点,四边形DBCF是平行四边形,连接CD交AB于点M,AB交DF于点N,设的面积表示为 , 的面积表示为 , 的面积表示为 , 求的最大值.