湖北省武汉市新观察2023年中考数学模拟试卷(三)
试卷更新日期:2023-05-18 类型:中考模拟
一、选择题(本大题共10小题,共30.0分。)
-
1. 实数-2023的相反数是( )A、-2023 B、 C、2023 D、2. 买一张电影票,座位号是偶数号这个事件是( )A、必然事件 B、不可能事件 C、随机事件 D、确定性事件3. 下列图形中既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 计算(2a4)3的结果是( )A、 B、 C、 D、5. 如图所示的几何体是由6个大小相同的小正方体组成,它的主视图是( )
4. 计算(2a4)3的结果是( )A、 B、 C、 D、5. 如图所示的几何体是由6个大小相同的小正方体组成,它的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. , 是反比例函数的图象上的两点,若 , 则下列结论正确的是( )A、 B、 C、 D、7. 将一圆柱形小水杯固定在大圆柱形容器底面中央,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯水面的高度与注水时间的函数图象大致是( )
6. , 是反比例函数的图象上的两点,若 , 则下列结论正确的是( )A、 B、 C、 D、7. 将一圆柱形小水杯固定在大圆柱形容器底面中央,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯水面的高度与注水时间的函数图象大致是( ) A、
A、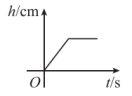 B、
B、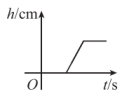 C、
C、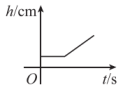 D、
D、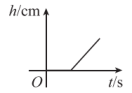 8. 如图所示,电路连接完好,且各元件工作正常随机闭合开关 , , 中的两个,能让两个小灯泡同时发光的概率是( )
8. 如图所示,电路连接完好,且各元件工作正常随机闭合开关 , , 中的两个,能让两个小灯泡同时发光的概率是( ) A、 B、 C、 D、9. 根据一周7天可以制作出每年的“星期几密码”现已知2035年的“星期几密码”是“033614625035”,这组密码中从左到右的12个数字依次与2035年的1到12月对应,我们可以用这组密码算出年某天是星期几.如年月日,其中月对应密码中的第二个数字“3”,将数字3加上日期8,其和为11,再把11除以7,得余数4,则该天为星期四余数几则对应星期几,特别地,余数0则对应星期天利用此密码算出2035年的世界环境日(6月5日是( )A、星期一 B、星期二 C、星期四 D、星期六10. 如图,、为的两条弦, , , 将劣弧折叠后刚好过弦的中点 , 则的半径为( )
A、 B、 C、 D、9. 根据一周7天可以制作出每年的“星期几密码”现已知2035年的“星期几密码”是“033614625035”,这组密码中从左到右的12个数字依次与2035年的1到12月对应,我们可以用这组密码算出年某天是星期几.如年月日,其中月对应密码中的第二个数字“3”,将数字3加上日期8,其和为11,再把11除以7,得余数4,则该天为星期四余数几则对应星期几,特别地,余数0则对应星期天利用此密码算出2035年的世界环境日(6月5日是( )A、星期一 B、星期二 C、星期四 D、星期六10. 如图,、为的两条弦, , , 将劣弧折叠后刚好过弦的中点 , 则的半径为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
11. 据国家统计局统计,我国2022年国民生产总值为1210000亿元用科学记数法表示1210000亿元是 元12. 2022年北京冬奥会激起某校学生学习冬奥知识的热情为了引领学生更深入地学习,学校组织了一次知识竞赛,随机抽取6名同学的分数单位:分如下:80,90,85, , 86,88,则这6个数据的中位数是 .13. 计算的结果是 .14. 如图,从热气球上测得两建筑物、底部的俯角分别为和 , 如果这时气球的高度为100米,且点、、在同一直线上,则建筑物、之间的距离约为 米结果精确到1米, , , .
 15. 下列关于抛物线为常数的结论:
15. 下列关于抛物线为常数的结论:抛物线的对称轴为直线;抛物线的顶点在直线上;抛物线与轴的交点在原点的上方;抛物线上有两点 , , 若 , , 则其中正确结论的序号是 .
16. 如图,等腰直角 , , 点为外一点, , 将绕点顺时针旋转至 , 交于点,若 , , 则的长为 .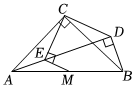
三、解答题(本大题共8小题,共72.0分。)
-
17. 解不等式组请按下列步骤完成解答.(1)、解不等式 , 得 ;(2)、解不等式 , 得 ;(3)、把不等式和的解集在数轴上表示出来;
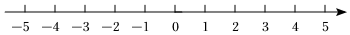 (4)、原不等式组的解集是 .18. 如图,已知 , , , , 射线 .
(4)、原不等式组的解集是 .18. 如图,已知 , , , , 射线 . (1)、判断射线与的位置关系,并说明理由;(2)、求 , 的度数.19. 某校学生会向全校3000名学生发起了“爱心捐助”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如图所示的统计图.
(1)、判断射线与的位置关系,并说明理由;(2)、求 , 的度数.19. 某校学生会向全校3000名学生发起了“爱心捐助”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如图所示的统计图.
请根据相关信息,解答下列问题:
(1)、本次接受随机调查的学生人数为 ,图1中的值是 ;(2)、求本次调查获取的样本数据的平均数;(3)、根据样本数据,估计该校本次活动捐款金额为10元的学生人数.20. 如图,在中,是上一点, , 平分交于点 , 连结 , .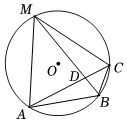 (1)、求证:是正三角形;(2)、若 , 求半径的长.21. 如图是由边长为的小正方形构成的网格.每个小正方形的顶点叫做格点.的顶点在格点上,仅用无刻度尺的直尺在给定网格中画图.画图过程用虚线表示.画图结果用实线表示,完成下列问题:
(1)、求证:是正三角形;(2)、若 , 求半径的长.21. 如图是由边长为的小正方形构成的网格.每个小正方形的顶点叫做格点.的顶点在格点上,仅用无刻度尺的直尺在给定网格中画图.画图过程用虚线表示.画图结果用实线表示,完成下列问题:
⑴ ▲ ;
⑶将边绕点顺时针旋转得到线段则 ▲ ;
⑶画出的外接圆的圆心;
⑷在上确定一点 , 使 .
22. 某花店在一段时间内推销一种新型花卉,经过统计发现:销售量株与销售时间第为正整数天的变化情况,获得部分数据如表:1
2
3
4
5
31
56
75
88
95
(1)、请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定与之间的函数关系式;(2)、花店第几天获得的销售量最大?最多销售多少株?(3)、花店为了扩大影响,计划连续6天的销售利润不得低于为正整数株,请直接写出的最小值.23. 如图 (1)、【问题提出】
(1)、【问题提出】
如图1,在中, , , 是等边三角形,点在边上,探究与的数量关系.(2)、【问题探究】
先将问题特殊化如图1,当点在边上时,猜想和数量关系,并加以证明;(3)、再探究一般情形如图2,当点在内部时,证明(1)中的结论仍然成立.(4)、【问题拓展】
如图3,当点在外部时,于点 , 过点作 , 交线段的延长线于点 , , 直接写出的长 .24. 已知抛物线与轴交于点和点 , 与轴负半轴交于点 , 且 , 抛物线的顶点为 .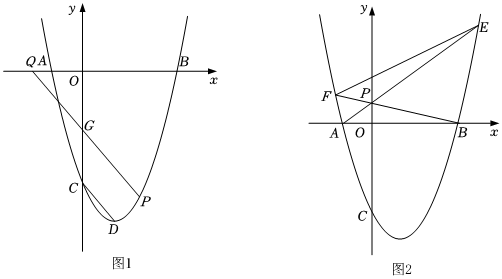 (1)、求抛物线的解析式;(2)、如图1,为抛物线的顶点,分别与轴,轴交于 , 两点,若 , 求点坐标;(3)、如图2,点在轴正半轴上,、延长线交抛物线于、两点,若 , 求点的坐标.
(1)、求抛物线的解析式;(2)、如图1,为抛物线的顶点,分别与轴,轴交于 , 两点,若 , 求点坐标;(3)、如图2,点在轴正半轴上,、延长线交抛物线于、两点,若 , 求点的坐标.