湖北省武汉市洪山区东片区2023年中考数学联考试卷(3月)
试卷更新日期:2023-05-18 类型:中考模拟
一、选择题(本大题共10小题,共30.0分。)
-
1. 实数-2的相反数是( )A、-2 B、2 C、 D、2. 下列事件中是必然事件的是( )A、打开电视机,正在播放电视剧觉醒年代 B、抛掷一枚质地均匀的骰子,点数六朝上 C、随意翻到新华字典的某页,这一页的页码是奇数 D、通常温度降到以下,纯净的水结冰3. 在美术字中,有些汉字或字母是中心对称图形下面的汉字或字母不是中心对称图形的是( )A、
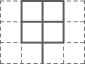 B、
B、 C、
C、 D、
D、 4. 计算的结果是( )A、 B、 C、 D、5. 如图是由4个相同的小正方体组成的几何体,它的左视图是( )
4. 计算的结果是( )A、 B、 C、 D、5. 如图是由4个相同的小正方体组成的几何体,它的左视图是( )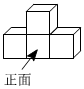 A、
A、 B、
B、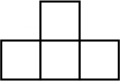 C、
C、 D、
D、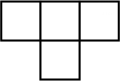 6. 在单词数学中任意选择一个字母,字母为元音字母、、、、的概率是( )A、 B、 C、 D、7. 我国古代数学名著《九章算术》中记载:“今有竹高一丈、末折抵地,去本三尺问折者高几何?翻译:现有竹子高一丈,折断的末端撑着地,离地面竹根三尺远,问折断处离地面有多高?(1丈=10尺)设折断处离地的高度为尺,则下列方程正确的是( )A、 B、 C、 D、8. 甲,乙两车从地驶向地,并以各自的速度匀速行驶,甲车比乙车早行驶 , 并且甲车途中休息了 , 如图是甲,乙两车行驶的路程与甲车行驶的时间的函数图象,则在乙车行驶的过程中两车相距时,乙车行驶的时间为( )
6. 在单词数学中任意选择一个字母,字母为元音字母、、、、的概率是( )A、 B、 C、 D、7. 我国古代数学名著《九章算术》中记载:“今有竹高一丈、末折抵地,去本三尺问折者高几何?翻译:现有竹子高一丈,折断的末端撑着地,离地面竹根三尺远,问折断处离地面有多高?(1丈=10尺)设折断处离地的高度为尺,则下列方程正确的是( )A、 B、 C、 D、8. 甲,乙两车从地驶向地,并以各自的速度匀速行驶,甲车比乙车早行驶 , 并且甲车途中休息了 , 如图是甲,乙两车行驶的路程与甲车行驶的时间的函数图象,则在乙车行驶的过程中两车相距时,乙车行驶的时间为( )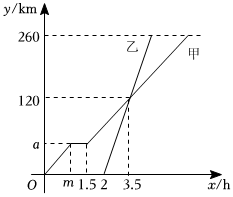 A、或 B、或 C、或 D、或9. 有一张矩形纸片 , 已知 , , 上面有一个以为直径的半圆,如图甲,将它沿折叠,使点落在上,如图乙,这时,半圆还露在外面的部分阴影部分的面积是( )
A、或 B、或 C、或 D、或9. 有一张矩形纸片 , 已知 , , 上面有一个以为直径的半圆,如图甲,将它沿折叠,使点落在上,如图乙,这时,半圆还露在外面的部分阴影部分的面积是( ) A、 B、 C、 D、10. 已知 , 是方程的两根,则代数式的值是( )A、18 B、-18 C、27 D、-27
A、 B、 C、 D、10. 已知 , 是方程的两根,则代数式的值是( )A、18 B、-18 C、27 D、-27二、填空题(本大题共6小题,共18.0分)
-
11. 化简的结果是 .12. 一家公司某部门名员工的月薪单位:元分别是:8000,2550,4599,1700,980,2480,1976,这组数据的中位数是 .13. 已知点 , 在反比例函数是常数的图象上,且 , 则的取值范围是 .14. 如图,小林同学为了测量某世界名楼的高度,他站在处仰望楼顶 , 仰角为 , 走到点处仰望楼顶 , 仰角为 , 眼睛、离同一水平地面的高度为米,米,则楼顶离地面的高度约是 米取 , 取 , 按四舍五入法将结果精确到 .
 15. 已知抛物线是常数 , , 且图象经过下列四个结论:;;当时,对于任意实数 , 有;当时,方程有两个不相等的实数根其中正确的是 填写序号 .16. 如图,是等边三角形,是的中点,是边上一动点,且从以个单位每秒的速度向出发设 , , 关于的函数图象过点 , 则图象最低点的坐标是 .
15. 已知抛物线是常数 , , 且图象经过下列四个结论:;;当时,对于任意实数 , 有;当时,方程有两个不相等的实数根其中正确的是 填写序号 .16. 如图,是等边三角形,是的中点,是边上一动点,且从以个单位每秒的速度向出发设 , , 关于的函数图象过点 , 则图象最低点的坐标是 .
三、解答题(本大题共8小题,共72.0分。)
-
17. 解不等式组请按下列步骤完成解答:
 (1)、解不等式 , 得 ;(2)、解不等式 , 得 ;(3)、把不等式和的解集在数轴上表示出来;(4)、原不等式组的解集为 .18. 如图,点、、分别是三角形的边、、上的点, , .
(1)、解不等式 , 得 ;(2)、解不等式 , 得 ;(3)、把不等式和的解集在数轴上表示出来;(4)、原不等式组的解集为 .18. 如图,点、、分别是三角形的边、、上的点, , . (1)、求证: .(2)、若:: , , 求 .19. 推行“双减”政策后,为了解某市初中生每周校外锻炼身体的时长单位:小时的情况,在全市随机抽取部分初中生进行调查,按五个组别:组 , 组 , 组 , 组 , 组进行整理,绘制如下两幅不完整的统计图,根据图中提供的信息,解决下列问题:
(1)、求证: .(2)、若:: , , 求 .19. 推行“双减”政策后,为了解某市初中生每周校外锻炼身体的时长单位:小时的情况,在全市随机抽取部分初中生进行调查,按五个组别:组 , 组 , 组 , 组 , 组进行整理,绘制如下两幅不完整的统计图,根据图中提供的信息,解决下列问题: (1)、这次抽样调查的样本容量是 , 组所在扇形的圆心角的大小是;(2)、将频数分布直方图补充完整;(3)、若该市共有5万名初中生,请你估计该市每周校外锻炼身体时长不少于6小时的初中学生人数.20. 如图,为的切线,为切点,过作的垂线 , 垂足为点交于点 , 延长与交于点 , 与的延长线交于点 .
(1)、这次抽样调查的样本容量是 , 组所在扇形的圆心角的大小是;(2)、将频数分布直方图补充完整;(3)、若该市共有5万名初中生,请你估计该市每周校外锻炼身体时长不少于6小时的初中学生人数.20. 如图,为的切线,为切点,过作的垂线 , 垂足为点交于点 , 延长与交于点 , 与的延长线交于点 .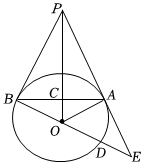 (1)、求证:为的切线;(2)、若 , 求 .21. 如图是由边长为1的小正方形组成的网格,的顶点均在格点上仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示,画图结果用实线表示.
(1)、求证:为的切线;(2)、若 , 求 .21. 如图是由边长为1的小正方形组成的网格,的顶点均在格点上仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示,画图结果用实线表示.
⑴在图(1)中画的高;
⑵在图(1)的线段上画一点 , 使得::;
⑶在图(2)中点的右侧画一点 , 使且 .
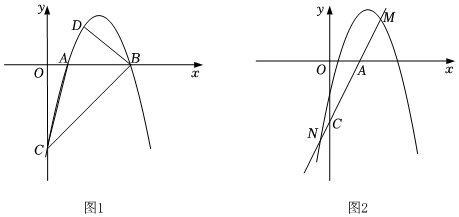
22. 北京冬奥会的召开激起了人们对冰雪运动的极大热情,如图是某小型跳台滑雪训练场的横截面示意图,取某一位置的水平线为轴,过跳台终点作水平线的垂线为轴,建立平面直角坐标系,图中的抛物线:近似表示滑雪场地上的一座小山坡,某滑雪爱好者小张从点正上方点滑出,滑出后沿一段抛物线:运动. (1)、当小张滑到离处的水平距离为米时,其滑行高度最大,为米,直接写出 , 的值;(2)、在(1)的条件下,当小张滑出后离的水平距离为多少米时,他滑行高度与小山坡的竖直距离为米?(3)、小张从点滑出,滑行的高度恰好在坡顶正上方时,与坡顶距离不低于3米,求此时 , 的值或取值范围.
(1)、当小张滑到离处的水平距离为米时,其滑行高度最大,为米,直接写出 , 的值;(2)、在(1)的条件下,当小张滑出后离的水平距离为多少米时,他滑行高度与小山坡的竖直距离为米?(3)、小张从点滑出,滑行的高度恰好在坡顶正上方时,与坡顶距离不低于3米,求此时 , 的值或取值范围.