湖北省武汉市2023年中考一模数学试卷
试卷更新日期:2023-05-18 类型:中考模拟
一、选择题(共10小题,每小题3分,共30分)
-
1. 实数3的相反数是( )A、3 B、 C、 D、-32. “一箭双雕”这个事件是( )A、不可能事件 B、必然事件 C、随机事件 D、确定性事件3. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )A、吉 B、祥 C、如 D、意4. 计算的结果是( )A、 B、 C、 D、5. 如图是由4个相同的小正方体组成的几何体,它的左视图是( )
 A、
A、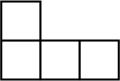 B、
B、 C、
C、 D、
D、 6. 1个不透明布袋中装有除颜色外没有其他区别的1个红球和3个白球,从中摸出1个球不放回,再摸出1个球,两次都摸出白球的概率是( )A、 B、 C、 D、7. 如图,将挂在弹簧测力计下端的铁块浸没于水中,然后缓慢匀速向上提起,直至铁块完全露出水面一定高度,下图能大致反映弹簧测力计的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的图象是( )
6. 1个不透明布袋中装有除颜色外没有其他区别的1个红球和3个白球,从中摸出1个球不放回,再摸出1个球,两次都摸出白球的概率是( )A、 B、 C、 D、7. 如图,将挂在弹簧测力计下端的铁块浸没于水中,然后缓慢匀速向上提起,直至铁块完全露出水面一定高度,下图能大致反映弹簧测力计的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的图象是( )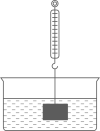 A、
A、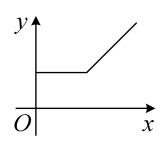 B、
B、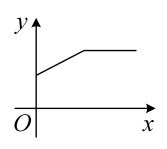 C、
C、 D、
D、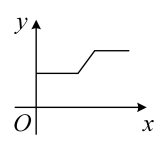 8. 若点 , 在反比例函数的图象上,且 , 则a的取值范围是( )A、 B、 C、 D、或9. 如图,在平行四边形ABCD中,AB为的直径,与DC相切于点E,与AD相交于点F,已知 , , 则图中阴影部分面积是( )
8. 若点 , 在反比例函数的图象上,且 , 则a的取值范围是( )A、 B、 C、 D、或9. 如图,在平行四边形ABCD中,AB为的直径,与DC相切于点E,与AD相交于点F,已知 , , 则图中阴影部分面积是( ) A、 B、 C、 D、10. 如果m,n是两个不相等的实数,且满足 , , 那么代数式的值是( )A、16 B、15 C、12 D、9
A、 B、 C、 D、10. 如果m,n是两个不相等的实数,且满足 , , 那么代数式的值是( )A、16 B、15 C、12 D、9二、填空题(共6小题,每小题3分,共18分)
-
11. 计算 的结果是12. 某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成如下统计表,这组数据的中位数是 .
一分钟跳绳个数
141
142
144
145
146
学生人数
3
2
2
1
2
13. 计算的结果是 .14. 一艘在南北航线上的测量船,在点A处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达点C时,测得海岛B在点C的北偏东45°方向,那么海岛B离此航线的最近距离是(结果保留整数).(参考数据: , )15. 二次函数(a,b,c为常数)中的x与y的部分对应值如下表:x
-1.4
0
1
2.4
y
-1.4
2.4
5
2.4
①;
②当时,y的值随x值的增大而减小;
③-1.4是方程的一个根;
④当时, .
以上结论正确的是(填序号).
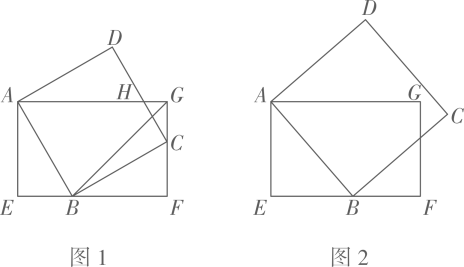
16. 如图,菱形ABCD的边 , , E是AB的中点,F是边CD上一点,将四边形AEFD沿直线EF折叠,A的对应点为 , 当的长度最小时,CF的长是 .
三、解答题(共8小题,共72分)
-
17. 解不等式组请按下列步骤完成解答.(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来;
 (4)、原不等式组的解集是 .18. 如图,BE是△ABC的角平分线,点D在AB上,且 .
(4)、原不等式组的解集是 .18. 如图,BE是△ABC的角平分线,点D在AB上,且 .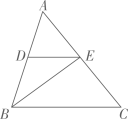 (1)、求证:;(2)、若 , , 求的大小.19. 某校为了解学生课外阅读时间情况,随机抽取了a名学生,根据平均每天课外阅读时间的长短,将他们分为A,B,C,D四个小组,并制作了如下不完整的频数分布表和扇形统计图.
(1)、求证:;(2)、若 , , 求的大小.19. 某校为了解学生课外阅读时间情况,随机抽取了a名学生,根据平均每天课外阅读时间的长短,将他们分为A,B,C,D四个小组,并制作了如下不完整的频数分布表和扇形统计图.平均每天课外阅读时间频数分布表
小组
时间(小时)
频数
A
10
B
20
C
b
D
c

请根据图表中的信息解答下列问题.
(1)、直接写出a,b,c的值;(2)、该校现有1200名学生,请估计该校有多少名学生平均每天课外阅读时间不少于1小时.20. 如图,E是的内心,AE的延长线与的外接圆相交于点D.
求证:
(1)、;(2)、若 , , 求DE的长.21. 如图是由小正方形组成的12×11网格,每个小正方形的顶点叫作格点,过格点A,B,C的圆交于点F,点G在DE上,其中D,G是格点.仅用无刻度的直尺在给定网格中按要求完成画图,画图过程用虚线表示.
⑴在AD的下方画出正方形ADMN;
⑵画出圆心O;
⑶画出的中点P;
⑷画出线段AE绕点A逆时针旋转90°后的对应线段AQ.
22. 某商场经营某种商品,该商品的进价为30元/件,根据市场调查发现,该商品每周的销售量y(单位:件)与售价x(单位:元/件)(x为正整数)之间满足一次函数的关系,下表记录的是某三周的有关数据.x(元/件)
50
60
70
y(件)
1000
900
800
(1)、求y关于x的函数关系式(不求自变量的取值范围);(2)、若某周该商品的销售量不少于700件,求这周该商场销售这种商品获得的最大利润;(3)、规定这种商品的售价不超过进价的2倍,若商品的进价每件提高m元()时,该商场每周销售这种商品的利润仍随售价的增大而增大,请直接写出m的取值范围.