湖北省天门市、仙桃市、潜江市2023年中考数学一模试卷
试卷更新日期:2023-05-18 类型:中考模拟
一、选择题(本大题共10小题,共30.0分。)
-
1. 下列实数中,比-5小的数是( )A、-6 B、 C、0 D、2. 如图是《九章算术》中“堑堵”的立体图形,它的左视图为( )
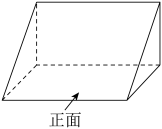 A、
A、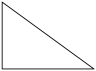 B、
B、 C、
C、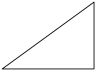 D、
D、 3. 下列各式运算正确的是( )A、 B、 C、 D、4. 下列说法正确的是( )A、了解一批灯泡的使用寿命,应采用抽样调查的方式 B、如果某彩票的中奖概率是1%,那么一次购买100张这种彩票一定会中奖 C、若甲、乙两组数据的平均数相同, , , 则乙组数据较稳定 D、“任意掷一枚质地均匀的骰子,掷出的点数是7”是必然事件5. 如图,直线 , 于点 , , 则的度数为( )
3. 下列各式运算正确的是( )A、 B、 C、 D、4. 下列说法正确的是( )A、了解一批灯泡的使用寿命,应采用抽样调查的方式 B、如果某彩票的中奖概率是1%,那么一次购买100张这种彩票一定会中奖 C、若甲、乙两组数据的平均数相同, , , 则乙组数据较稳定 D、“任意掷一枚质地均匀的骰子,掷出的点数是7”是必然事件5. 如图,直线 , 于点 , , 则的度数为( ) A、 B、 C、 D、6. 已知圆锥的底面半径为5,高为12,则它的侧面展开图的面积是( )A、 B、 C、 D、7. 一次函数和反比例函数在同一个平面直角坐标系中的图象如图所示,则二次函数的图象可能是( )
A、 B、 C、 D、6. 已知圆锥的底面半径为5,高为12,则它的侧面展开图的面积是( )A、 B、 C、 D、7. 一次函数和反比例函数在同一个平面直角坐标系中的图象如图所示,则二次函数的图象可能是( ) A、
A、 B、
B、 C、
C、 D、
D、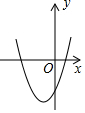 8. 已知关于的方程的两实数根为 , , 若 , 则的值为( )A、-3 B、-1 C、-3或1 D、-1或39. 如图,在网格正方形中,每个小正方形的边长为1,顶点为格点,若的顶点均是格点,则的值是( )
8. 已知关于的方程的两实数根为 , , 若 , 则的值为( )A、-3 B、-1 C、-3或1 D、-1或39. 如图,在网格正方形中,每个小正方形的边长为1,顶点为格点,若的顶点均是格点,则的值是( ) A、 B、 C、 D、10. 如图,四边形是边长为的正方形,点E,点F分别为边 , 中点,点O为正方形的中心,连接 , 点P从点E出发沿运动,同时点Q从点B出发沿运动,两点运动速度均为 , 当点P运动到点F时,两点同时停止运动,设运动时间为 , 连接 , 的面积为 , 下列图像能正确反映出S与t的函数关系的是( )
A、 B、 C、 D、10. 如图,四边形是边长为的正方形,点E,点F分别为边 , 中点,点O为正方形的中心,连接 , 点P从点E出发沿运动,同时点Q从点B出发沿运动,两点运动速度均为 , 当点P运动到点F时,两点同时停止运动,设运动时间为 , 连接 , 的面积为 , 下列图像能正确反映出S与t的函数关系的是( )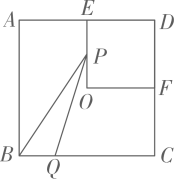 A、
A、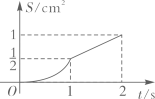 B、
B、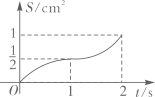 C、
C、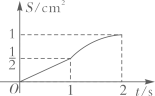 D、
D、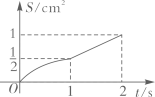
二、填空题(本大题共5小题,共15.0分)
-
11. 石墨烯是目前世界上最薄却最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.00000000034米,将这个数用科学记数法表示为 .12. 有A,B两种医用外科口罩,2包A型口罩与3包B型口罩合计27元,7包A型口罩与8包B型口罩合计77元,则3包A型口罩与2包B型口罩合计元.13. 假期前,小明家设计了三种度假方案:参观动植物园、看电影、近郊露营.妈妈将三种方案分别写在三张相同的卡片上,小明随机抽取1张后,放回并混在一起,姐姐再随机抽取1张,则小明和姐姐抽取的度假方案相同的概率是 .14. 已知点在一个反比例函数的图象上,点与点关于轴对称.若点在正比例函数的图象上,则这个反比例函数的表达式为 .15. 如图,是的直径,点是上一点,与过点的切线垂直,垂足为点 , 直线与的延长线相交于点 , 弦平分 , 交于点 , 连接 , 下列四个结论中:平分;;;若 , , 则的长为其中正确的结论有:写出所有正确结论的序号

三、计算题(本大题共1小题,共10.0分)
-
16. 某果园有果树60棵,现准备多种一些果树提高果园产量.如果多种树,那么树之间的距离和每棵果树所受光照就会减少,每棵果树的平均产量随之降低.根据经验,增种10棵果树时,果园内的每棵果树平均产量为在确保每棵果树平均产量不低于的前提下,设增种果树且为整数棵,该果园每棵果树平均产量为 , 它们之间的函数关系满足如图所示的图象.
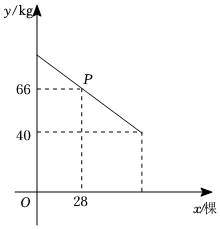 (1)、图中点所表示的实际意义是 , 每增种1棵果树时,每棵果树平均产量减少;(2)、求与之间的函数关系式,并直接写出自变量的取值范围;(3)、当增种果树多少棵时,果园的总产量最大?最大产量是多少?
(1)、图中点所表示的实际意义是 , 每增种1棵果树时,每棵果树平均产量减少;(2)、求与之间的函数关系式,并直接写出自变量的取值范围;(3)、当增种果树多少棵时,果园的总产量最大?最大产量是多少?四、解答题(本大题共8小题,共65.0分。)
-
17.(1)、计算:;(2)、解方程: .18. 某校在九年级学生中随机抽取了若干名学生参加“平均每天体育运动时间”的调查,根据调查结果绘制了如下不完整的频数分布表和频数分布直方图.
频数分布表
运动时间t/min
频数
频率
4
0.1
7
0.175
a
0.35
9
0.225
6
b
合计
n
1
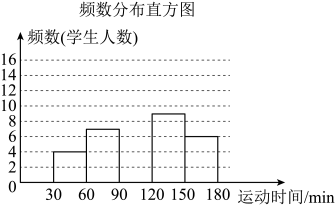
请根据图表中的信息解答下列问题:
(1)、频数分布表中的a= , b= , n=;(2)、请补全频数分布直方图;(3)、若该校九年级共有480名学生,试估计该校九年级学生平均每天体育运动时间不低于120 min的学生人数.19. 如图,在▱中,点在上, , 平分交于点 , 请用无刻度的直尺画图保留作图痕迹,不写画法 .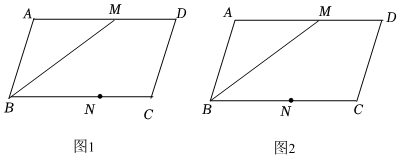 (1)、在图1中,过点画出中边上的高 , 并证明你的结论;(2)、在图2中,过点画出到的垂线段 .20. 某班同学在一次综合实践课上,测量校园内一棵树的高度.如图,测量仪在处测得树顶的仰角为 , 处测得树顶的仰角为点 , , 在一条水平直线上 , 已知测量仪高度米,米,求树的高度结果保留小数点后一位.参考数据: , , .
(1)、在图1中,过点画出中边上的高 , 并证明你的结论;(2)、在图2中,过点画出到的垂线段 .20. 某班同学在一次综合实践课上,测量校园内一棵树的高度.如图,测量仪在处测得树顶的仰角为 , 处测得树顶的仰角为点 , , 在一条水平直线上 , 已知测量仪高度米,米,求树的高度结果保留小数点后一位.参考数据: , , . 21. 如图,正比例函数y= x的图象与反比例函数y= (k≠0)的图象都经过点A(a,2).
21. 如图,正比例函数y= x的图象与反比例函数y= (k≠0)的图象都经过点A(a,2).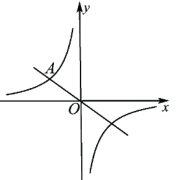 (1)、求点A的坐标和反比例函数表达式.(2)、若点P(m,n)在该反比例函数图象上,且它到y轴距离小于3,请根据图象直接写出n的取值范围.22. 如图,以为直径的经过的顶点 , , 分别平分和 , 的延长线交于点 , 连接.
(1)、求点A的坐标和反比例函数表达式.(2)、若点P(m,n)在该反比例函数图象上,且它到y轴距离小于3,请根据图象直接写出n的取值范围.22. 如图,以为直径的经过的顶点 , , 分别平分和 , 的延长线交于点 , 连接.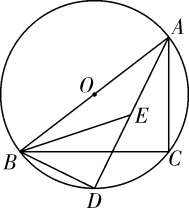 (1)、判断的形状,并证明你的结论;(2)、若 , , 求的长.23. 【推理】
(1)、判断的形状,并证明你的结论;(2)、若 , , 求的长.23. 【推理】如图1,在正方形中,点是上一动点,将正方形沿着折叠,点落在点处,连结 , , 延长交于点 .
 (1)、求证:≌ .(2)、如图2,在【推理】条件下,延长交于点若 , , 求线段的长.(3)、将正方形改成矩形,同样沿着折叠,连结 , 延长 , 交直线于 , 两点,若 , , 求的值用含的代数式表示 .24. 在平面直角坐标系中,抛物线与轴交于点 , 其对称轴与轴交于点 .(1)、求点 , 的坐标;(2)、若 , 当时,二次函数的最大值为-1,求的值;(3)、直线经过点 , 将点向右平移6个单位长度,得到点 , 若抛物线与线段只有一个公共点,结合函数图象,请直接写出的取值范围.
(1)、求证:≌ .(2)、如图2,在【推理】条件下,延长交于点若 , , 求线段的长.(3)、将正方形改成矩形,同样沿着折叠,连结 , 延长 , 交直线于 , 两点,若 , , 求的值用含的代数式表示 .24. 在平面直角坐标系中,抛物线与轴交于点 , 其对称轴与轴交于点 .(1)、求点 , 的坐标;(2)、若 , 当时,二次函数的最大值为-1,求的值;(3)、直线经过点 , 将点向右平移6个单位长度,得到点 , 若抛物线与线段只有一个公共点,结合函数图象,请直接写出的取值范围.
-