四川省德阳市什邡市2023年中考一模数学试题
试卷更新日期:2023-05-18 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 下列各式中,计算正确的是( )A、 B、 C、 D、3. 2022年中国与“一带一路”沿线国家货物贸易进出口总额达到13800亿美元,用科学记数法表示13800是( )A、 B、 C、 D、4. 实数a、b、c满足a>b且ac<bc,它们在数轴上的对应点的位置可以是( )A、
 B、
B、 C、
C、 D、
D、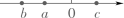 5. 如图所示的几何体的左视图是( )
5. 如图所示的几何体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 在光明中学组织的全校师生迎“五四”诗词大赛中,来自不同年级的25名参赛同学的得分情况如图所示.这些成绩的中位数和众数分别是( )
6. 在光明中学组织的全校师生迎“五四”诗词大赛中,来自不同年级的25名参赛同学的得分情况如图所示.这些成绩的中位数和众数分别是( )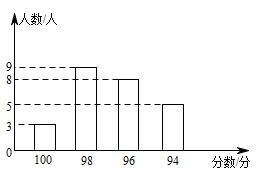 A、96分,98分 B、97分,98分 C、98分,96分 D、97分,96分7. 若不等式组 无解,则 的取值范围为( )A、 B、 C、 D、8. 如图, 是半圆 的直径, , 是 上两点,连接 , 并延长交于点 ,连接 , ,如果 ,那么 的度数为( )
A、96分,98分 B、97分,98分 C、98分,96分 D、97分,96分7. 若不等式组 无解,则 的取值范围为( )A、 B、 C、 D、8. 如图, 是半圆 的直径, , 是 上两点,连接 , 并延长交于点 ,连接 , ,如果 ,那么 的度数为( )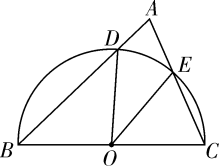 A、 B、 C、 D、9. 若关于x的一元二次方程有实数根,则k的取值范围为( )A、 B、且 C、 D、且10. 某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲,乙两仓库的快件数量 (件)与时间 (分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )
A、 B、 C、 D、9. 若关于x的一元二次方程有实数根,则k的取值范围为( )A、 B、且 C、 D、且10. 某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲,乙两仓库的快件数量 (件)与时间 (分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )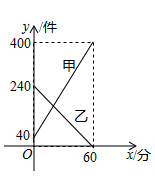 A、9:15 B、9:20 C、9:25 D、9:3011. 如图,在 中, , ,点 在边 上,且 ,点 为 的中点,点 为边 上的动点,当点 在 上移动时,使四边形 周长最小的点 的坐标为( )
A、9:15 B、9:20 C、9:25 D、9:3011. 如图,在 中, , ,点 在边 上,且 ,点 为 的中点,点 为边 上的动点,当点 在 上移动时,使四边形 周长最小的点 的坐标为( )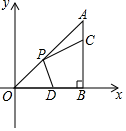 A、 B、 C、 D、12. 如图是函数 的图象,直线 轴且过点 ,将该函数在直线l上方的图象沿直线l向下翻折,在直线1下方的图象保持不变,得到一个新图象.若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是( )
A、 B、 C、 D、12. 如图是函数 的图象,直线 轴且过点 ,将该函数在直线l上方的图象沿直线l向下翻折,在直线1下方的图象保持不变,得到一个新图象.若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是( ) A、 B、 C、 D、 或
A、 B、 C、 D、 或二、填空题
-
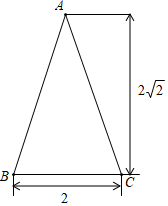
13. 计算: = .14. 如图是一个圆锥的主视图,根据图中标出的数据(单位: ),计算这个圆锥侧面展开图圆心角的度数为 .
 15. 为了了解某区初中学生的视力情况,随机抽取了该区500名初中学生进行调查.整理样本数据,得到下表:
15. 为了了解某区初中学生的视力情况,随机抽取了该区500名初中学生进行调查.整理样本数据,得到下表:视力
4.7以下
4.7
4.8
4.9
4.9以上
人数
102
98
80
93
127
根据抽样调查结果,估计该区12000名初中学生视力不低于4.8的人数是.
16. a是方程 的一个根,则代数式 的值是 .17. 在△ABC中,AB=4,∠C=60°,∠A>∠B,则BC的长的取值范围是.18. 给出以下命题:①平分弦的直径垂直于这条弦;②已知点 、 、 均在反比例函数 的图象上,则 ;③若关于x的不等式组 无解,则 ;④将点 向左平移3个单位到点 ,再将 绕原点逆时针旋转90°到点 ,则 的坐标为 .其中所有真命题的序号是 .
三、解答题
-
19. 计算: .20. 为了解“哈啰单车”的使用情况,小月对部分用户的骑行时间t(分)进行了随机抽查,将获得的数据分成四组(A: ;B: ;C: ;D: ),并绘制出如图所示的两幅不完整的统计图.
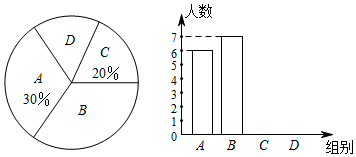 (1)、求D组所在扇形的圆心角的度数,并补全条形统计图;(2)、小月打算在C、D两组中各随机选一名用户进行采访,若这两组中各有两名女士,请用列表或画树状图的方法求出恰好选中一男一女的概率.21. 如图,在平行四边形ABCD中,对角线AC与BD交于点O,点M,N分别为OA、OC的中点,延长BM至点E,使 ,连接DE.
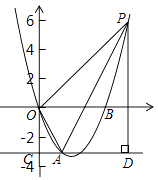
(1)、求D组所在扇形的圆心角的度数,并补全条形统计图;(2)、小月打算在C、D两组中各随机选一名用户进行采访,若这两组中各有两名女士,请用列表或画树状图的方法求出恰好选中一男一女的概率.21. 如图,在平行四边形ABCD中,对角线AC与BD交于点O,点M,N分别为OA、OC的中点,延长BM至点E,使 ,连接DE. (1)、求证: ;(2)、若 ,且 , ,求四边形DEMN的面积.22. 为了参加西部博览会,资阳市计划印制一批宣传册.该宣传册每本共10页,由A、B两种彩页构成.已知A种彩页制版费300元/张,B种彩页制版费200元/张,共计2400元.(注:彩页制版费与印数无关)(1)、每本宣传册A、B两种彩页各有多少张?(2)、据了解,A种彩页印刷费2.5元/张,B种彩页印刷费1.5元/张,这批宣传册的制版费与印刷费的和不超过30900元.如果按到资阳展台处的参观者人手一册发放宣传册,预计最多能发给多少位参观者?23. 如图,点 , 是直线 与反比例函数 图象的两个交点, 轴,垂足为点 ,已知 ,连接 , , .
(1)、求证: ;(2)、若 ,且 , ,求四边形DEMN的面积.22. 为了参加西部博览会,资阳市计划印制一批宣传册.该宣传册每本共10页,由A、B两种彩页构成.已知A种彩页制版费300元/张,B种彩页制版费200元/张,共计2400元.(注:彩页制版费与印数无关)(1)、每本宣传册A、B两种彩页各有多少张?(2)、据了解,A种彩页印刷费2.5元/张,B种彩页印刷费1.5元/张,这批宣传册的制版费与印刷费的和不超过30900元.如果按到资阳展台处的参观者人手一册发放宣传册,预计最多能发给多少位参观者?23. 如图,点 , 是直线 与反比例函数 图象的两个交点, 轴,垂足为点 ,已知 ,连接 , , .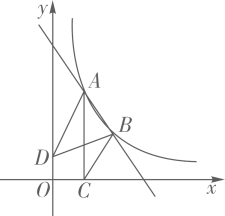 (1)、求直线 的表达式;(2)、 和 的面积分别为 , ,求 .
(1)、求直线 的表达式;(2)、 和 的面积分别为 , ,求 .