四川省达州市2023年中考二模数学试题
试卷更新日期:2023-05-18 类型:中考模拟
一、单选题
-
1. 的倒数的绝对值是( )A、2023 B、 C、 D、2. 下面的几何体中,主视图不是矩形的是( )A、
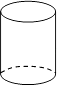 B、
B、 C、
C、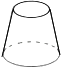 D、
D、 3. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有克,将数用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 已知三角形的两条边长分别为4和6,那么顺次连接该三角形三边中点所得三角形的周长可能是( )A、12 B、10 C、8 D、66. 若x=-2是关于x的一元二次方程x2+ ax-a2=0的一个根,则a的值为( )A、1或-4 B、-1或-4 C、-1或4 D、1或47. 为了某小区居民的用水情况,随机抽查了10户家庭的月用水量,结果如下表:
3. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有克,将数用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 已知三角形的两条边长分别为4和6,那么顺次连接该三角形三边中点所得三角形的周长可能是( )A、12 B、10 C、8 D、66. 若x=-2是关于x的一元二次方程x2+ ax-a2=0的一个根,则a的值为( )A、1或-4 B、-1或-4 C、-1或4 D、1或47. 为了某小区居民的用水情况,随机抽查了10户家庭的月用水量,结果如下表:月用水量(吨)
4
5
6
9
户数
3
4
2
1
则关于这10户家庭的约用水量,下列说法错误的是( )
A、中位数是5吨 B、极差是3吨 C、平均数是5.3吨 D、众数是5吨8. 抛物线 的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为 ,则b、c的值为( )A、b=2,c=﹣6 B、b=2,c=0 C、b=﹣6,c=8 D、b=﹣6,c=29. 如图,已知点在函数位于第二象限的图像上,点在函数位于第一象限的图像上,点在y轴的正半轴上,若四边形都是正方形,则正方形的边长为( )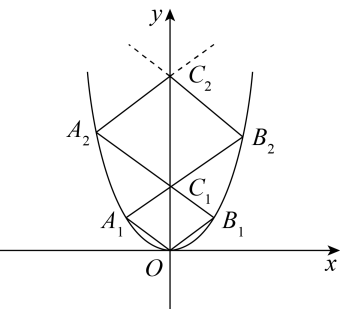 A、1012 B、 C、 D、10. 已知二次函数的图象如图所示,有下列5个结论:(1);(2);(3);(4);(5)(的实数);其中正确的结论有( )
A、1012 B、 C、 D、10. 已知二次函数的图象如图所示,有下列5个结论:(1);(2);(3);(4);(5)(的实数);其中正确的结论有( )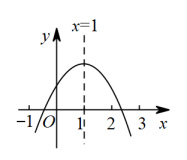 A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
11. 已知a2+3a=1,则代数式2a2+6a﹣1的值为 .12. 在一不透明的袋子里装有除颜色外完全相同的4个红色小球和绿色小球若干个,若从袋中随机摸出一个小球是红色的概率为 , 则袋子里装有个绿色小球.13. 如图,在 中, ,底边 ,线段AB的垂直平分线交BC于点E,则 的周长为.
 14. 如图,点A在双曲线y=的第一象限的那一支上,AB垂直于y轴与点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为 .
14. 如图,点A在双曲线y=的第一象限的那一支上,AB垂直于y轴与点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为 .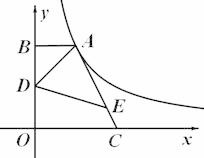 15. 如图,△ABC是⊙O内接正三角形,将△ABC绕点O顺时针旋转30°得到△DEF,DE分别交AB,AC于点M,N,DF交AC于点Q,则有以下结论:①∠DQN=30°;②△DNQ≌△ANM;③△DNQ的周长等于AC的长;④NQ=QC.其中正确的结论是 . (把所有正确的结论的序号都填上)
15. 如图,△ABC是⊙O内接正三角形,将△ABC绕点O顺时针旋转30°得到△DEF,DE分别交AB,AC于点M,N,DF交AC于点Q,则有以下结论:①∠DQN=30°;②△DNQ≌△ANM;③△DNQ的周长等于AC的长;④NQ=QC.其中正确的结论是 . (把所有正确的结论的序号都填上)
三、解答题
-
16.(1)、计算: .(2)、已知方程有实数根,求m的取值范围.17. 我市某中学为备战省运会,在校运动队的学生中进行了全能选手的选拔,并将参加选拔学生的综合成绩分成四组,绘成了如下尚不完整的统计图表.
组别
成绩
组中值
频数
第一组
95
4
第二组
85
m
第三组
75
n
第四组
65
21
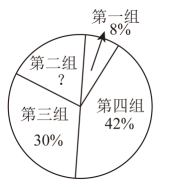
根据图表信息,回答下列问题:
(1)、参加活动选拔的学生共有人;表中 , .(2)、将第一组中的4名学生记为A、B、C、D,由于这4名学生的体育综合水平相差不大,现决定随机挑选其中两名学生代表学校参赛,试通过画树形图或列表的方法求恰好选中A和B的概率.18. 如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1: , 且AB=26米.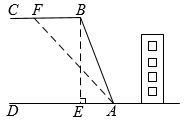 (1)、求坡顶与地面的距离BE的长.(2)、为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡.学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33).19. 在如图的方格纸中(每个小方格的边长都是1个单位)有一个格点 ,
(1)、求坡顶与地面的距离BE的长.(2)、为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡.学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33).19. 在如图的方格纸中(每个小方格的边长都是1个单位)有一个格点 , (1)、求出的边长,并判断的形状;(2)、作出关于点O的中心对称图形;作出绕点O按顺时针方向旋转后得到的图形;(3)、可能由怎样变换得到?(写出你认为正确的一种即可).20. 如图,在梯形中, , 点E在上,且 ,
(1)、求出的边长,并判断的形状;(2)、作出关于点O的中心对称图形;作出绕点O按顺时针方向旋转后得到的图形;(3)、可能由怎样变换得到?(写出你认为正确的一种即可).20. 如图,在梯形中, , 点E在上,且 ,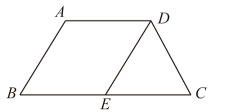 (1)、试判断四边形ABED的形状,并说明理由;(2)、若 , ,
(1)、试判断四边形ABED的形状,并说明理由;(2)、若 , ,①求的度数;
②当时,求四边形ABED的面积.
21. 某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示: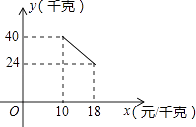 (1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?(3)、该经销商想要每天获得150元的销售利润,销售价应定为多少?22. 为的内接三角形,P为延长线上一点, , 为的直径,过C作交于E,交于F,交于 .
(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?(3)、该经销商想要每天获得150元的销售利润,销售价应定为多少?22. 为的内接三角形,P为延长线上一点, , 为的直径,过C作交于E,交于F,交于 .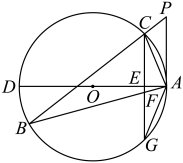 (1)、判断直线与的位置关系,并说明理由;(2)、求证: .23. 使得函数值为零的自变量的值称为函数的零点.例如,对于函数 , 令y=0,可得x=1,我们就说1是函数的零点.
(1)、判断直线与的位置关系,并说明理由;(2)、求证: .23. 使得函数值为零的自变量的值称为函数的零点.例如,对于函数 , 令y=0,可得x=1,我们就说1是函数的零点.已知函数(m为常数).
(1)、当=0时,求该函数的零点;(2)、证明:无论m取何值,该函数总有两个零点;(3)、设函数的两个零点分别为和 , 且 , 此时函数图象与x轴的交点分别为A、B(点A在点B左侧),点M在直线上,当MA+MB最小时,求直线AM的函数解析式.24. 如图,二次函数y=ax2+bx+c的图象的顶点C的坐标为(0,﹣2),交x轴于A、B两点,其中A(﹣1,0),直线l:x=m(m>1)与x轴交于D.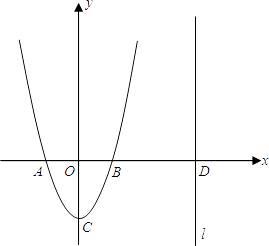 (1)、求二次函数的解析式和B的坐标;(2)、在直线l上找点P(P在第一象限),使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似,求点P的坐标(用含m的代数式表示);(3)、在(2)成立的条件下,在抛物线上是否存在第一象限内的点Q,使△BPQ是以P为直角顶点的等腰直角三角形?如果存在,请求出点Q的坐标;如果不存在,请说明理由.25. 如图1,在中,把绕点A顺时针旋转()得到 , 把绕点A逆时针旋转得到 , 连接 . 当时,我们称是的“旋补三角形”,边上的中线叫做的“旋补中线”,点A叫做“旋补中心”.
(1)、求二次函数的解析式和B的坐标;(2)、在直线l上找点P(P在第一象限),使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似,求点P的坐标(用含m的代数式表示);(3)、在(2)成立的条件下,在抛物线上是否存在第一象限内的点Q,使△BPQ是以P为直角顶点的等腰直角三角形?如果存在,请求出点Q的坐标;如果不存在,请说明理由.25. 如图1,在中,把绕点A顺时针旋转()得到 , 把绕点A逆时针旋转得到 , 连接 . 当时,我们称是的“旋补三角形”,边上的中线叫做的“旋补中线”,点A叫做“旋补中心”.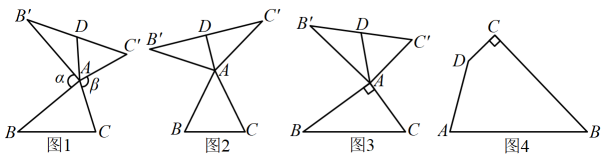 (1)、在图2,图3中,是的“旋补三角形”,是的“旋补中线”.
(1)、在图2,图3中,是的“旋补三角形”,是的“旋补中线”.①如图2,当为等边三角形时,与的数量关系为;
②如图3,当 , 时,则长为 .
(2)、在图1中,当为任意三角形时,猜想与的数量关系,并给予证明.(3)、如图4,在四边形 , , , , , , 在四边形内部是否存在点P,使是的“旋补三角形”?若存在,给予证明,并求的“旋补中线”长;若不存在,说明理由.