四川省成都市武侯区2023年中考数学二模试题
试卷更新日期:2023-05-18 类型:中考模拟
一、单选题
-
1. 下列各数中,倒数是它本身的数是( )A、1 B、0 C、2 D、2. 近两年新能源汽车比亚迪的销量实现了快速增长,2023年比亚迪计划冲击400万台的整车年度销量目标.将数据400万用科学记数法表示为( )A、 B、 C、 D、3. 若分式有意义,则x的取值范围是( )A、 B、 C、 D、4. 成都市武侯区“水韵园”综合教育基地设有民族危机档案、科技创想营地、匠心制作工坊、舒心交流空间、时尚体育时分五大教育功能区,某校组织学生分区体验种类丰富、课程新颖的综合实践活动.每个功能区的人数分别为:80,79,82,81,82.则这组数据的中位数和众数分别是( ).A、80,81 B、81,81 C、79,82 D、81,825. 不等式组的解集在数轴上表示正确的是( )A、
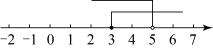 B、
B、 C、
C、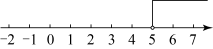 D、
D、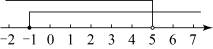 6. 若m,n满足 , 则的值为( )A、 B、1 C、 D、27. 在平面直角坐标系中,将点先向左平移3个单位长度,再向上平移2个单位长度,则平移后的点的坐标是( )A、 B、 C、 D、8. 如图,在中,分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N,作直线MN交边AB于点D.若 , , 则的度数为( )
6. 若m,n满足 , 则的值为( )A、 B、1 C、 D、27. 在平面直角坐标系中,将点先向左平移3个单位长度,再向上平移2个单位长度,则平移后的点的坐标是( )A、 B、 C、 D、8. 如图,在中,分别以点A和C为圆心,以大于的长为半径作弧,两弧相交于点M和N,作直线MN交边AB于点D.若 , , 则的度数为( )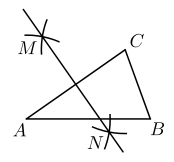 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
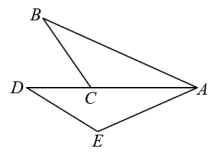
9. 因式分解: = .10. 如图,将绕着点A逆时针旋转得到 , 使得点B的对应点D落在边的延长线上,若 , , 则线段的长为 .
 11. 已知关于的一元二次方程有两个相等的实数根,则 .12. 如图,在平面直角坐标系中,菱形的顶点B在x轴的负半轴上,顶点C在x轴的正半轴上,顶点D在y轴上,若点A的坐标是 , 则点C的坐标是 .
11. 已知关于的一元二次方程有两个相等的实数根,则 .12. 如图,在平面直角坐标系中,菱形的顶点B在x轴的负半轴上,顶点C在x轴的正半轴上,顶点D在y轴上,若点A的坐标是 , 则点C的坐标是 .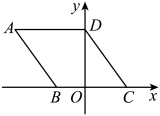 13. 在二次函数的图象上有 , 两点,若 , 则a的取值范围是 .
13. 在二次函数的图象上有 , 两点,若 , 则a的取值范围是 .三、解答题
-
14.(1)、计算: .(2)、解方程组:15. 2023年7月28日至8月8日,第31届世界大学生夏季运动会将在成都举行(以下简称“成都大运会”),这是成都第一次举办世界性综合运动会.某校为了解同学们对“成都大运会”竞赛项目的知晓情况,对部分同学进行了随机抽样调查,结果分为四种类型:A.非常了解;B.比较了解;C.基本了解;D.不了解,并将调查结果绘制成如下两幅不完整的统计图表.
知晓情况
人数
A.非常了解
4
B.比较了解
18
C.基本了解
m
D.不了解
5
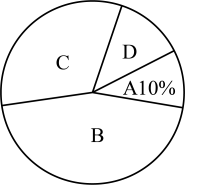
根据图表信息,解答下列问题:
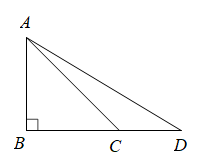
(1)、求本次调查的总人数及表中m的值;(2)、求扇形统计图中“C”对应的扇形圆心角的度数;(3)、“非常了解”的四名同学分别是 , 两名女生, , 两名男生,若从中随机选取两名同学向全校作交流,请利用画树状图或列表的方法,求恰好选到一名男生和一名女姓的概率.16. 成都凤凰山体育公园由“一场两馆”组成,其中“一场”指的是按照FIFA标准建设的专业足球场,配备专业的固草系统,能同时容纳6万名观众.某数学兴趣小组利用所学知识测量该足球场所在建筑物的高度.如图,他们先在地面C处测得建筑物的顶部A的仰角 , 又在与C相距43米的D处测得建筑物的顶部A的仰角(其中点B,C,D在同一条直线上),求建筑物的高度.(结果精确到米;参考数据: , )
 17. 如图,为的直径,C,D为上两点,连接 , , , , 线段与相交于点E,过点D作 , 交的延长线于点F.
17. 如图,为的直径,C,D为上两点,连接 , , , , 线段与相交于点E,过点D作 , 交的延长线于点F. (1)、求证:是的切线;(2)、若 , , , 求的半径.18. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于 , 两点.
(1)、求证:是的切线;(2)、若 , , , 求的半径.18. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于 , 两点.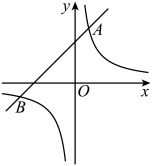 (1)、分别求一次函数及反比例函数的表达式;(2)、在第三象限内的B点右侧的反比例函数图象上取一点P,连接且满足 .
(1)、分别求一次函数及反比例函数的表达式;(2)、在第三象限内的B点右侧的反比例函数图象上取一点P,连接且满足 .i)求点P的坐标;
ii)过点A作直线 , 在直线l上取一点Q,且点Q位于点A的左侧,连接 , 试问:能否与相似?若能,求出此时点Q的坐标;若不能,请说明理由.
四、填空题
-
19. 我们常用一个大写字母来表示一个代数式,已知 , , 则化简的结果为 .20. 当今大数据时代,“二维码”广泛应用于我们的日常生活中,某兴趣小组从某个二维码中截取部分开展数学实验活动.如图,在边长为的正方形区域内通过计算机随机掷点,经过大量重复实验,发现点落在区域内黑色部分的频率稳定在左右,据此可以估计这个区域内白色部分的总面积约为 .
 21. 已知P是内一点(点P不与圆心O重合),点P到圆上各点的距离中,最小距离与最大距离是关于x的一元二次方程的两个实数根,则的直径为 .22. 在等边中(其中),点P在边上运动,点Q在边上运动,且满足(点P,Q都不与B重合),以为底边在左侧做等腰三角形 , 使得 . 则四边形的面积的最大值是 .
21. 已知P是内一点(点P不与圆心O重合),点P到圆上各点的距离中,最小距离与最大距离是关于x的一元二次方程的两个实数根,则的直径为 .22. 在等边中(其中),点P在边上运动,点Q在边上运动,且满足(点P,Q都不与B重合),以为底边在左侧做等腰三角形 , 使得 . 则四边形的面积的最大值是 .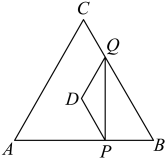 23. 某投球发射装置斜向上发射进行投球实验,球离地面的高度h(米)与球运行时间t(秒)之间满足函数关系式 , 该装置的发射点离地面10米,球筐中心点离地面35米.如图,若某次投球正好中心入筐,球到达球筐中心点所需时间为5秒,那么这次投球过程中球离地面的高度h(米)与球运行时间t(秒)之间满足的函数关系式为 . (不要求写自变量的取值范围);我们把球在每2秒内运行的最高点离地面的高度与最低点离地面的高度的差称为“投射矩”,常用字母“L”表示.那么在这次投球过程中,球入筺前L的取值范围是 .
23. 某投球发射装置斜向上发射进行投球实验,球离地面的高度h(米)与球运行时间t(秒)之间满足函数关系式 , 该装置的发射点离地面10米,球筐中心点离地面35米.如图,若某次投球正好中心入筐,球到达球筐中心点所需时间为5秒,那么这次投球过程中球离地面的高度h(米)与球运行时间t(秒)之间满足的函数关系式为 . (不要求写自变量的取值范围);我们把球在每2秒内运行的最高点离地面的高度与最低点离地面的高度的差称为“投射矩”,常用字母“L”表示.那么在这次投球过程中,球入筺前L的取值范围是 .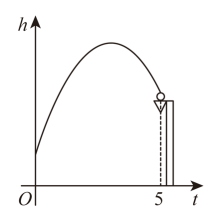
五、解答题
-
24. 文明,是一座城市的幸福底色,是城市的内在气质.2023年是成都争创全国文明典范城市的关键之年.为积极推进创建工作,某社区计划购买A,B两种型号的垃圾分装桶共120个,其中A型垃圾分装桶的个数不少于B型的一半.根据市场调查,A型垃圾分装桶的价格为每个400元,B型垃圾分装桶的价格为每个100元.
 (1)、设购买A型垃圾分装桶x个,求x的取值范围;(2)、某企业为了更好地服务于社区,打算捐赠这批垃圾分装桶,试问:该企业最少需要花费多少元?25. 如图,在平面直角坐标系中,直线分别与x轴,y轴相交于A,B两点,抛物线经过点A,点C是抛物线的顶点,连接 .
(1)、设购买A型垃圾分装桶x个,求x的取值范围;(2)、某企业为了更好地服务于社区,打算捐赠这批垃圾分装桶,试问:该企业最少需要花费多少元?25. 如图,在平面直角坐标系中,直线分别与x轴,y轴相交于A,B两点,抛物线经过点A,点C是抛物线的顶点,连接 .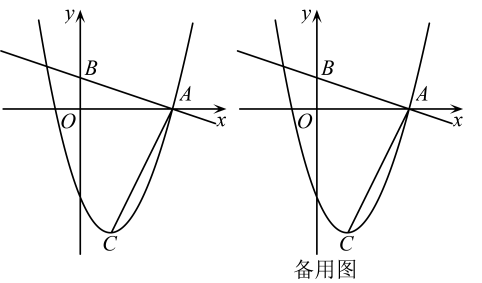 (1)、求抛物线的函数表达式及顶点C的坐标;(2)、求的度数;(3)、设直线与抛物线相交于P,Q两点(点P在点Q的左侧),当直线与直线相交所成的一个角为时,求点Q的坐标.26. 如图1,在矩形中,(其中),点P是边上一动点(点P不与A重合),点E是边的中点,连接 , 将矩形沿直线进行翻折,其顶点A翻折后的对应点为O,连接并延长,交边于点F(点F不与C重合),过点F作的平分线 , 交矩形的边于点G.
(1)、求抛物线的函数表达式及顶点C的坐标;(2)、求的度数;(3)、设直线与抛物线相交于P,Q两点(点P在点Q的左侧),当直线与直线相交所成的一个角为时,求点Q的坐标.26. 如图1,在矩形中,(其中),点P是边上一动点(点P不与A重合),点E是边的中点,连接 , 将矩形沿直线进行翻折,其顶点A翻折后的对应点为O,连接并延长,交边于点F(点F不与C重合),过点F作的平分线 , 交矩形的边于点G.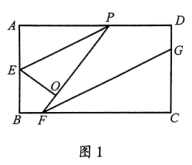
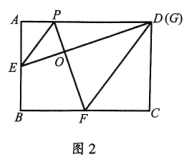
 (1)、求证:;(2)、如图2,在点P运动过程中,若E,O,G三点在同一条直线上时,点G与点D刚好重合,求n的值;(3)、若 , 连接 , , 当是以为直角边的直角三角形时,求的值.
(1)、求证:;(2)、如图2,在点P运动过程中,若E,O,G三点在同一条直线上时,点G与点D刚好重合,求n的值;(3)、若 , 连接 , , 当是以为直角边的直角三角形时,求的值.