陕西省渭南市澄城县2023年中考数学一模试卷
试卷更新日期:2023-05-18 类型:中考模拟
一、单选题
-
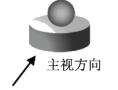
1. 若点在反比例函数的图像上,则a的值为( )A、 B、 C、 D、2. 如图所示几何体是由一个球体和一个圆柱组成的,它的俯视图是( )
 A、
A、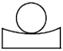 B、
B、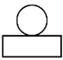 C、
C、 D、
D、 3. 若二次函数的图象经过点 , , 则关于x的方程的解为( )A、 , B、 , C、 , D、 ,4. 某小组做“用频率估计概率”的实验时,绘出的某一结果出现的频率分布折线图,则符合这一结果的实验可能是( )
3. 若二次函数的图象经过点 , , 则关于x的方程的解为( )A、 , B、 , C、 , D、 ,4. 某小组做“用频率估计概率”的实验时,绘出的某一结果出现的频率分布折线图,则符合这一结果的实验可能是( )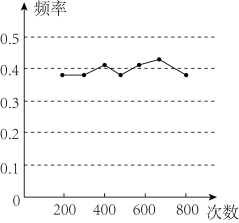 A、抛一枚均匀硬币,出现正面朝上 B、掷一个正六面体的骰子,出现2点朝上 C、从一个装有3个红球2个黑球的袋子中任取一球,取到的是黑球 D、一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃5. 已知两个相似三角形的面积之比为4:9,这两个三角形的周长的和是 , 那么较小的三角形的周长为( )A、 B、 C、 D、6. 如图,在中, , , 的垂直平分线交于点D,连接 , 若 , 则的长为( )
A、抛一枚均匀硬币,出现正面朝上 B、掷一个正六面体的骰子,出现2点朝上 C、从一个装有3个红球2个黑球的袋子中任取一球,取到的是黑球 D、一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃5. 已知两个相似三角形的面积之比为4:9,这两个三角形的周长的和是 , 那么较小的三角形的周长为( )A、 B、 C、 D、6. 如图,在中, , , 的垂直平分线交于点D,连接 , 若 , 则的长为( )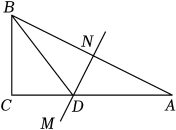 A、 B、 C、 D、7. 如图,是的直径,点A是外一点,连接交于点E,连接并延长交于点D,若 , 则的度数是( )
A、 B、 C、 D、7. 如图,是的直径,点A是外一点,连接交于点E,连接并延长交于点D,若 , 则的度数是( )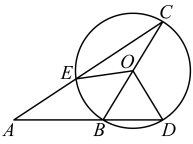 A、 B、 C、 D、8. 在平面直角坐标系中,有两条抛物线关于x轴对称,且他们的顶点相距6个单位长度,若其中一条抛物线的解析式为 , 则m的值是( )
A、 B、 C、 D、8. 在平面直角坐标系中,有两条抛物线关于x轴对称,且他们的顶点相距6个单位长度,若其中一条抛物线的解析式为 , 则m的值是( )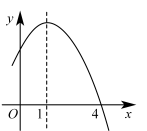 A、 B、 C、或 D、或
A、 B、 C、或 D、或二、填空题
-
9. 已知是关于x的方程的一个根,则m的值为 .10. 如图, 、 、 、 为一个正多边形的顶点, 为正多边形的中心,若 ,则这个正多边形的边数为.
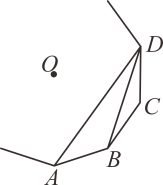 11. 在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比(即),可以增加视觉美感.如图,按此比例设计一座高度为的雕像,则该雕像的下部高度应设计为 m.(结果保留根号)
11. 在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比(即),可以增加视觉美感.如图,按此比例设计一座高度为的雕像,则该雕像的下部高度应设计为 m.(结果保留根号) 12. 如图,点A是反比例函数图象上一点,轴于点C,与反比例函数的图象交于点B, , 连接 , 若的面积为2,则 .
12. 如图,点A是反比例函数图象上一点,轴于点C,与反比例函数的图象交于点B, , 连接 , 若的面积为2,则 .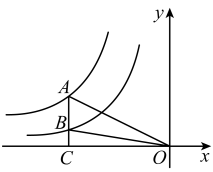 13. 如图,在矩形中, , 连接 , 将线段绕着点A顺时针旋转得到 , 则线段的最小值为 .
13. 如图,在矩形中, , 连接 , 将线段绕着点A顺时针旋转得到 , 则线段的最小值为 .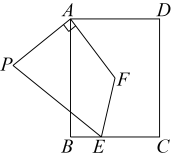
三、解答题
-
14. 计算:15. 已知一元二次方程的两个根分别为m,n,求的值.16. 如图,在平面直角坐标系中,每个小正方形的边长均为1,的顶点均在网格格点上,且 , , .
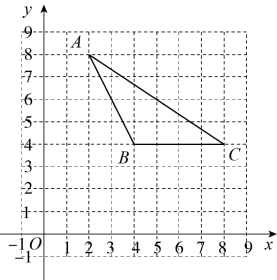 (1)、以原点O为位似中心,在第一象限画出 , 使得与位似,且与的相似比 , 点A、B、C的对应点分别为点、、;(2)、点的坐标为 .17. 如图,在中, , 点D在上,连接 , 利用尺规作图法求作 , 使经过点B、C、D.(不写作法,保留作图痕迹)
(1)、以原点O为位似中心,在第一象限画出 , 使得与位似,且与的相似比 , 点A、B、C的对应点分别为点、、;(2)、点的坐标为 .17. 如图,在中, , 点D在上,连接 , 利用尺规作图法求作 , 使经过点B、C、D.(不写作法,保留作图痕迹)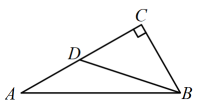 18. 如图,点E,F分别在正方形ABCD的边BC,CD上,且 . 把绕点A顺时针旋转得到 . 求证: .
18. 如图,点E,F分别在正方形ABCD的边BC,CD上,且 . 把绕点A顺时针旋转得到 . 求证: . 19. 随着环保意识日益深入,我国新能源汽车的生产技术也不断提升.市场上某款新能源汽车1月份的售价为25万元/辆,3月份下降到20.25万元/辆,求该款汽车售价的月平均下降率.20. 中国古代有很多辉煌的数学成就,《周髀算经》《九章算术》《海岛算经》等都是我国古代数学的重要文献.某数学兴趣小组准备采用抽签的方式确定学习内容,将书目制成编号为A,B,C的3张卡片(如图所示,卡片除编号和书目外,其余完全相同).现将这3张卡片背面朝上,洗匀放好.
19. 随着环保意识日益深入,我国新能源汽车的生产技术也不断提升.市场上某款新能源汽车1月份的售价为25万元/辆,3月份下降到20.25万元/辆,求该款汽车售价的月平均下降率.20. 中国古代有很多辉煌的数学成就,《周髀算经》《九章算术》《海岛算经》等都是我国古代数学的重要文献.某数学兴趣小组准备采用抽签的方式确定学习内容,将书目制成编号为A,B,C的3张卡片(如图所示,卡片除编号和书目外,其余完全相同).现将这3张卡片背面朝上,洗匀放好. (1)、从3张卡片中随机抽取1张,求抽到《周髀算经》的概率;(2)、若甲同学从3张卡片中随机抽取1张后放回洗匀,乙同学再从3张卡片中随机抽取1张,请用列表或画树状图的方法,求甲乙两位同学抽中不同书目的概率.21. 位于陕西省渭南市澄城县城以南6公里处的印象古徵民俗文化园将现代都市生活与田园乡村气息完美结合,原汁原味的关中民俗风情诱惑着一批又一批的人前来游览.某个天气晴好的周末,欢欢和乐乐两个人去印象古徵民俗文化园游玩,看见园中的一棵大树,于是他们想运用所学知识测量这棵树的高度.如图,乐乐站在大树的影子的末端C处,同一时刻,欢欢在乐乐的影子的末端E处做上标记,随后两人用尺子测得米,米.已知乐乐的身高米,B、C、E在一条直线上, , . 请你运用所学知识,帮助欢欢和乐乐求出这棵大树的高度 .
(1)、从3张卡片中随机抽取1张,求抽到《周髀算经》的概率;(2)、若甲同学从3张卡片中随机抽取1张后放回洗匀,乙同学再从3张卡片中随机抽取1张,请用列表或画树状图的方法,求甲乙两位同学抽中不同书目的概率.21. 位于陕西省渭南市澄城县城以南6公里处的印象古徵民俗文化园将现代都市生活与田园乡村气息完美结合,原汁原味的关中民俗风情诱惑着一批又一批的人前来游览.某个天气晴好的周末,欢欢和乐乐两个人去印象古徵民俗文化园游玩,看见园中的一棵大树,于是他们想运用所学知识测量这棵树的高度.如图,乐乐站在大树的影子的末端C处,同一时刻,欢欢在乐乐的影子的末端E处做上标记,随后两人用尺子测得米,米.已知乐乐的身高米,B、C、E在一条直线上, , . 请你运用所学知识,帮助欢欢和乐乐求出这棵大树的高度 .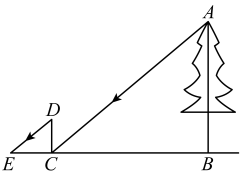 22. 某商店销售一款工艺品,每件成本为元,为了合理定价,投放市场进行试销.据市场调查,销售单价是元时,每月的销售量是件,而销售单价每降价元,每月可多销售件.设这种工艺品每件降价x元.(1)、每件工艺品的实际利润为元(用含有x的式子表示);(2)、为达到每月销售这种工艺品的利润为元,且要求降价不超过元,那么每件工艺品应降价多少元?23. 某广场举行无人机表演,如图,点处各有一架无人机,它们在同一水平线上,与地面的距离为 . 此时,点E到点A处的俯角为 , 点E到点C处的俯角为 , 点D到点C处的俯角为 , 点A到点C处的仰角为 . 点均在同一平面内,求两架无人机之间的距离的长.(结果保留根号)
22. 某商店销售一款工艺品,每件成本为元,为了合理定价,投放市场进行试销.据市场调查,销售单价是元时,每月的销售量是件,而销售单价每降价元,每月可多销售件.设这种工艺品每件降价x元.(1)、每件工艺品的实际利润为元(用含有x的式子表示);(2)、为达到每月销售这种工艺品的利润为元,且要求降价不超过元,那么每件工艺品应降价多少元?23. 某广场举行无人机表演,如图,点处各有一架无人机,它们在同一水平线上,与地面的距离为 . 此时,点E到点A处的俯角为 , 点E到点C处的俯角为 , 点D到点C处的俯角为 , 点A到点C处的仰角为 . 点均在同一平面内,求两架无人机之间的距离的长.(结果保留根号)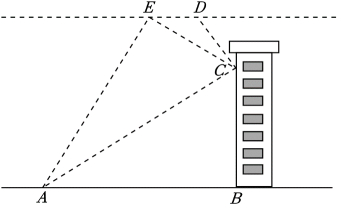 24. 如图,是的外接圆,且 , 点M是的中点,作交的延长线于点N,连接交于点D.
24. 如图,是的外接圆,且 , 点M是的中点,作交的延长线于点N,连接交于点D.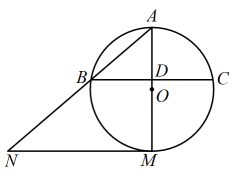 (1)、求证:是的切线;(2)、若 , 求的半径.25. 如图,抛物线与x轴交于点、B,与y轴交于点 , 直线l是抛物线的对称轴.
(1)、求证:是的切线;(2)、若 , 求的半径.25. 如图,抛物线与x轴交于点、B,与y轴交于点 , 直线l是抛物线的对称轴.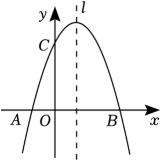 (1)、求抛物线的函数解析式;(2)、在对称轴l上是否存在点M,使为等腰三角形,若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.26. 【问题情景】
(1)、求抛物线的函数解析式;(2)、在对称轴l上是否存在点M,使为等腰三角形,若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.26. 【问题情景】含角的直角三角板中 . 将其绕直角顶点C顺时针旋转α角 , 得到 , 边与边AB交于点D.
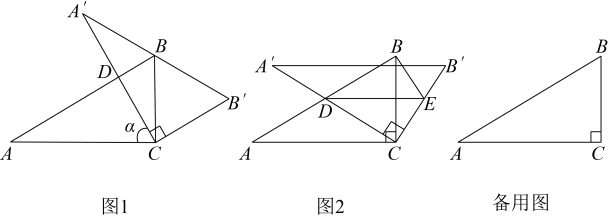 (1)、如图1,若边经过点B,则α的度数为°;(2)、【探究发现】
(1)、如图1,若边经过点B,则α的度数为°;(2)、【探究发现】如图2是旋转过程的一个位置,过点D作交边于点E,连接 , 小明发现在三角板旋转的过程中,度数是定值,求的度数;
(3)、【拓展延伸】在(2)的条件下,设 , 的面积为S,当时,
①求的长;
②以点E为圆心,为半径作 , 并判断此时直线与的位置关系.