陕西省宝鸡市扶风县2023年中考数学一模试卷
试卷更新日期:2023-05-18 类型:中考模拟
一、单选题
-
1. -3的绝对值是( )A、3 B、 C、 D、2. 如图,直线 , 的直角顶点A落在直线a上,点B落在直线b上,若 , , 则的大小为( )
 A、 B、 C、 D、3. 按照如图所示的运算程序,下列输入的数据中,能使输出的结果为9的是( )
A、 B、 C、 D、3. 按照如图所示的运算程序,下列输入的数据中,能使输出的结果为9的是( ) A、 B、 C、 D、4. 如图,在中,和的平分线相交于点D,若 , 则的度数为( )
A、 B、 C、 D、4. 如图,在中,和的平分线相交于点D,若 , 则的度数为( ) A、 B、 C、 D、5. 如图,点E为菱形的边BC上一点,且 , 连接与对角线相交于点F.已知 , 则的长为( )
A、 B、 C、 D、5. 如图,点E为菱形的边BC上一点,且 , 连接与对角线相交于点F.已知 , 则的长为( )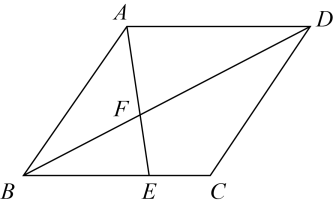 A、4 B、5 C、6 D、86. 已知一次函数的图象与x轴交于点A,与y轴交于点 , 且y随着x的增大而减小,则点A的坐标为( )A、 B、 C、 D、7. 如图,是的直径,C、D是上的两点,且点C为弧的中点,连接、、 . 若 , 则的度数为( )
A、4 B、5 C、6 D、86. 已知一次函数的图象与x轴交于点A,与y轴交于点 , 且y随着x的增大而减小,则点A的坐标为( )A、 B、 C、 D、7. 如图,是的直径,C、D是上的两点,且点C为弧的中点,连接、、 . 若 , 则的度数为( )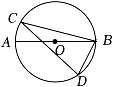 A、 B、 C、 D、8. 若抛物线M:与抛物线:关于直线对称,则m,n的值分别为( )A、 , B、 , C、 , D、 ,
A、 B、 C、 D、8. 若抛物线M:与抛物线:关于直线对称,则m,n的值分别为( )A、 , B、 , C、 , D、 ,二、填空题
-
9. 比较大小:(填“>”或“<”).10. 一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .11. 如图所示△ABC和△A'B'C'是以点O为位似中心的位似图形,已知点C'是OC的三等分点,则△A'B'C'与△ABC的面积之比为 .
 12. 已知正比例函数与反比例函数的图象交于点和点B,则点B的坐标是 .13. 如图,在四边形ABCD中,CD=1,AB=2BC= , 且∠ABC+∠BCD=225°,则四边形ABCD周长的最大值为 .
12. 已知正比例函数与反比例函数的图象交于点和点B,则点B的坐标是 .13. 如图,在四边形ABCD中,CD=1,AB=2BC= , 且∠ABC+∠BCD=225°,则四边形ABCD周长的最大值为 .
三、解答题
-
14. 计算: .15. 解方程组: .16. 化简: .17. 如图,是的角平分线,请用尺规作图法求作的内心.(保留作图痕迹,不写作法).
 18. 如图,点C,D在线段上, , , .
18. 如图,点C,D在线段上, , , .求证: .
 19. 如图,在平面直角坐标系中,的顶点均在网格的格点上,其坐标分别为: .
19. 如图,在平面直角坐标系中,的顶点均在网格的格点上,其坐标分别为: . (1)、在图中作出关于x轴对称的;(2)、在(1)的条件下,分别写出点A、C的对应点、的坐标.20. 热情的刘老师邀请两位朋友茗茗和欣欣来西安游玩,他向两人推荐了四个游览地:兵马俑、西安城墙、华清宫和陕西省历史博物馆,并制作了四个外形完全一致的纸签,纸签上分别写有这四个游览地,让两位朋友随机抽取.抽签规则为:茗茗先抽签,放回洗匀后,再由欣欣抽签,(1)、茗茗抽取到“兵马俑”的概率为;(2)、请用树状图或列表法求两人抽取到同一个景点的概率.21. 风筝起源于春秋战国时期,至今已有两千多年的历史.正值春日,周末小明姐弟俩在父母的陪同下来到一片宽广的场所放风筝.小明(A)与姐姐(B)一前一后在水平地面上放风筝,结果风筝在空中C处纠缠在一起,如图所示,测得 , 且小明与姐姐之间的距离 , 求此时风筝C处距离地面的高度.(参考数据: , 结果保留一位小数)
(1)、在图中作出关于x轴对称的;(2)、在(1)的条件下,分别写出点A、C的对应点、的坐标.20. 热情的刘老师邀请两位朋友茗茗和欣欣来西安游玩,他向两人推荐了四个游览地:兵马俑、西安城墙、华清宫和陕西省历史博物馆,并制作了四个外形完全一致的纸签,纸签上分别写有这四个游览地,让两位朋友随机抽取.抽签规则为:茗茗先抽签,放回洗匀后,再由欣欣抽签,(1)、茗茗抽取到“兵马俑”的概率为;(2)、请用树状图或列表法求两人抽取到同一个景点的概率.21. 风筝起源于春秋战国时期,至今已有两千多年的历史.正值春日,周末小明姐弟俩在父母的陪同下来到一片宽广的场所放风筝.小明(A)与姐姐(B)一前一后在水平地面上放风筝,结果风筝在空中C处纠缠在一起,如图所示,测得 , 且小明与姐姐之间的距离 , 求此时风筝C处距离地面的高度.(参考数据: , 结果保留一位小数)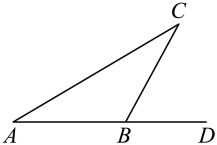 22. 某苹果种植户现有22吨苹果需要销售,经市场调查,采用批发、零售两种销售方式,这两种销售方式每天的销量及每顿所获得利润如表:
22. 某苹果种植户现有22吨苹果需要销售,经市场调查,采用批发、零售两种销售方式,这两种销售方式每天的销量及每顿所获得利润如表:销售方式
批发
零售
销量(吨/天)
5
2
利润(元/吨)
1200
2000
假设该种植户售完22吨苹果,共批发了x吨,所获总利润为y元,
(1)、求出x与y之间的函数关系式;(2)、因人手不够,该种植户每天只能采用一种销售方式销售,且正好5天销售完所有的苹果,计算该种植户所获总利润是多少元?23. 2023年大年初一上映两部电影,其一《满江红》以岳飞抗金为背景,讲述了南宋绍兴年间的历史事件,其二《流浪地球2》为观众展现末日危机下,人类在求生之路过程中的矛盾与冲突、勇气与团结.为了解学生对这两部影片的评价,某调查小组从该校九年级中随机抽取了20名学生对这两部作品分别进行打分(满分10分),并进行整理、描述和分析,下面给出了部分信息.《满江红》得分情况:7,8,7,10,7,6,9,9,10,10,8,9,8,6,6,10,9,7,9,9.抽取的学生对两部作品分别打分的平均数,众数和中位数:
平均数
众数
中位数
《满江红》
8.2
9
b
《流浪地球2》
7.8
c
8

根据以上信息,解答下列问题:
(1)、直接写出上述图表中的a,b,c的值;(2)、根据上述数据,你认为该校九年级学生对哪部作品评价更高?请说明理由(写出一条理由即可);(3)、若该校九年级1100名学生都对这两部作品进行打分,你认为这两部作品一共可得到多少个满分?24. 如图,在中,点E是的中点,连接 , 以为直径作 , 交于点D,为的切线. (1)、求证:;(2)、若 , , 求的长.
(1)、求证:;(2)、若 , , 求的长.

