广西壮族自治区梧州市苍梧县2023年中考一模数学试题
试卷更新日期:2023-05-18 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、20232. 2022年油价多次上涨,新能源车企迎来了更多的关注,如图是四款新能源汽车的标志,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知某细菌直径长约0.0000152米,那么该细菌的直径长用科学记数法可表示为( )A、152×105米 B、1.52×10﹣5米 C、﹣1.52×105米 D、1.52×10﹣4米4. 有理数在数轴上的对应点如图所示,这四个数中绝对值最小的是( )
3. 已知某细菌直径长约0.0000152米,那么该细菌的直径长用科学记数法可表示为( )A、152×105米 B、1.52×10﹣5米 C、﹣1.52×105米 D、1.52×10﹣4米4. 有理数在数轴上的对应点如图所示,这四个数中绝对值最小的是( ) A、a B、b C、c D、d5. 关于x的一元一次不等式3x≤4+x的解集在数轴上表示为( )A、
A、a B、b C、c D、d5. 关于x的一元一次不等式3x≤4+x的解集在数轴上表示为( )A、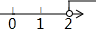 B、
B、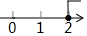 C、
C、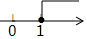 D、
D、 6. 下列运算,其中正确的是( )A、 B、 C、 D、7. 如图,该几何体的主视图是( )
6. 下列运算,其中正确的是( )A、 B、 C、 D、7. 如图,该几何体的主视图是( )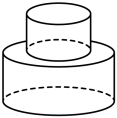 A、
A、 B、
B、 C、
C、 D、
D、 8. 已知x、y是二元一次方程组的解,那么的值是( )A、 B、 C、 D、9. 如图,直线 , 将三角尺的直角顶点放在直线b上,如果 , 那么的度数为( )
8. 已知x、y是二元一次方程组的解,那么的值是( )A、 B、 C、 D、9. 如图,直线 , 将三角尺的直角顶点放在直线b上,如果 , 那么的度数为( ) A、 B、 C、 D、10. 下列命题:①直线外一点到这条直线的垂线段,叫做点到直线的距离;②两点之间线段最短;③相等的圆心角所对的弧相等;④平分弦的直径垂直于弦.其中,真命题的个数是( )A、1 B、2 C、3 D、411. 已知圆锥的底面圆周长是 , 母线长是5,则这个圆锥的侧面积是( )A、 B、 C、 D、12. 如图,在正方形中,将边绕点B逆时针旋转至 , 连接 , , 若 , , 则线段的长度为( )
A、 B、 C、 D、10. 下列命题:①直线外一点到这条直线的垂线段,叫做点到直线的距离;②两点之间线段最短;③相等的圆心角所对的弧相等;④平分弦的直径垂直于弦.其中,真命题的个数是( )A、1 B、2 C、3 D、411. 已知圆锥的底面圆周长是 , 母线长是5,则这个圆锥的侧面积是( )A、 B、 C、 D、12. 如图,在正方形中,将边绕点B逆时针旋转至 , 连接 , , 若 , , 则线段的长度为( )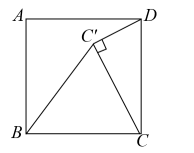 A、 B、 C、 D、3
A、 B、 C、 D、3二、填空题
-
13. 如果代数式有意义,那么x的取值范围是 .14. 分解因式: = .15. 如图,点A,B,C在上, , 则的度数为 .
 16. 我国北方有一个习俗:过年包饺子时会随机在饺子中包上糖果或硬币,我们称其为“幸运饺子”.吃到“幸运饺子”的人新的一年的日子会甜甜美美、万事如意.小亮家在大年初一时共煮了50个饺子,其中有4个“幸运饺子”,小亮从中随机挑选了一个饺子正好是“幸运饺子”的概率是 .17. 如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为 .
16. 我国北方有一个习俗:过年包饺子时会随机在饺子中包上糖果或硬币,我们称其为“幸运饺子”.吃到“幸运饺子”的人新的一年的日子会甜甜美美、万事如意.小亮家在大年初一时共煮了50个饺子,其中有4个“幸运饺子”,小亮从中随机挑选了一个饺子正好是“幸运饺子”的概率是 .17. 如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为 . 18. 如图,是等边三角形,边在轴上,反比例函数的图象经过点 , 若 , 点的坐标为 , 则k的值为.
18. 如图,是等边三角形,边在轴上,反比例函数的图象经过点 , 若 , 点的坐标为 , 则k的值为.
三、解答题
-
19. 计算:20. 化简:21. 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).

( 1 )画出△ABC关于y轴对称的;
( 2 )画出△ABC关于原点O成中心对称的 .
22. 已知:如图,在平行四边形中,点E、F在对角线上,且 , , (1)、求证:;(2)、求证:四边形是平行四边形.23. 2022年5月10日,搭载天舟四号货运飞船的长征七号遥五运载火箭,在我国文昌航天发射场点火发射,发射取得圆满成功.为激发广大青少年了解航天知识的热情,某校组织了航天知识的相关讲座和课程,并进行了航天知识竞赛,教务处随机抽取了50份竞赛卷进行统计,发现最低分为65分,最高分为100分,并绘制了如下尚不完整的统计图表.
(1)、求证:;(2)、求证:四边形是平行四边形.23. 2022年5月10日,搭载天舟四号货运飞船的长征七号遥五运载火箭,在我国文昌航天发射场点火发射,发射取得圆满成功.为激发广大青少年了解航天知识的热情,某校组织了航天知识的相关讲座和课程,并进行了航天知识竞赛,教务处随机抽取了50份竞赛卷进行统计,发现最低分为65分,最高分为100分,并绘制了如下尚不完整的统计图表.组别
成绩x(分)
频数(人数)
各组总分(分)
A
95≤x≤100
8
778
B
85≤x<95
m
2070
C
75≤x<85
n
1280
D
65≤x<75
3
222

请根据图表提供的信息,解答下列问题:
(1)、m= , C组所占圆心角度数为°;(2)、此次被抽取的竞赛卷成绩的中位数落在 组,并求此次被抽取的竞赛卷成绩的平均数;(3)、学校计划对成绩为95≤x≤100的学生进行奖励,若该校共有1000人参加此次竞赛,请估计此次竞赛获得奖励的学生人数.24. 甲、乙两支工程队修建二级公路,已知甲队每天修路的长度是乙队的2倍,如果两队各自修建公路500m , 甲队比乙队少用5天.(1)、求甲,乙两支工程队每天各修路多少米?(2)、我市计划修建长度为3600 m的二级公路,因工程需要,须由甲、乙两支工程队来完成.若甲队每天所需费用为1.2万元,乙队每天所需费用为0. 5万元,求在总费用不超过40万元的情况下,至少安排乙队施工多少天?