沪科版数学七年级下册10.1相交线 同步练习
试卷更新日期:2023-05-18 类型:同步测试
一、单选题(每题3分,共30分)
-
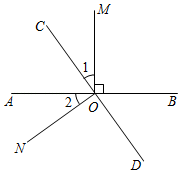
1. 如图各图中,∠1与∠2是对顶角的是( )A、
 B、
B、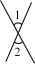 C、
C、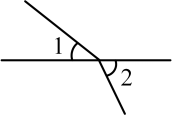 D、
D、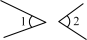 2. 如图,直线a,b被直线c所截,下列说法中不正确的是( )
2. 如图,直线a,b被直线c所截,下列说法中不正确的是( )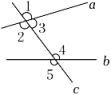 A、∠1与∠2是对顶角 B、∠2与∠5是同位角 C、∠3与∠5是同旁内角 D、∠2与∠4是内错角3. 下列说法中,正确的是( )A、两点之间直线最短 B、如果∠α=53°38',那么∠α余角的度数为36.22° C、如果一个角的余角和补角都存在,那么这个角的余角比这个角的补角小 D、相等的角是对顶角4. 如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
A、∠1与∠2是对顶角 B、∠2与∠5是同位角 C、∠3与∠5是同旁内角 D、∠2与∠4是内错角3. 下列说法中,正确的是( )A、两点之间直线最短 B、如果∠α=53°38',那么∠α余角的度数为36.22° C、如果一个角的余角和补角都存在,那么这个角的余角比这个角的补角小 D、相等的角是对顶角4. 如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( ) A、垂线段最短 B、两点确定一条直线 C、两点之间,线段最短 D、过直线外一点有且只有一条直线与已知直线平行5. 在同一平面内,下列命题是假命题的是( )A、过直线外一点有且只有一条直线与已知直线相交 B、已知 , , 三条直线,若 , , 则 C、在同一平面内,过直线外一点有且只有一条直线与已知直线垂直 D、若三条直线两两相交,则它们有一个或三个交点6. 如图,直线交于点O, , 把分为两部分,且 , 则的度数为( )
A、垂线段最短 B、两点确定一条直线 C、两点之间,线段最短 D、过直线外一点有且只有一条直线与已知直线平行5. 在同一平面内,下列命题是假命题的是( )A、过直线外一点有且只有一条直线与已知直线相交 B、已知 , , 三条直线,若 , , 则 C、在同一平面内,过直线外一点有且只有一条直线与已知直线垂直 D、若三条直线两两相交,则它们有一个或三个交点6. 如图,直线交于点O, , 把分为两部分,且 , 则的度数为( ) A、120° B、140° C、108° D、126°7. 如图,直线a、b被c所截,下列说法中错误的是( )
A、120° B、140° C、108° D、126°7. 如图,直线a、b被c所截,下列说法中错误的是( ) A、∠1的对顶角是47° B、∠1的内错角是47° C、∠1的同旁内角是133° D、∠1的同位角是47°8. 如图,点C到直线的距离是( )
A、∠1的对顶角是47° B、∠1的内错角是47° C、∠1的同旁内角是133° D、∠1的同位角是47°8. 如图,点C到直线的距离是( ) A、线段的长度 B、线段的长度 C、线段的长度 D、线段的长度9. 下列说法正确的个数( )
A、线段的长度 B、线段的长度 C、线段的长度 D、线段的长度9. 下列说法正确的个数( )①过一点有且只有一条直线与已知直线垂直;②平面内,互相垂直的两条直线一定相交;③有公共顶点且相等的角是对顶角;④直线外一点到已知直线的垂线段,叫做这点到直线的距离;⑤过一点有且只有一条直线与已知直线平行.
A、0个 B、1个 C、2个 D、3个10. 将一副直角三角板如图放置,使两直角边重合,则的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空2分,共12分)
-
11. 已知:如图,直线BO⊥AO于点O,OB平分∠COD,∠BOD=22°.则∠AOC的度数是 度.
 12. 如图,直线、被直线所截,交点分别为M、N,则的同位角是.
12. 如图,直线、被直线所截,交点分别为M、N,则的同位角是.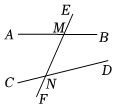 13. 下列三个日常现象:
13. 下列三个日常现象:
其中,可以用“垂线段最短”来解释的是 (填序号).
14. 如图,AB与BC被AD所截得的内错角是;DE与AC被直线AD所截得的内错角是;图中∠4的内错角是 . 15. 观察下列各图,寻找对顶角(不含平角).如图1,图中有2条直线相交,则对顶角有对;如图2,图中有3条直线相交于一点,则对顶角有对;如图3图中有条直线相交于一点,则对顶角有对.
15. 观察下列各图,寻找对顶角(不含平角).如图1,图中有2条直线相交,则对顶角有对;如图2,图中有3条直线相交于一点,则对顶角有对;如图3图中有条直线相交于一点,则对顶角有对.
三、作图题(共10分)
-
16. 根据下列要求画图,(1)、如图(1)所示,过点A画;
 (2)、如图(2)所示,过点P画 , 垂足为E,过点P画 , 垂足为G.
(2)、如图(2)所示,过点P画 , 垂足为E,过点P画 , 垂足为G.
四、解答题(共5题,共48分)
-
17. 如图,直线相交于点O, , 平分 , .
 (1)、当时,求的度数(填空完成下列说理过程);
(1)、当时,求的度数(填空完成下列说理过程);解: (已知)
_▲_
_▲_(邻补角定义)
_▲_
平分(已知)
_▲_ ( )
_▲_
(2)、当时,(直接填空).18. 两条直线被第三条直线所截.∠1是∠2的同旁内.角,∠2是∠3的内错角.(1)、画出示意图,标出∠1,∠2,∠3;(2)、若∠1=2∠2,∠2=2∠3,求∠3的度数.19. 对于复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零,这是一种常见的数学解题思想. (1)、如图1.直线l1、l2被直线l3所截,在这个基本图形中,形成了对同旁内角.(2)、如图2.平面内三条直线l1 , l2 , l3两两相交,交点分别为A,B,C,图中一共有对同旁内角.(3)、平面内四条直线两两相交,最多可以形成对同旁内角
(1)、如图1.直线l1、l2被直线l3所截,在这个基本图形中,形成了对同旁内角.(2)、如图2.平面内三条直线l1 , l2 , l3两两相交,交点分别为A,B,C,图中一共有对同旁内角.(3)、平面内四条直线两两相交,最多可以形成对同旁内角
-