2022~2023学年浙教版数学七年级下学期期末模考数学试卷（三）

试卷更新日期：2023-05-18 类型：期末考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. （﹣xy³）²=（　　）

A、x²y⁵ B、﹣x²y⁵ C、xy⁶ D、x²y⁶

查看试题解析
2. 下面的每组图形中，左面的平移后可以得到右面的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，直线 AD，BE 被直线 BF 和 AC所截，则∠1的同位角和∠5的内错角分别是（）

A、∠4，∠2 B、∠2，∠6 C、∠5，∠4 D、∠2，∠4

查看试题解析
4. 下列因式分解正确的是（　　）

A、a²﹣b²=（a﹣b）² B、x²+4y²=（x+2y）² C、2﹣8a²=2（1+2a）（1﹣2a） D、x²﹣4y²=（x+4y）（x﹣4y）

查看试题解析
5. 用加减消元法解二元一次方程组 ${\begin{cases} x + 3 y = 4 ① \\ 2 x - y = 1 ② \end{cases}$ 时，下列方法中无法消元的是（）

A、①×2-② B、②×3+① C、①-②×3 D、①×（-2）+②

查看试题解析
6. 若方程组 $\{\begin{matrix} 2 x + y = m \\ x + y = 3 \end{matrix}$ 的解是 $\{\begin{matrix} x = 2 \\ y = n \end{matrix}$ 则m、n表示的数分别是（）

A、5，1 B、1，4 C、2，3 D、2，4

查看试题解析
7.
某校九（3）班的全体同学喜欢的球类运动用如图所示的统计图来表示，下面说法正确的是（　　）

A、从图中可以直接看出喜欢各种球类的具体人数 B、从图中可以直接看出全班的总人数 C、从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况 D、从图中可以直接看出全班同学现在喜欢各种球类人数的大小关系

查看试题解析
8.
如图，△ABC沿着由点B到点E的方向，平移到△DEF，已知BC=5．EC=3，那么平移的距离为（　　）

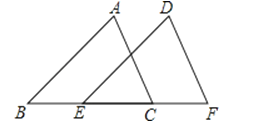A、2 B、3 C、5 D、7

查看试题解析
9. 已知实数x，y，z满足 ${\begin{array}{l} x + y + z = 7 \\ 4 x + y - 2 z = 2 \end{array}$ ，则代数式3(x﹣z)+1的值是（）

A、﹣2 B、﹣4 C、﹣5 D、﹣6

查看试题解析
10. 如图是由10个相同的小长方形木板无缝隙的拼成的一个大长方形木板，设小长方形的长为xcm，宽为ycm，根据题意可列方程组为（）

A、 ${\begin{cases} x + 2 y = 15 \\ 3 x = y \end{cases}$ B、 ${\begin{cases} 2 x + y = 15 \\ x = 3 y \end{cases}$ C、 ${\begin{cases} 2 x+ y = 15 \\ x = 3 y \end{cases}$ D、 ${\begin{cases} x + 2y = 15 \\ x = 3 y \end{cases}$

查看试题解析

二、填空题（共6题，每题4分，共24分）

11. 分解因式：x²﹣64=.

查看试题解析
12. 若 $\frac{1}{x} + \frac{1}{y} = 2$ ，则 $\frac{2 x + x y + 2 y}{3 x + 5 x y + 3 y} =$ ．

查看试题解析
13. 要在规定的日期内加工一批机器件,如果甲单独做,刚好在规定日期内完成,乙单独做则要超过3天.现在甲乙两人合作2天后,再由乙单独做,正好按期完成.则规定日期是天

查看试题解析
14. 为表彰“我爱读书”演讲比赛中获奖同学，老师决定购买笔记本与钢笔作为奖品，已知5个笔记本和2支钢笔共需100元：4个笔记本和7支钢笔共需161元．设每个笔记本z元，每支钢笔y元，根据题意可列方程组为

查看试题解析
15. 若（x²+px+8）•（x²﹣3x+1）的结果中不含x³项，则P=

查看试题解析
16.
为了了解2014年某地区10万名大、中、小学生50米跑成绩情况，教育部门从这三类学生群体中各抽取了10%的学生进行检测，整理样本数据，并结合2010年抽样结果，得到下列统计图：

（1）本次检测抽取了大、中、小学生共名，其中小学生名；
（2）根据抽样的结果，估计2014年该地区10万名大、中、小学生中，50米跑成绩合格的中学生人数为名．

查看试题解析

三、解答题（共8题，共46分）

17. 综合题。

(1)、（1﹣π）× $\sqrt[3]{27}$ ﹣（ $\frac{1}{7}$ ）^﹣¹+|﹣2|

(2)、先化简，再求值： $\frac{a^{2} - 2 a}{a^{2} - 1}$ ÷（a﹣1﹣ $\frac{2 a - 1}{a + 1}$ ，其中a=3．

查看试题解析
18. 解下列方程组：

(1)、 ${\begin{array}{l} 2 x - 5 y = - 13 \\ x + 3 y = 10 \end{array}$

(2)、 ${\begin{array}{l} \frac{x}{4} + \frac{y}{3} = 3 \\ 3 x - 2 (y - 1) = 11 \end{array}$

查看试题解析
19. 如图，已知点A、D、B在同一直线上，∠1＝∠2，∠BCD＝∠E，试判断DE、BC有怎样的位置关系，并说明理由．

查看试题解析
20. 已知关于x、y的方程组 ${\begin{array}{l} 2 x - 3 y = 3 \\ a x + b y = - 1 \end{array}$ 的解和 ${\begin{array}{l} 2 a x + 3 b y = 3 \\ 3 x + 2 y = 11 \end{array}$ 的解相同，求代数式 $b - a$ 的平方根.

查看试题解析
21. 购买一批布料给校文艺队每人做一套演出服，大号每套需要布料4.9米，中号每套需要布料4.2米．若全部做大号，则差布3.9米，若全部做中号，则余布3.8米，请你算一算，校文艺队有几名队员，共购买了多少米布?

查看试题解析
22.
如图，将一个长小形铁皮剪去一个小正方形．
（1）用含有a，b的代数式表示余下阴影部分的面积；
（2）当a=6，b=2时，求余下阴影部分的面积．

查看试题解析
23.
某校为了解九年级学生近两个月“推荐书目”的阅读情况，随机抽取了该年级的部分学生，调查了他们每人“推荐书目”的阅读本数．设每名学生的阅读本数为n，并按以下规定分为四档：当n＜3时，为“偏少”；当3≤n＜5时，为“一般”；当5≤n＜8时，为“良好”；当n≥8时，为“优秀”．将调查结果统计后绘制成不完整的统计图表：
阅读本数n（本）
1
2
3
4
5
6
7
8
9
人数（名）
1
2
6
7
12
x
7
y
1
请根据以上信息回答下列问题：
（1）求出本次随机抽取的学生总人数；
（2）分别求出统计表中的x，y的值；
（3）估计该校九年级400名学生中为“优秀”档次的人数．

查看试题解析
24. 先阅读，再回答问题：要比较代数式A、B的大小，可以作差A﹣B，比较差的取值，当A﹣B＞0时，有A＞B；当A﹣B=0时，有A=B；当A﹣B＜0时，有A＜B．”例如，当a＜0时，比较a²和a（a+1）的大小．可以观察a²﹣a（a+1）=a²﹣a²﹣a=﹣a．因为当a＜0时，﹣a＞0，所以当a＜0时，a²＞a（a+1）．

(1)、已知M=（x﹣2）（x﹣16），N=（x﹣4）（x﹣8），比较M、N的大小关系．

(2)、某种产品的原料提价，因而厂家决定对于产品进行提价，现有三种方案：
方案1：第一次提价p%，第二次提价q%；
方案2：第一次提价q%，第二次提价p%；
方案3：第一、二次提价均为 $\frac{p + q}{2}$ %．
如果设原价为a元，请用含a、p、q的式子表示提价后三种方案的价格．
方案1：；方案2：；方案3：
如果p，q是不相等的正数，三种方案哪种提价最多？

查看试题解析

阅读本数n（本）	1	2	3	4	5	6	7	8	9
人数（名）	1	2	6	7	12	x	7	y	1