2022~2023学年浙教版数学七年级下学期期末模考数学试卷(二)
试卷更新日期:2023-05-18 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 如图,下列说法中不正确的是( )
 A、和是同旁内角 B、和是内错角 C、和是同位角 D、和是对顶角2. 每年的5月8日是世界微笑日,在对别人的微笑中,你也会看到世界对自己微笑起来.下列图案是由图中所示的图案平移得到的是( )
A、和是同旁内角 B、和是内错角 C、和是同位角 D、和是对顶角2. 每年的5月8日是世界微笑日,在对别人的微笑中,你也会看到世界对自己微笑起来.下列图案是由图中所示的图案平移得到的是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 下列各式中能用完全平方公式因式分解的是( )A、 B、 C、 D、5. 太原某公司对某款新产品的生产成本进行调查,并绘制了如下扇形统计图,则材料费所在扇形的圆心角的度数是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 下列各式中能用完全平方公式因式分解的是( )A、 B、 C、 D、5. 太原某公司对某款新产品的生产成本进行调查,并绘制了如下扇形统计图,则材料费所在扇形的圆心角的度数是( ) A、 B、 C、 D、6. 已知是二元一次方程组的解,则 , 的值分别是( )A、 B、 C、 D、7. 将一块三角板沿一条直角边所在的直线向右平移个单位到位置,如图所示.下列结论:①且;②且;③;④若 , , 则边边扫过的图形的面积为5,正确的个数有( )
A、 B、 C、 D、6. 已知是二元一次方程组的解,则 , 的值分别是( )A、 B、 C、 D、7. 将一块三角板沿一条直角边所在的直线向右平移个单位到位置,如图所示.下列结论:①且;②且;③;④若 , , 则边边扫过的图形的面积为5,正确的个数有( ) A、4 B、3 C、2 D、18. 已知为正整数,且二元一次方程组有整数解,则的值为( )A、 B、 C、 D、9. 已知实数x,y,z满足 , 则代数式3(x﹣z)+1的值是( )A、﹣2 B、﹣4 C、﹣5 D、﹣610. 孙子算经是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长,绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为尺,绳子长为尺,则所列方程组正确的是
A、4 B、3 C、2 D、18. 已知为正整数,且二元一次方程组有整数解,则的值为( )A、 B、 C、 D、9. 已知实数x,y,z满足 , 则代数式3(x﹣z)+1的值是( )A、﹣2 B、﹣4 C、﹣5 D、﹣610. 孙子算经是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长,绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为尺,绳子长为尺,则所列方程组正确的是 ( ) A、 B、 C、 D、
( ) A、 B、 C、 D、二、填空题(每空4分,共24分)
-
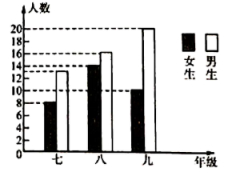
11. 分解因式:a2-4=12. 计算: .13. 如图,所提供的信息错误的是(填序号).
①七年级学生总数最多
②九年级的男生数是女生数的两倍
③女生总数比男生总数少16人
④八年级的学生总数比九年级的学生总数多
 14. 若(x-1)(x2+ax+2)的展开式中不含x2项,则a的值是15. 某感冒药用来计算儿童服药量的公式为 , 其中为成人服药量,为儿童的年龄 , 如果一个儿童的服药量恰好是成人服药量的 , 那么他的年龄是 岁16. 《九章算术》是我国东汉初年编订的一部数学经典著作,其中一伙力桎组是用算筹布置而成,如图(1)所示的算筹图用我们现在所熟悉的方程组表示出来,就是 , 类似的,图(2)所示的算筹图用方程组表示出来,就是
14. 若(x-1)(x2+ax+2)的展开式中不含x2项,则a的值是15. 某感冒药用来计算儿童服药量的公式为 , 其中为成人服药量,为儿童的年龄 , 如果一个儿童的服药量恰好是成人服药量的 , 那么他的年龄是 岁16. 《九章算术》是我国东汉初年编订的一部数学经典著作,其中一伙力桎组是用算筹布置而成,如图(1)所示的算筹图用我们现在所熟悉的方程组表示出来,就是 , 类似的,图(2)所示的算筹图用方程组表示出来,就是
三、解答题(共8题,共46分)
-
17. 解方程组(1)、(2)、18. 先化简,后求值: , 其中的值从 , , , 中选一个合适的数.19. 完成下面推理过程:
如图,点G,D,F共线,且 , , 求证:.
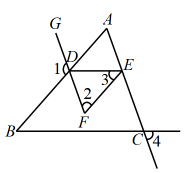
证明:∵ , (已知),
∴( ),
∴( ).
∴( ).
∵ ,
∴( ).
∴( ).
∴( ).
∵( ).
∴( ).
20. 若方程组和方程组有相同的解,求a,b的值.21. 2022年冬奥会上智慧化全覆盖,机器人得到广泛应用,冬奥会组委会针对不同的物品运送场景选取了几个不同类型的智能物流机器人.这样不仅能高效运输,同时也能减少人员接触.具体运输情况如下表所示:A型机器人/个
B型机器人/个
运输物品总数/件
第一批
2
5
34
第二批
4
3
26
问:每个型机器人和型机器人分别可以运输物品多少件?
22. 小丽、小宁和小明同时计算 , 下面是他们三人的一段对话:小丽:我的答案中常数项是;小宁:我的答案中没有一次项;小明:你们说得都正确,我还知道;请你根据他们的对话确定a、b的值.23. 为了解居民对垃圾分类相关知识的知晓程度(“A.非常了解”,“B.了解”,“C.基本了解”,“D.不太了解”),小明随机调查了若干人(每人必选且只能选择四种程度中的一种).根据调查结果绘制成如图两幅不完整的统计图,请你把两幅统计图补充完整,并估计50000名市民中不太了解垃圾分类相关知识的人数.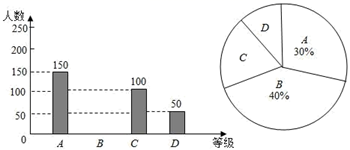 24. [学习材料]拆项添项法
24. [学习材料]拆项添项法在对某些多项式进行因式分解时,需要把多项式中的某一项拆成两项或多项,或者在多项式中添上两个仅符号相反的项,这样的分解因式的方法称为拆项添项法。如:
例1、分解因式:x4+4y4
解:原式=x4+4y4=x4+4x2y2+4y4-4x2y2
=(x2+2y2)2-4x2y2=(x2+2y2+2xy)(x2+2y2-2xy)
例2、分解因式:x3+5x-6
解:原式=x3-x+6x-6=x(x2-1)+6(x-1)=(x-1)(x2+x+6)
我们还可以通过拆项对多项式进行变形,如
例3、把多项式a2+b2+4a-6b+13写成A2+B2的形式.
解:原式=a2+4a+4+b2-6b+9=(a+2)2+(b-3)2
[知识应用]请根据以上材料中的方法,解决下列问题:
(1)、分解因式:x2+2x-8=(2)、分解因式:x4+4=(3)、关于x的二次三项式x2-20x+111在x=时,有最小值;(4)、已知M=x2+6x+4y2-12y+m(x-y均为整数,m是常数),若M恰能表示成A2+B2的形式,求m的值.