2022~2023学年浙教版数学八年级下学期期末模考数学试卷(五)
试卷更新日期:2023-05-18 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 方程x(2x+1)=5(2x+1)的根是( )A、5和 B、 C、5 D、-5和2. 某超市购进一批商品,单价40元.经市场调查,销售定价为52元时,可售出180个,定价每增加1元,销售量减少10个,因受库存的影响,每批次进货个数不得超过180个,超市若将准备获利2000元,则定价为多少元?( )A、50 B、60 C、50或60 D、1003. 小杭同学将自己前7次体育模拟测试成绩(单位一分)统计如表,第8次测试的成绩为a分,若这8次成绩的众数不止一个,则a的值为( )
次数
第1次
第2次
第3次
第4次
第5次
第6次
第7次
成绩
27
28
30
28
29
29
28
A、27 B、28 C、29 D、304. 如图,点是内一点,点是边的中点,交边于点 , . 若 , 则的长为( )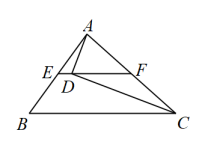 A、0.5 B、1 C、1.5 D、25. 已知三角形的三边长分别为a、b、c,求其面积问题,中外数学家曾经进行过深入研究,古希腊的几何学家海伦(Heron,约公元50年)给出求其面积的海伦公式S= , 其中p=;我国南宋时期数学家秦九韶(约1202-1261)曾提出利用三角形的三边求其面积的秦九韶公式S= , 若一个三角形的三边长分别为2,3,4,则其面积是( )A、 B、 C、 D、6. 如图1,将一张长20cm,宽10cm的长方形硬纸片裁剪掉图中阴影部分之后,恰好折成如图2的有盖长方体纸盒,纸盒底面积为 , 则该有盖纸盒的高为( )
A、0.5 B、1 C、1.5 D、25. 已知三角形的三边长分别为a、b、c,求其面积问题,中外数学家曾经进行过深入研究,古希腊的几何学家海伦(Heron,约公元50年)给出求其面积的海伦公式S= , 其中p=;我国南宋时期数学家秦九韶(约1202-1261)曾提出利用三角形的三边求其面积的秦九韶公式S= , 若一个三角形的三边长分别为2,3,4,则其面积是( )A、 B、 C、 D、6. 如图1,将一张长20cm,宽10cm的长方形硬纸片裁剪掉图中阴影部分之后,恰好折成如图2的有盖长方体纸盒,纸盒底面积为 , 则该有盖纸盒的高为( )
 A、4cm B、3cm C、2cm D、1cm7. 如图,是正方形边上一点,将绕点顺时针旋转得 , 连接 , 过点作的垂线交于点 , 交于点.若 , , 则的长为( )
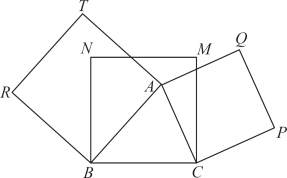
A、4cm B、3cm C、2cm D、1cm7. 如图,是正方形边上一点,将绕点顺时针旋转得 , 连接 , 过点作的垂线交于点 , 交于点.若 , , 则的长为( ) A、 B、 C、4 D、8. 如图,菱形的对角线长度为4,边长 , M为菱形外一个动点,满足 , N为中点,连接.则当M运动的过程中,长度的最大值为( )
A、 B、 C、4 D、8. 如图,菱形的对角线长度为4,边长 , M为菱形外一个动点,满足 , N为中点,连接.则当M运动的过程中,长度的最大值为( ) A、 B、 C、1 D、29. 某市举行中学生数学知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,.其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次数学知识竞赛中成绩优秀人数最多的是( ).
A、 B、 C、1 D、29. 某市举行中学生数学知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,.其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次数学知识竞赛中成绩优秀人数最多的是( ).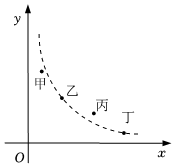 A、甲 B、乙 C、丙 D、丁10. 如图,在平面直角坐标系中, , , , , 把一条长为2023个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点处,并按…的规律绕在四边形的边上,则细线另一端所在位置的点的坐标是( )
A、甲 B、乙 C、丙 D、丁10. 如图,在平面直角坐标系中, , , , , 把一条长为2023个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点处,并按…的规律绕在四边形的边上,则细线另一端所在位置的点的坐标是( )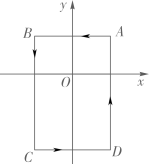 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空4分,共24分)
-
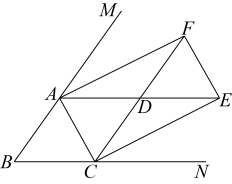
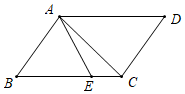
11. 计算的结果是 .12. 一组数据:3,9,2, , 7,它的中位数是4,则这组数据的平均数是 .13. 目前以等为代表的战略性新兴产业蓬勃发展.某市2021年底有用户2万户,计划到2023年底全市用户数累计达到8.72万户.设全市用户数年平均增长率为 , 则根据题意可列方程为 .14. 如图,在▱中,平分交于点 , 连接若 , , 则的度数为.
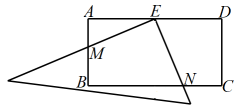
 15. 如图,点是正方形中延长线上一点,连接 , 点是的中点,连接 , 若 , , 则的长为 .
15. 如图,点是正方形中延长线上一点,连接 , 点是的中点,连接 , 若 , , 则的长为 .
 16. 如图,在平面直角坐标系中,矩形的边落在y轴上,其它部分均在第一象限,双曲线过点A,延长对角线交x轴于点E,以为邻边作平行四边形 , 若平行四边形的面积为7,则k为 .
16. 如图,在平面直角坐标系中,矩形的边落在y轴上,其它部分均在第一象限,双曲线过点A,延长对角线交x轴于点E,以为邻边作平行四边形 , 若平行四边形的面积为7,则k为 .
三、解答题(共8题,共46分)
-
17. 已知:a= , b= , 求a2-ab+b2的值.18. 某商店以每个8元的成本价购进了一批玩具陀螺,如果以每个14元的价格出售,那么每天可销售40个,经市场调查发现,若每个陀螺的售价每上涨1元,则每天的销售量就减少2个.每个陀螺涨价多少元时,才能让顾客得到实惠的同时商店每天获得的利润为320元?19. 甲、乙两名射击运动员各进行10次射击,甲的成绩是7,7,8,9,8,9,10,9,9,9.乙的成绩如图所示(单位:环)
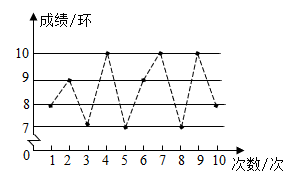 (1)、分别计算甲、乙两人射击成绩的平均数;(2)、若要选拔一人参加比赛,应派哪一位?请说明理由.20. 以下是小滨在解方程时的解答过程.
(1)、分别计算甲、乙两人射击成绩的平均数;(2)、若要选拔一人参加比赛,应派哪一位?请说明理由.20. 以下是小滨在解方程时的解答过程.解:原方程可化为
解得原方程的解是.
小滨的解答是否有错误?如果有错误,请写出正确的解答过程.
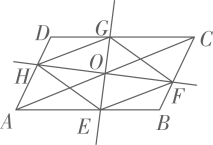
21. 如图,过的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H四点,连接EF,FG,GH,HE.试判断四边形EFGH的形状,并说明理由.