2022~2023学年浙教版数学八年级下学期期末模考数学试卷(二)
试卷更新日期:2023-05-18 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 下列各式中,属于二次根式的是( )A、 B、 C、 D、2. 某小组同学在一周内参加家务劳动的时间统计如下表,下列说法正确的是( )
劳动时间/h
3
3.5
4
4.5
人数
1
1
2
1
A、中位数是3.75,众数是4 B、中位数是3.5,众数是4 C、中位数是4,众数是4 D、中位数是4,众数是23. 已知m是一元二次方程的一个根,则的值为( )A、 B、 C、6 D、4. 在中,已知 , 则的度数为( )A、 B、 C、 D、5. 下列说法正确的是( )A、两组对角分别相等的四边形是平行叫边形 B、两条对角线互相垂直的四边形是菱形 C、两条对角线相等的四边形是矩形 D、两条对角线垂直且相等的四边形是正方形6. 面积为2的直角三角形的一条直角边长为x,另一条直角边长为y,则y与x的变化规律用图象大致表示为( )A、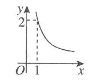 B、
B、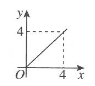 C、
C、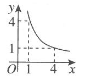 D、
D、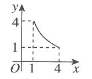 7. 为响应国家“双减政策”,某校2021年第三季度平均每周作业时长为600分钟,经过2021年第四季度和2022年第一季度两次整改后,平均每周作业时长为350分钟.设每季度平均每周作业时长的下降率为a,则可列方程为( )A、600(1-a)=350 B、350(1+a)=600 C、600(1-a)2=350 D、350(1+a)2=6008. 图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数的图象上, , , 则正方形ADEF的边长为( )
7. 为响应国家“双减政策”,某校2021年第三季度平均每周作业时长为600分钟,经过2021年第四季度和2022年第一季度两次整改后,平均每周作业时长为350分钟.设每季度平均每周作业时长的下降率为a,则可列方程为( )A、600(1-a)=350 B、350(1+a)=600 C、600(1-a)2=350 D、350(1+a)2=6008. 图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数的图象上, , , 则正方形ADEF的边长为( ) A、1 B、2 C、 D、39. 如图,在正方形ABCD中,已知边长 , 点E是BC边上一动点(点E不与B、C重合),连接AE,作点B关于直线AE的对称点F,则线段CF的最小值为( )
A、1 B、2 C、 D、39. 如图,在正方形ABCD中,已知边长 , 点E是BC边上一动点(点E不与B、C重合),连接AE,作点B关于直线AE的对称点F,则线段CF的最小值为( ) A、5 B、 C、 D、10. 如图,矩形ABCD为一个正在倒水的水杯的截面图,杯中水面与CD的交点为E,当水杯底面BC与水平面的夹角为27°时,∠AED的大小为( )
A、5 B、 C、 D、10. 如图,矩形ABCD为一个正在倒水的水杯的截面图,杯中水面与CD的交点为E,当水杯底面BC与水平面的夹角为27°时,∠AED的大小为( ) A、27° B、53° C、57° D、63°
A、27° B、53° C、57° D、63°二、填空题(每题4分,共24分)
-
11. 若多边形的每个内角都相等且内角和是540°,则该多边形的一个外角为 °.12. 将一元二次方程化成(a,b 为常数)的形式,则ab= .13. 已知一组数据1,5,2,4,x的平均数是3,则x=;这组数据的方差为 .14. 若关于x的一元二次方程x2-(m-2)x+4=0 有两个相等实数根,则m=.15. 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴负半轴上.反比例函数y=(x<0)的图象经过菱形对角线的交点A,若点D的坐标为(-3,4),则k等于 .
 16. 如图,正方形ABCD的边长为2,G是对角线BD上一动点,GE⊥CD于点E,GF⊥BC于点F,连结EF.给出四种情况:
16. 如图,正方形ABCD的边长为2,G是对角线BD上一动点,GE⊥CD于点E,GF⊥BC于点F,连结EF.给出四种情况:
①若G为BD上任意一点,则AG=EF;
②若BG=AB,则∠DAG=22.5°;
③若G为BD的中点,则四边形CEGF是正方形;
④若DG:BG=1:3,则S△ADG=
则其中正确的是.
三、解答题(共8题,共46分)
-
17. 解方程(1)、x2-4x+1=0(2)、(x-3)2-4x2=0.18. 先化简,再求值: , 其中 .19. 如图,在中, , 、分别是、的中点,试判断四边形的形状,并证明之.
 20. 2022年5月30日是第六个全国科技工作者日,主题为“创新争先,自立自强”.为了庆祝第六个全国科技工作者日,学校举办科技知识竞赛活动,竞赛内容分“航天技术”,“生物技术”,“能源技术”,“其它技术领域”四个项目,下表是小亮和小明的各项成绩:(百分制)
20. 2022年5月30日是第六个全国科技工作者日,主题为“创新争先,自立自强”.为了庆祝第六个全国科技工作者日,学校举办科技知识竞赛活动,竞赛内容分“航天技术”,“生物技术”,“能源技术”,“其它技术领域”四个项目,下表是小亮和小明的各项成绩:(百分制)航天技术
生物技术
能源技术
其它技术领域
小亮
85
90
95
90
小明
100
90
80
90
若“航天技术”,“生物技术”,“能源技术”,“其它技术领域”四个项目按确定综合成绩,则小亮和小明谁的综合成绩高?请通过计算说明理由.
21. 如图,某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为),另外三面用栅栏围成,已知栅栏总长度为 , 设矩形垂直于墙的一边,即的长为.若矩形养殖场的面积为 , 求此时的x的值.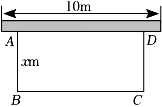 22. 在平面直角坐标系xOy中,过原点O的直线l1与双曲线 的一个交点为A(1,m).(1)、求直线l1的表达式;(2)、过动点P(n,0)(n>0)且垂直于x轴的直线与直线l1和双曲线 的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
22. 在平面直角坐标系xOy中,过原点O的直线l1与双曲线 的一个交点为A(1,m).(1)、求直线l1的表达式;(2)、过动点P(n,0)(n>0)且垂直于x轴的直线与直线l1和双曲线 的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.

