2022~2023学年浙教版数学八年级下学期期末模考数学试卷(一)
试卷更新日期:2023-05-18 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、-2. 下列方程是一元二次方程的是( )A、 B、2x-3=3(x+7) C、 D、3. 选择用反证法证明“已知:在中,求证: , 中至少有一个角不大于”时,应先假设( )A、 , B、 , C、 , D、 ,4. 某校开展了“好书伴我成长”读书活动,为了解4月份八年级学生的读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示,下列说法正确的是( )
册数
0
1
2
3
4
人数
4
12
16
17
1
A、方差是2 B、中位数是2 C、平均数是2 D、众数是175. 已知一次函数的图象如图所示,则与的图象在同一坐标系中正确的是( )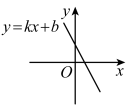 A、
A、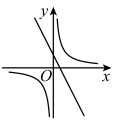 B、
B、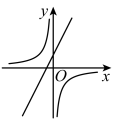 C、
C、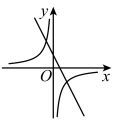 D、
D、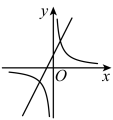 6. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则符合题意的方程是( )A、 B、 C、 D、7. 如图,▱的周长是 , 对角线与交于点 , , 是中点,的周长比的周长多 , 则的长为( )
6. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则符合题意的方程是( )A、 B、 C、 D、7. 如图,▱的周长是 , 对角线与交于点 , , 是中点,的周长比的周长多 , 则的长为( ) A、5 B、 C、4 D、8. 反比例函数 图象上有三个点 , 其中 , 则 的大小关系是( )A、 B、 C、 D、9. 勾股定理在平面几何中有着不可替代的重要地位,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载,图(a)是由边长均为1的小正方形和Rt△BAC构成,可以用其面积关系验证勾股定理,将图(a)按图(b)所示的方式“嵌入”长方形LMJK,则该长方形的面积为( ).
A、5 B、 C、4 D、8. 反比例函数 图象上有三个点 , 其中 , 则 的大小关系是( )A、 B、 C、 D、9. 勾股定理在平面几何中有着不可替代的重要地位,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载,图(a)是由边长均为1的小正方形和Rt△BAC构成,可以用其面积关系验证勾股定理,将图(a)按图(b)所示的方式“嵌入”长方形LMJK,则该长方形的面积为( ). A、60 B、100 C、110 D、12110. 用配方法解一元二次方程 , 配方后得到的方程是( )A、 B、 C、 D、
A、60 B、100 C、110 D、12110. 用配方法解一元二次方程 , 配方后得到的方程是( )A、 B、 C、 D、二、填空题(每空4分,共24分)
-
11. 若多边形的每个内角都相等且内角和是540°,则该多边形的一个外角为 °.12. 随着新冠疫情趋于缓和,口罩市场趋于饱和,某N95口罩每盒原价为200元,连续两次降价后每盒的售价为72元,则平均每次下降的百分率为 .13. 如图所示的是莉莉次购买某水果的重量(单位,)的统计图,则次重量的中位数是 .
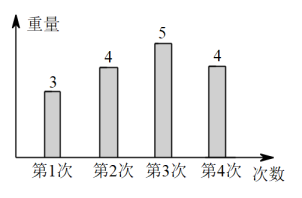 14. 已知m是一元二次方程的一个根,则的值是.15. 小颖将能够活动的菱形学具活动成为图1所示形状,并测得 , .接着,她又将这个学其活动成为图2所示正方形,此时的长为.
14. 已知m是一元二次方程的一个根,则的值是.15. 小颖将能够活动的菱形学具活动成为图1所示形状,并测得 , .接着,她又将这个学其活动成为图2所示正方形,此时的长为. 16. 如图,已知点 , 分别在反比例函数和的图象上,以 , 为邻边作▱ , 点恰好落在轴上,且边交函数图象于点 , 当时,则 .
16. 如图,已知点 , 分别在反比例函数和的图象上,以 , 为邻边作▱ , 点恰好落在轴上,且边交函数图象于点 , 当时,则 .
三、解答题(共8题,共46分)
-
17. 计算:(1)、 ;(2)、18. 解方程:(1)、x(2x-5)=2x-5;(2)、 .19. 入为响应习近平提出的“绿水青山就是金山银山”的重要思想某校举办了“绿水青山,生态文明”知识竞赛(竞每一项的满分10分,学生得分均为整数).在这次竞赛中张山与李仕两位同学表现优秀,他们的四项成绩分布的条形统计图如图所示根据上图结果解答下列问题。
 (1)、补充完成下表
(1)、补充完成下表姓名
平均成绩(分)
中位数(分)
众数(分)
方差(分2)
张山
9
9
李仕
9.5
1.5
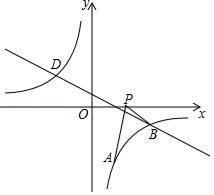
(2)、根据(1)题数据,分别从中位数、方差两个角度比较说明两位同学的各自优势?(3)、若实践操作、环保论文、现场抢答、笔试得分技4:1:2:3的比例折合成综合得分,请通过计算说明哪位同学的综合得分更高。20. 现代互联网技术的广泛应用,催生了快递行业的高速发展,据调查,某快递公司今年九月份与十一月份的投递总件数分别为10万件和12.1万件,该公司每月的投递总件数的增长率相同.求该快递公司投递总件数的月增长率.21. 如图所示,矩形AOBC的边AO,OB在两坐标轴上,双曲线 与矩形AOBC的边交于点D,E,点C(8,5),求D,E两点的坐标.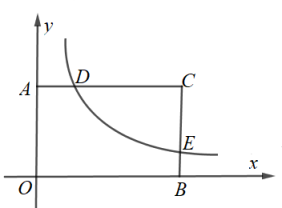 22. 如图,已知点A(1,a)是反比例函数y1= 的图象上一点,直线y2=﹣ 与反比例函数y1= 的图象的交点为点B、D , 且B(3,﹣1),求:
22. 如图,已知点A(1,a)是反比例函数y1= 的图象上一点,直线y2=﹣ 与反比例函数y1= 的图象的交点为点B、D , 且B(3,﹣1),求:(Ⅰ)求反比例函数的解析式;
(Ⅱ)求点D坐标,并直接写出y1>y2时x的取值范围;
(Ⅲ)动点P(x , 0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.