沪科版数学八年级下学期复习——平行四边形的五种判定专题练习
试卷更新日期:2023-05-17 类型:同步测试
一、一组对边平行且相等
-
1. 下面关于平行四边形的说法中,错误的是( )A、对角线互相平分的四边形是平行四边形 B、有一组对边平行,另一组对边相等的四边形是平行四边形 C、两组对边分别相等的四边形是平行四边形 D、有两组对角相等的四边形是平行四边形2. 如图.点B,E,C,F在同一条直线上, , 连接AD.求证:
 (1)、:(2)、四边形ABED是平行四边形.3. 已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.
(1)、:(2)、四边形ABED是平行四边形.3. 已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE. (1)、求证:△AFD≌△CEB.(2)、求证:四边形ABCD是平行四边形.4. 已知在△ABC中,AB=AC,点D在BC上,以AD、AE为腰做等腰三角形ADE,且∠ADE=∠ABC,连接CE,过E作EM∥BC交CA延长线于M,连接BM.
(1)、求证:△AFD≌△CEB.(2)、求证:四边形ABCD是平行四边形.4. 已知在△ABC中,AB=AC,点D在BC上,以AD、AE为腰做等腰三角形ADE,且∠ADE=∠ABC,连接CE,过E作EM∥BC交CA延长线于M,连接BM. (1)、求证:△BAD≌△CAE;(2)、若∠ABC=30°,求∠MEC的度数;(3)、求证:四边形MBDE是平行四边形.5. 如图,分别以的直角边及斜边向外作等边 , 等边 , 已知 , , 垂足为F,连接
(1)、求证:△BAD≌△CAE;(2)、若∠ABC=30°,求∠MEC的度数;(3)、求证:四边形MBDE是平行四边形.5. 如图,分别以的直角边及斜边向外作等边 , 等边 , 已知 , , 垂足为F,连接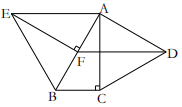 (1)、求证:;(2)、四边形是平行四边形吗?请说明理由.6. 如图,在▱ABCD中,点E在边AD上,连接EB并延长至F,使BF=BE;连接EC并延长至G,使CG=CE,连接FG,点H为FG的中点,连接DH,AF.
(1)、求证:;(2)、四边形是平行四边形吗?请说明理由.6. 如图,在▱ABCD中,点E在边AD上,连接EB并延长至F,使BF=BE;连接EC并延长至G,使CG=CE,连接FG,点H为FG的中点,连接DH,AF. (1)、若∠BAE=70°,∠DCE=20°,求∠DEC的度数;(2)、求证:四边形AFHD为平行四边形.7. 如图,在四边形中,点 , , , 分别为边 , , , 的中点.
(1)、若∠BAE=70°,∠DCE=20°,求∠DEC的度数;(2)、求证:四边形AFHD为平行四边形.7. 如图,在四边形中,点 , , , 分别为边 , , , 的中点. (1)、求证:四边形是平行四边形.(2)、若四边形的对角线互相垂直且它们的乘积为48,求四边形的面积.
(1)、求证:四边形是平行四边形.(2)、若四边形的对角线互相垂直且它们的乘积为48,求四边形的面积.二、两组对边分别平行
-
8. 如图,中,点 , 分别是边 , 的中点,过点作交的延长线于点 , 连结 .
 (1)、求证:四边形是平行四边形.(2)、当时,若 , , 求的长.9. 如图,是等边三角形,是射线上的一个动点(点不与 , 重合),是以为边的等边三角形,过点作的平行线交射线于点 , 连接 .
(1)、求证:四边形是平行四边形.(2)、当时,若 , , 求的长.9. 如图,是等边三角形,是射线上的一个动点(点不与 , 重合),是以为边的等边三角形,过点作的平行线交射线于点 , 连接 . (1)、如图1,点在线段上时,求证:;(2)、请判断图1中四边形的形状,并说明理由;(3)、若点在边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
(1)、如图1,点在线段上时,求证:;(2)、请判断图1中四边形的形状,并说明理由;(3)、若点在边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.三、两组对边分别对应相等
-
10. 已知:如图,在四边形ABCD中, ,对角线AC、BD相交于点O,且O是AC的中点.
 (1)、求证: ≌ ;(2)、求证:四边形ABCD是平行四边形.11. 如图,E,F是四边形ABCD的对角线AC上两点,AE=CF,DF=BE,DF∥BE.
(1)、求证: ≌ ;(2)、求证:四边形ABCD是平行四边形.11. 如图,E,F是四边形ABCD的对角线AC上两点,AE=CF,DF=BE,DF∥BE.

求证:
(1)、△AFD≌△CEB.;(2)、四边形ABCD是平行四边形.四、两组对角分别相等
-
12. 在下列给出的条件中,不能判定四边形ABCD为平行四边形的是( )A、 B、 C、 , D、13. 的比值中,能判断四边形ABCD是平行四边形的是( )A、 B、 C、 D、14. 如图,四边形的对角线、交于点 , 下列条件不能判定四边形为平行四边形的是( )
 A、 , B、 , C、 , D、 ,15. 下列条件中,不能判断四边形ABCD是平行四边形的是( )A、AB=CD,AD∥BC B、∠A=∠C,∠A+∠B=180° C、AD=BC,AD∥BC D、∠A=∠C,∠B=∠D16. 如图,四边形的对角线交于点O,下列哪组条件能判断四边形是平行四边形( )
A、 , B、 , C、 , D、 ,15. 下列条件中,不能判断四边形ABCD是平行四边形的是( )A、AB=CD,AD∥BC B、∠A=∠C,∠A+∠B=180° C、AD=BC,AD∥BC D、∠A=∠C,∠B=∠D16. 如图,四边形的对角线交于点O,下列哪组条件能判断四边形是平行四边形( ) A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 ,五、对角线互相平分
-
17. 如图,▱ABCD的对角线AC,BD相交于点O,E,F分别是OB,OD的中点,连接AE,AF,CE,CF.
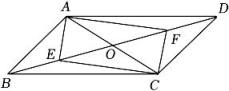 (1)、求证:四边形AECF是平行四边形;(2)、若AB⊥AC,AB=3,BC=5.
(1)、求证:四边形AECF是平行四边形;(2)、若AB⊥AC,AB=3,BC=5.①求AC的长;
②求BD的长.
18. 如图,在▱中,点、分别在、上,与相交于点 , 且.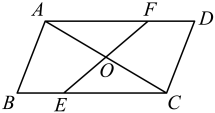 (1)、求证:≌;(2)、连接 , , 求证:四边形是平行四边形.19. 如图,四边形 中,对角线 , 相交于点O,点E,F分别在线段 , 上,且 . , .
(1)、求证:≌;(2)、连接 , , 求证:四边形是平行四边形.19. 如图,四边形 中,对角线 , 相交于点O,点E,F分别在线段 , 上,且 . , . (1)、证明: ;(2)、证明:四边形 是平行四边形.
(1)、证明: ;(2)、证明:四边形 是平行四边形.六、平行四边形存在性问题
-
20. 如图在10×10的正方形网格中,△ABC 的顶点在边长为1的小正方形的顶点上.
 (1)、计算AC,AB,BC的长度,并判定△ABC 的形状;(2)、若在网格所在的坐标平面内的点A,C的坐标分别为(0,0),(-1,1).请你在图中找出点D,使以A、B、C、D四个点为顶点的四边形是平行四边形,直接写出满足条件的D点的坐标.21. 如图所示,在四边形ABCD中,AD∥BC,BC=6厘米,AD=9厘米,P,Q分别从点A,C同时出发,点P以1厘米/秒的速度由点A向点D运动,点Q以2厘米/秒的速度由点C向点B运动。
(1)、计算AC,AB,BC的长度,并判定△ABC 的形状;(2)、若在网格所在的坐标平面内的点A,C的坐标分别为(0,0),(-1,1).请你在图中找出点D,使以A、B、C、D四个点为顶点的四边形是平行四边形,直接写出满足条件的D点的坐标.21. 如图所示,在四边形ABCD中,AD∥BC,BC=6厘米,AD=9厘米,P,Q分别从点A,C同时出发,点P以1厘米/秒的速度由点A向点D运动,点Q以2厘米/秒的速度由点C向点B运动。 (1)、几秒时四边形ABQP为平行四边形?(2)、几秒时直线PQ将四边形ABCD截出一个平行四边形?22. 如图,在平面直角坐标系xOy中,直线 与x轴,y轴分别交于点A,B,点C的坐标是 .
(1)、几秒时四边形ABQP为平行四边形?(2)、几秒时直线PQ将四边形ABCD截出一个平行四边形?22. 如图,在平面直角坐标系xOy中,直线 与x轴,y轴分别交于点A,B,点C的坐标是 . (1)、求 的度数;(2)、若第一象限内存在点D,使四边形ABCD是平行四边形,求点D的坐标.
(1)、求 的度数;(2)、若第一象限内存在点D,使四边形ABCD是平行四边形,求点D的坐标.

