吉林省长春市南关区2023年中考二模数学试题
试卷更新日期:2023-05-17 类型:中考模拟
一、单选题
-
1. 下列四个实数中,最小的数是( )A、 B、 C、0 D、2. 中国互联网络信息中心近期发布第51次《中国互联网络发展状况统计报告》显示,截止到2022年12月,我国网民规模达10.67亿.将数据10.67亿用科学记数法表示为( )A、 B、 C、 D、3. 如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )
 A、
A、 B、
B、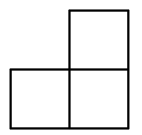 C、
C、 D、
D、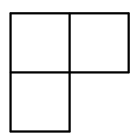 4. 不等式组的解集为( )A、 B、 C、 D、5. 如图,某停车场入口的栏杆 , 从水平位置绕点O旋转到的位置,已知的长为6米.若栏杆的旋转角 , 则栏杆A端升高的高度为( )
4. 不等式组的解集为( )A、 B、 C、 D、5. 如图,某停车场入口的栏杆 , 从水平位置绕点O旋转到的位置,已知的长为6米.若栏杆的旋转角 , 则栏杆A端升高的高度为( ) A、米 B、米 C、米 D、米6. 如图,四边形的两边、与相切于A、C两点,点B在上,若 , 则的度数为( )
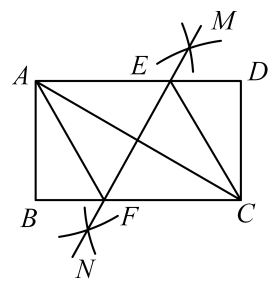
A、米 B、米 C、米 D、米6. 如图,四边形的两边、与相切于A、C两点,点B在上,若 , 则的度数为( ) A、 B、 C、 D、7. 如图,在矩形中, , 连接 , 分别以点A,C为圆心,大于的长为半径画弧,两弧交于点M、N,直线分别交于点E、F、下列说法不一定正确的是( )
A、 B、 C、 D、7. 如图,在矩形中, , 连接 , 分别以点A,C为圆心,大于的长为半径画弧,两弧交于点M、N,直线分别交于点E、F、下列说法不一定正确的是( )
 A、 B、 C、 D、8. 如图,在平面直角坐标系中,点 , , 将向右平移到位置,点A、O的对应点分别是C、E,函数的图象经过点C和的中点F,则k的值是( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,点 , , 将向右平移到位置,点A、O的对应点分别是C、E,函数的图象经过点C和的中点F,则k的值是( )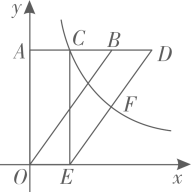 A、6 B、12 C、15 D、30
A、6 B、12 C、15 D、30二、填空题
-
9. 分解因式: =.10. 关于x的一元二次方程无实数解,则k的取值范围是 .11. 将一副三角板按如图所示的方式摆放,点D在边上,点E在边的延长线上, , , 则的大小为度.
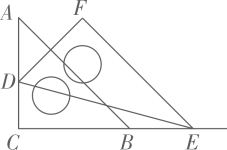 12. 如图,用一个半径为的定滑轮拉动重物上升,滑轮旋转了 , 假设绳索粗细不计,且与轮滑之间没有滑动,则重物上升了 . (结果保留)
12. 如图,用一个半径为的定滑轮拉动重物上升,滑轮旋转了 , 假设绳索粗细不计,且与轮滑之间没有滑动,则重物上升了 . (结果保留) 13. 如图,点O为正六边形对角线上一点,阴影部分的面积和为 , 则正六边形的边长是 .
13. 如图,点O为正六边形对角线上一点,阴影部分的面积和为 , 则正六边形的边长是 . 14. 如图,在平面直角坐标系中,O为坐标原点,点C为y轴正半轴上的任意一点,过点C的直线与二次函数的图象交于A、B两点,点A的横坐标为 , 且 , P为的中点,过点P作x轴的平行线分别交抛物线于M、N两点,则的长为 .
14. 如图,在平面直角坐标系中,O为坐标原点,点C为y轴正半轴上的任意一点,过点C的直线与二次函数的图象交于A、B两点,点A的横坐标为 , 且 , P为的中点,过点P作x轴的平行线分别交抛物线于M、N两点,则的长为 .
三、解答题
-
15. 先化简,再求值: , 其中 .16. 在三张形状、大小、质地均相同的卡片上各写一个数字,分别为、、 . 现将三张卡片放入一只不透明的盒子中,搅匀后任意抽出一张,记下数字后放回,搅匀后再任意抽出一张记下数字.用画树状图(或列表)的方法,求两次抽出的卡片上数字为一正一负的概率.17. 疫情过后,今年云南旅游市场强劲复苏.某旅行社今年春节租用A、B两种客房,用元租到A客房的数量与用元租到B客房的数量相同,今年每间A客房的租金比每间B客房的租金多元,分别求今年该旅行社租用的A、B两种客房每间客房的租金.18. 如图,在的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形.图中为格点三角形,只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
 (1)、在图①中,作出边的中线;(2)、在图②中,作出过A、B、C三点的所有格点平行四边形;(3)、在图③中,作出与相似的所有格点三角形,要求所作格点三角形与有两边分别共线,且所作格点三角形与的相似比为2:1.19. 在中, , D是的中点,E是的中点,过点A作交的延长线于点F.
(1)、在图①中,作出边的中线;(2)、在图②中,作出过A、B、C三点的所有格点平行四边形;(3)、在图③中,作出与相似的所有格点三角形,要求所作格点三角形与有两边分别共线,且所作格点三角形与的相似比为2:1.19. 在中, , D是的中点,E是的中点,过点A作交的延长线于点F. (1)、求证:四边形是菱形;(2)、若 , , 求菱形的面积.20. 年国家统计局公布了《年国民经济和社会发展统计公报》.公报显示,全国年至2022年货物进出口额变化情况,根据国家统计局年发布的相关信息,绘制了如下的统计图,请利用统计图中提供的信息回答下列问题:
(1)、求证:四边形是菱形;(2)、若 , , 求菱形的面积.20. 年国家统计局公布了《年国民经济和社会发展统计公报》.公报显示,全国年至2022年货物进出口额变化情况,根据国家统计局年发布的相关信息,绘制了如下的统计图,请利用统计图中提供的信息回答下列问题: (1)、从年到年,进口额最多的是年;(2)、从年到年,出口额年增长率的中位数是;(3)、货物进出口差额是衡量国家经济的重要指标,货物出口额超过货物进口额的差额称为货物进出口顺差,年我国货物进出口顺差是万亿元;(4)、下列结论正确的是 . (只填序号)
(1)、从年到年,进口额最多的是年;(2)、从年到年,出口额年增长率的中位数是;(3)、货物进出口差额是衡量国家经济的重要指标,货物出口额超过货物进口额的差额称为货物进出口顺差,年我国货物进出口顺差是万亿元;(4)、下列结论正确的是 . (只填序号)①与年相比,年的进口额的年增长率虽然下降,但进口额仍然上升.
②年进口额增长率持续下降.
③与年相比,年出口额增加了万亿元,出口额年增长率下降了个百分点;(注:为1个百分点)
21. 现有一批游客分别乘坐甲、乙两辆旅游车同时从旅行社前往某个旅游景点.行驶过程中甲车因故停留一段时间后继续驶向景点,乙车全程以的速度匀速驶向景点.两辆车的行驶路程与时间之间的函数关系如图所示. (1)、甲车停留前行驶时的速度是 , h;(2)、求甲车停留后继续行驶时的行驶路程y与时间x之间的函数关系式;(3)、求甲车比乙车早多少时间到达旅游景点?22. 实践与探究(1)、操作一:如图①,对折矩形纸片 , 使与重合,折痕为 . 把纸片展平后,将矩形纸片沿过点D的直线折叠,使点A落在上,点A的对应点为点 , 折痕为 , 连结 .
(1)、甲车停留前行驶时的速度是 , h;(2)、求甲车停留后继续行驶时的行驶路程y与时间x之间的函数关系式;(3)、求甲车比乙车早多少时间到达旅游景点?22. 实践与探究(1)、操作一:如图①,对折矩形纸片 , 使与重合,折痕为 . 把纸片展平后,将矩形纸片沿过点D的直线折叠,使点A落在上,点A的对应点为点 , 折痕为 , 连结 .
①当矩形是正方形时,是 ▲ 三角形;
②当是等腰直角三角形时,求边与边之间的数量关系;
③若点P、、C共线,求证: .
(2)、操作二:如图②,在矩形中, , . 先将矩形纸片沿过点D的直线折叠,使点A落在矩形的内部,点A的对应点为点 , 折痕为 . 然后沿过点D的直线折叠,使点C落在直线上,折痕为 , 点C的对应点为点 . 再将矩形沿过点G的直线继续折叠,折痕为 , 点B的对应点为点 . 我们发现,点H的位置不同,点B的位置也不同.当点恰好与点 . 重合时,线段的长为 . 23. 如图①,在中, , , . 动点P从点A出发,在上以每秒5个单位长度的速度向终点B运动,同时动点Q从点B出发沿折线以每秒7个单位长度的速度向终点A运动,当点Q不与点C重合时,以、为邻边作平行四边形 . 设点P的运动时间为t秒.
23. 如图①,在中, , , . 动点P从点A出发,在上以每秒5个单位长度的速度向终点B运动,同时动点Q从点B出发沿折线以每秒7个单位长度的速度向终点A运动,当点Q不与点C重合时,以、为邻边作平行四边形 . 设点P的运动时间为t秒. (1)、用含t的代数式表示线段的长;(2)、当点E在内部时,求t的取值范围;(3)、当的边将平行四边形的面积分为1:2两部分时,求t的值;(4)、如图②,点D为的中点,连接 , 作点C关于直线的对称点 , 当时,直接写出的值.24. 在平面直角坐标系中,抛物线(b、c为常数)的对称轴为直线 , 且经过点 . 点P在该抛物线上,其横坐标为m.(1)、求此抛物线对应的函数表达式;(2)、当时,求函数y的最大值和最小值;(3)、将此抛物线上P、A两点之间的部分(包括P、A两点)记为图象G,当图象G与直线只有一个公共点时,求m的取值范围;(4)、设点Q的坐标为 , 当不与坐标轴平行时,以为对角线构造矩形 , 且轴.当拋物线与矩形的边只有两个交点,且交点的纵坐标之差为时,直接写出m的值
(1)、用含t的代数式表示线段的长;(2)、当点E在内部时,求t的取值范围;(3)、当的边将平行四边形的面积分为1:2两部分时,求t的值;(4)、如图②,点D为的中点,连接 , 作点C关于直线的对称点 , 当时,直接写出的值.24. 在平面直角坐标系中,抛物线(b、c为常数)的对称轴为直线 , 且经过点 . 点P在该抛物线上,其横坐标为m.(1)、求此抛物线对应的函数表达式;(2)、当时,求函数y的最大值和最小值;(3)、将此抛物线上P、A两点之间的部分(包括P、A两点)记为图象G,当图象G与直线只有一个公共点时,求m的取值范围;(4)、设点Q的坐标为 , 当不与坐标轴平行时,以为对角线构造矩形 , 且轴.当拋物线与矩形的边只有两个交点,且交点的纵坐标之差为时,直接写出m的值